移动谐振荷载作用下曲线轨道钢轨动力响应求解方法研究

杜林林，刘维宁，刘卫丰，马龙祥

(1.北京交通大学 土木建筑工程学院，北京 100044；2.西南交通大学 土木工程学院，成都 610031)

曲线轨道能够适应地形、地物、地质等条件的约束，满足城市轨道交通线路的规划设计要求[1]。然而列车通过曲线轨道时产生的振动问题却不容忽视，以北京地铁为例，曲线轨道处出现了大量的异常波磨，影响车辆运行甚至危及行车安全[2]，曲线段列车运行引起的地表振动响应较大[3]。不同于直线轨道，列车在曲线轨道运行时会引起曲线轨道的平面内振动以及平面外振动，对于列车运行时的垂向荷载来说，平面外振动占主要成分[4-5]，为研究列车通过曲线轨道过程中的轮轨相互作用关系，应首先明确移动荷载作用下曲线轨道的动力响应特性，因此本文首先开展移动简谐荷载作用下曲线轨道弯扭耦合振动特性的研究。

针对曲线梁振动特性的研究，姚玲森[6]根据Vlasov[7]曲线梁平衡方程，采用傅里叶级数法求解简支曲线梁内力，通过求解两个联立的四阶微分方程得到曲梁的内力和变形。单德山[8]应用积分变换法，求解了移动荷载作用下简支曲线梁弯扭耦合振动的解析解，并进一步研究了高速铁路曲线梁桥车桥耦合振动。宋郁民等[9]运用模态叠加法，通过考虑列车曲线的通过特点及轮轨非线性相互作用，建立了空间列车-桥梁的耦合方程。Yang等[10]通过模态叠加法，研究了水平曲线简支梁在竖向力和水平力的共同作用下，曲线梁的弯扭耦合振动响应。刘维宁等[11]根据曲线梁的传递矩阵，以Duhamel积分为基础，推导了移动荷载作用下周期性离散支承的曲线Timoshenko梁平面外振动响应的解析解。总体来说，针对曲线梁振动特性的研究相对较少，而对于移动荷载作用下周期性离散支承的曲线轨道动力响应问题仍需作进一步的研究。

考虑到轨道结构离散支承的周期性特点，部分学者采用周期性结构理论对轨道结构的动力学响应进行分析，如马龙祥等[12]在Belotserkovskiy[13]的基础上，采用周期性结构理论给出了直线轨道结构动力响应的频域解析求解方法，具有求解高频响应效率高的优势。但以往采用此方法的研究多是集中于直线轨道，本文将采用周期性结构理论对曲线轨道动力响应的求解方法进行研究。

本文利用轨道结构周期性条件，在一个基本元内对曲线轨道钢轨动力响应问题开展研究。通过引入单位移动谐振荷载作用下曲线轨道钢轨的数学模态，得出了曲线轨道钢轨频域响应的级数表达。在频域内采用模态叠加法表示钢轨的弯曲及扭转变形，进而求解得出钢轨的频域动力响应，得到了移动荷载作用下曲线轨道平面外弯扭耦合振动的响应特性。不同于曲线轮-轨动态耦合研究，曲线超高、轮轨间横向相互作用力及轨底坡等对轮轨动态相互作用影响较大，本文主要研究移动简谐荷载作用下曲线轨道的振动响应问题，可以忽略超高、横向轮轨力、轨底坡等因素的影响，将曲线轨道简化为周期性离散支承的平面曲线梁。最终，本文将给出移动谐振荷载作用下曲线轨道动力响应的求解方法，该方法具有力学概念清晰、没有截断误差、求解效率高等优点。基于该方法，本文将对曲线轨道的动力响应特性进行分析。

1 移动谐振荷载作用下周期性结构响应特点

周期结构是指在空间上具有周期性的结构，且任意周期范围可称作结构的基本元。由于振动波在周期结构内具有特殊的性质，研究人员提出了周期-无限结构理论。无限-周期轨道结构在竖向移动谐振荷载作用下，当荷载激励点移动一个周期长度后，无限-周期轨道结构的受力情况只是荷载随着时间的变化增加了一个相位。本文将曲线轨道映射至圆形轨道结构中，根据周期性结构的性质对曲线轨道的动力特性进行分析，如图1所示。通过求解移动谐振荷载沿圆周作用下轨道结构的动力响应，可得列车在曲线轨道上运行引起的轨道弯扭耦合动力响应[14-15]。

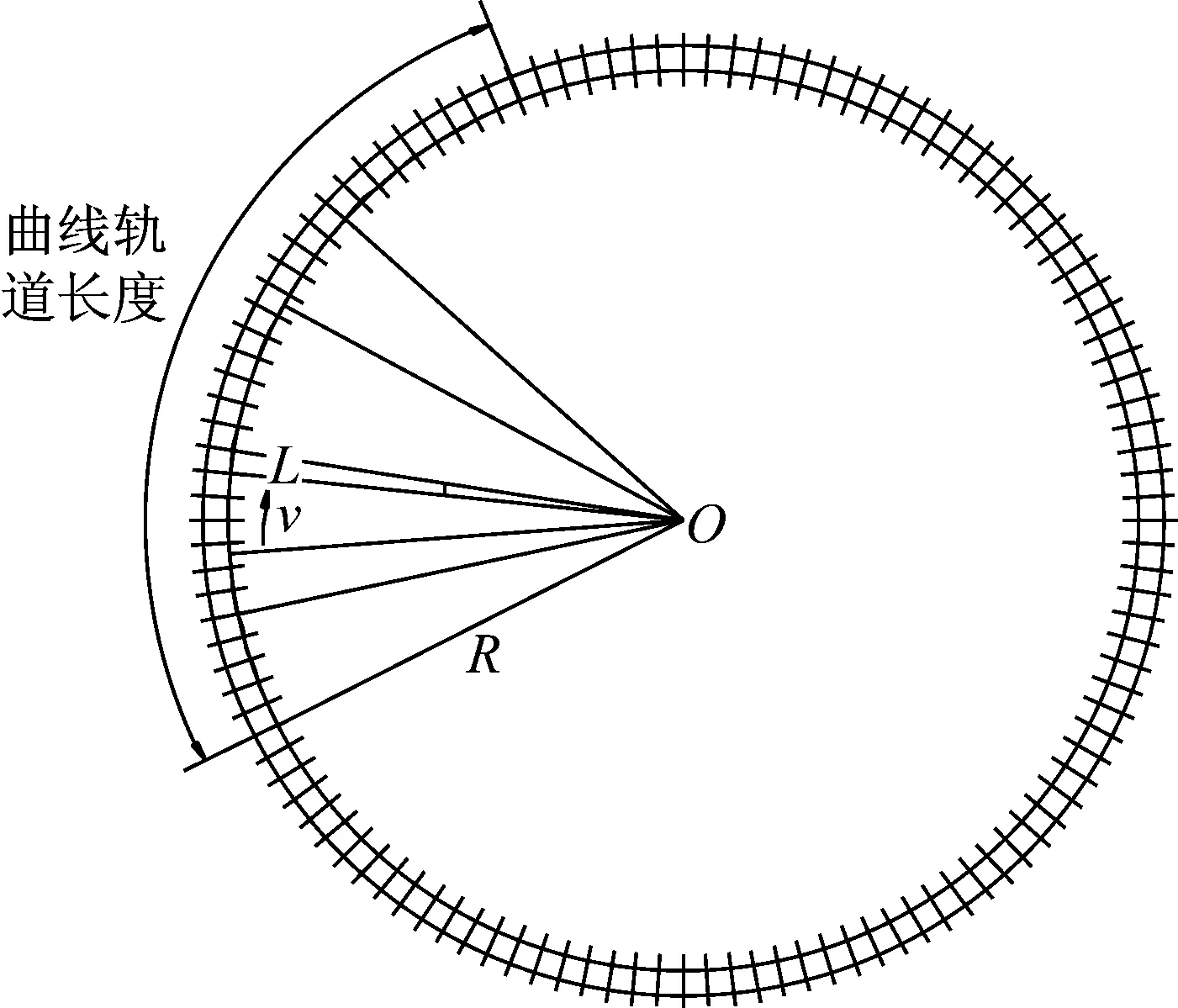
图1 曲线轨道周期性Fig.1 Periodic property of curved track

1.1 移动荷载作用下曲线轨道的周期性

如图1所示，曲线轨道半径为R，扣件间距为L，荷载移动速度为v，由结构振动特性可知

h(z1,z2,t)=h(z1+L,z2+L,t)

(1)

式中:h(z1,z2,t)为结构的脉冲响应函数，即在z2位置作用竖向的单位脉冲荷载，引起z1处时刻t的竖向位移响应；L为结构的周期长度。

根据Duhamel定理，曲线轨道任意拾振点z处的竖向位移响应为

(2)

(3)

根据式(1)和式(3)有

u(z+L,t+L/v)=

eiωFL/v·u(z,t)

(4)

至此，可以发现无限-周期轨道结构在竖向移动谐振荷载FeiωFt作用下，当荷载激励点z=vt(v为荷载移动角速度)移动一个周期长度L后，无限-周期轨道结构的受力情况将与时刻t时的相仿，只是荷载随着时间的变化增加了一个相位ωFL/v。

对式(4)关于时间t作傅里叶变换，可得周期-无限结构动力响应关系在频域里的表达

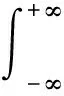
(5)

式中:ω为角频率；符号“∧”代表频域内的物理量。

1.2 曲线轨道钢轨频域响应的模态叠加法

移动谐振荷载作用下钢轨动力响应具有如下周期性性质

(6)

(7)

结合式(6)与式(7)，有：

(8)

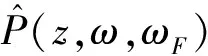
(9)

式中:Cn(ω,ωF)是傅里叶级数系数；ξn=2πn/L。

(10)

记

(11)

(12)

(13)

式中：Un(ω,ωF)、Φn(ω,ωF)分别为频域内竖向位移、扭转变形各模态所对应的傅里叶级数系数。

(14)

(15)

式中:纳入考虑的钢轨模态数为2N+1，将其记为NMR，即NMR=2N+1。

根据周期-无限结构的性质，采用频域内曲线钢轨的数学模态叠加法，对移动谐振荷载作用下的曲线轨道钢轨动力响应进行求解。

2 曲线轨道动力响应分析

2.1 圆弧曲梁振动微分方程推导

在推导曲线梁振动微分方程时，假定曲线梁为等截面的匀质梁且曲率半径为常数，横截面具有竖直的对称轴；曲线梁形心与剪切中心重合；曲率半径远大于横截面、梁长和梁宽的尺寸。曲线梁的坐标系按照右手螺旋法则规定，如图2所示。

图2 曲线梁坐标系Fig.2 Coordinate of curved beam

自由振动下，忽略高阶微量，曲线梁的轴向、径向、垂向及扭转振动微分方程为[18-20]

(16)

(17)

(18)

(19)

式中:ux,uy,uz分别为x,y,z方向上的位移；φz为绕z轴的扭转变形；m为单位长度质量；ρ为密度；A为截面面积；Id为截面扭转常数；I0为截面极惯性矩；E,G分别为弹性模量和剪切模量；Ix,Iy分别为绕x,y轴的截面惯性矩；Iω为截面扭转翘曲常数；R为曲线半径。

由式(16)～(19)可知，式(16)和(17)表示曲梁的轴向及径向，即平面内振动微分方程，式(18)和(19)表示曲梁的垂向及扭转，即平面外振动微分方程。观察式(16)～(19)可知，曲线梁平面内振动与平面外振动相互独立，且曲梁平面内振动对平面外振动影响很小，因此，移动垂向荷载作用下曲线梁的动力响应仅考虑平面外振动情况。

考虑到曲线轨道半径远大于钢轨截面尺寸，钢轨动力变形中忽略翘曲Iω=0，移动荷载作用下曲线梁弯扭耦合振动响应为

(20)

(21)

2.2 曲线钢轨动力学控制方程

将钢轨简化为曲线Euler-Bernoulli梁，将扣件简化为弹簧阻尼支点，此时轨道简化为等间距离散点支承的轨道模型，令速度为v、角频率为ωF的单位谐振荷载eiωFt作用在曲线钢轨上，如图3所示。

图3 移动简谐荷载作用下曲线轨道力学模型Fig.3 Mechanics model of curved track subjected to harmonic moving loads

此时钢轨的控制方程可以写为

(22)

(23)

对式(22)、式(23)进行傅里叶变换

(24)

(25)

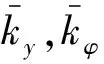
图4 钢轨变形及约束示意图Fig.4 Schematic of constraint of rail

(26)

(27)

对式(26)、(27)进行数学整理，则有

Gu=P

(28)

式中:u={U-N,…,U+N,Φ-N,…,Φ+N}T；G为NMR×2阶方阵；P为(NMR+NMR)×1阶向量，满足

(29)

在任一角频率下，解式(28)可得钢轨的各模态坐标，代入式(14)、(15)即可求得曲线轨道钢轨基本元内任意一点对应频率的位移响应。对于曲线轨道钢轨上其它点的动力响应，根据周期性结构响应的特性，利用式(5)扩展得到，有：

(30)

(31)

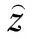
3 模型验证及曲线轨道振动特性分析

3.1 模型验证

文献[23]中给出了移动谐振荷载作用下离散支承的曲线轨道动力响应，并与本文计算结果进行了对比，以验证本文计算方法的正确性。文献[23]中的轨道参数如下：轨道模型长90 m，曲线轨道半径为20 m，单位长度钢轨质量为60.21 kg/m，钢轨横截面面积为7.672×10-3m2，弹性模量为210 GPa，泊松比为0.3，截面竖向抗弯惯性矩为3 038.3×10-8m4，截面自由扭转惯性矩，极惯性矩为3 550.6×10-8m4，钢轨材料损耗因子为0.01。扣件支承间距为0.6 m，刚度为20 MN/m，阻尼为2×104N·s/m。荷载移动速度为20 m/s，荷载幅值为1 N。

由图5可知，本文计算结果与文献[23]中的计算结果基本一致，验证了本文计算模型的正确性。

3.2 曲线轨道振动特性分析

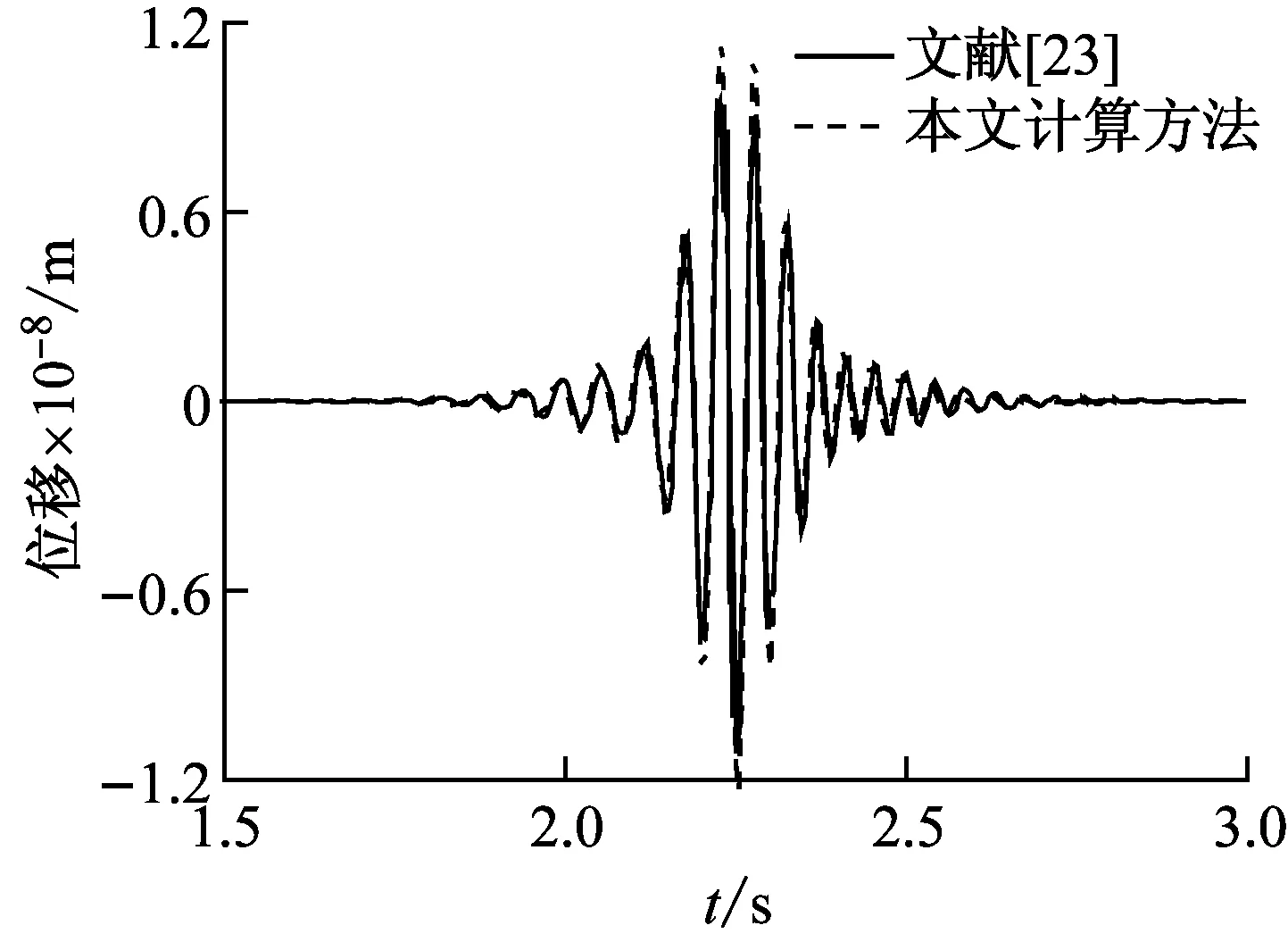
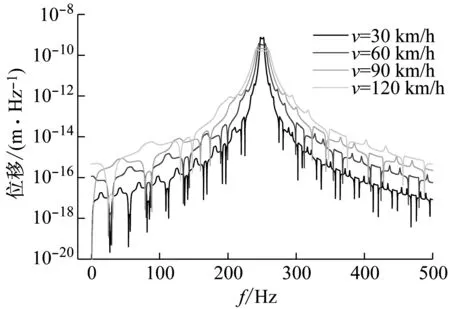
为了研究移动谐振荷载作用下曲线轨道的动力响应特性，本节以地铁普通整体道床DTVI2扣件轨道为例，研究曲线半径及荷载移动速度对曲线轨道动力响应的影响。图6给出了曲线轨道半径与扣件间距比值对垂向、扭转位移响应幅值的影响；图7给出了荷载移动速度分别为30 km/h、60 km/h、90 km/h、120 km/h时的曲线轨道动力响应的时程及频谱特点。为了对比采用曲梁模型模拟钢轨与采用直梁模型模拟曲线钢轨间的区别，图8给出了移动速度60 km/h时，半径为300的曲梁轨道模型与直梁轨道模型所得动力响应的对比结果。

DTVI2扣件及T60钢轨参数见表1，计算模态数取为81。荷载初始位置为0，荷载幅值为1 N，频率为250 Hz，拾振点在45 m处，曲线半径为300 m。

(a)激振频率为0 Hz时拾振点处位移响应

(b)激振频率为20 Hz时拾振点处位移响应

(a)垂向位移

(b)扭转角位移

(a)时程

(b)频谱

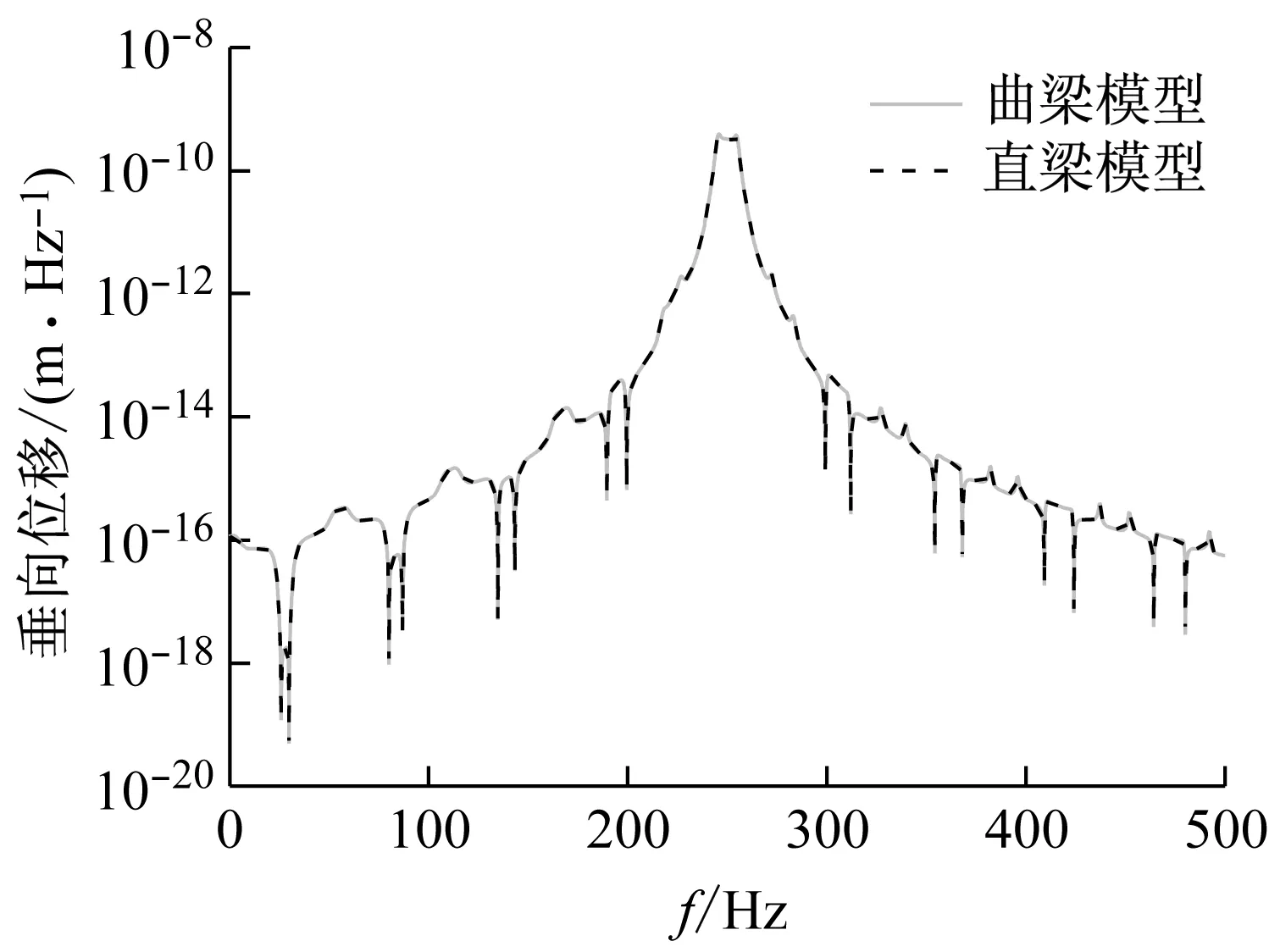
(a)垂向位移响应

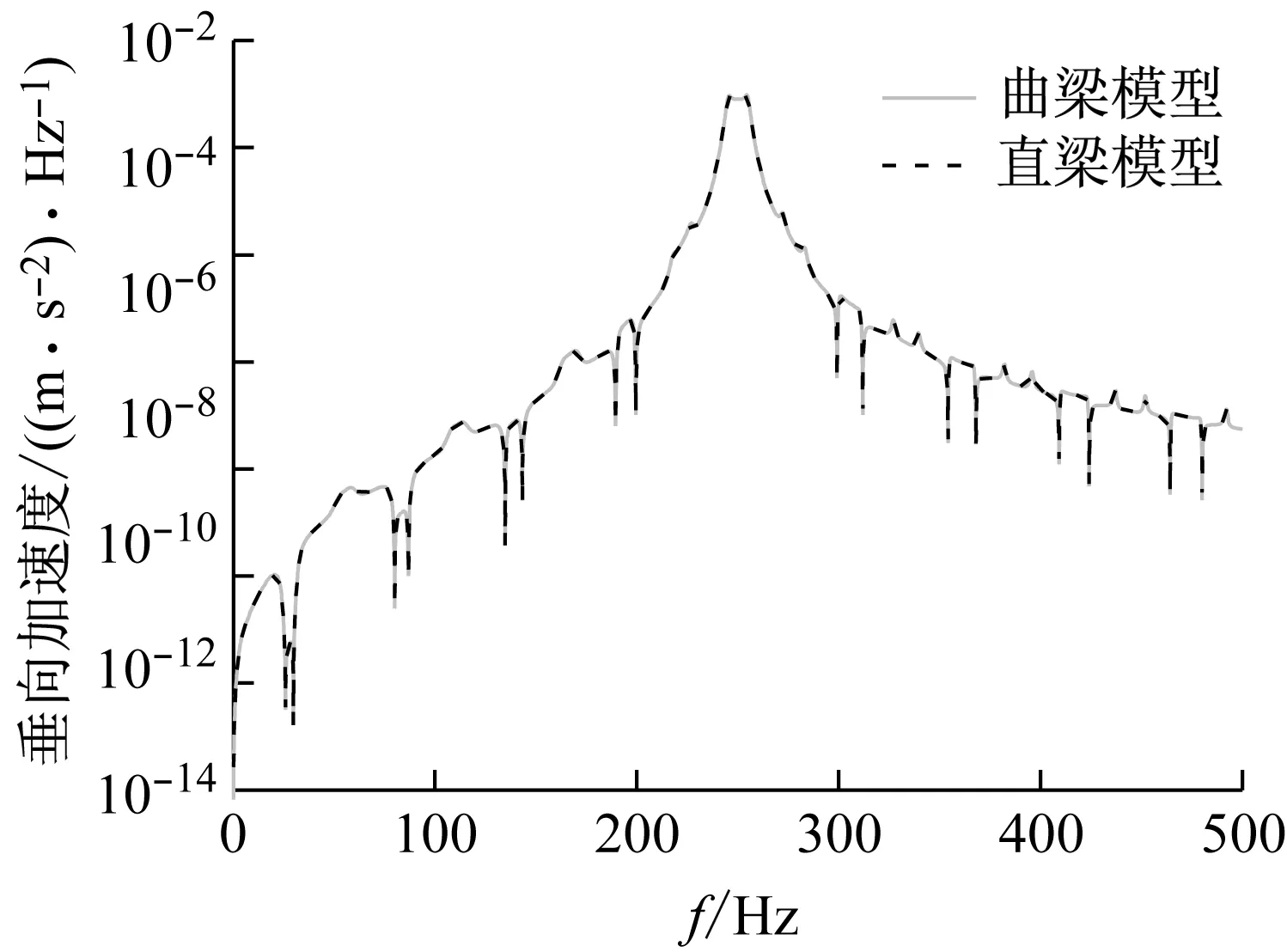
(b)垂向加速度响应

图8 移动谐振荷载下曲梁、直梁模拟曲线轨道钢轨动力响应对比
Fig.8 Comparison of dynamic response of curved track simulated by curved beam and straight beam

表1 DTVI2扣件轨道及T60钢轨参数Tab.1 Parameters of track with DTVI2 fasteners and T60 rail

由以上计算结果可知：

(1)由图6可知，垂向单位谐振移动荷载作用下，采用曲线梁模型模拟轨道时，钢轨垂向位移响应幅值随曲线半径的增大而变小，当半径与扣件支点间距比值在10以内时，半径对钢轨位移响应影响较大，当曲线半径较大时半径对钢轨位移响应的影响较小；钢轨扭转响应幅值随曲线半径的增大而变小，曲线半径对钢轨扭转角位移响应的影响较大；

(2)由图7可知在移动谐振荷载作用下，轨道响应显著的频段位于荷载激励频率附近；由于离散支承的影响，响应频谱在荷载频率两侧出现彼此间距为v/L的参数激励；随着荷载移动速度的增加，荷载激励频率附近一个很窄频段内的位移响应将有所减小，但其它大部分频段内的位移响应将显著增大，参数激励受荷载速度变化影响显著；

(3)随着荷载移动速度的增加，移动谐振荷载引起轨道响应在时程上的最大峰值变化不大，但响应显著的持续时间将变短。

(4)由图8可知，曲线轨道半径为300 m时，竖向移动谐振荷载作用下的钢轨垂向动力响应特性与直梁模型基本一致。

4 结 论

(1)本文将曲线轨道视作周期性轨道结构，在一个基本元内对钢轨动力响应进行研究，通过引入单位移动谐振荷载作用时钢轨的数学模态，给出了离散支承曲线轨道钢轨平面外振动响应的频域求解方法，该方法具有力学概念清晰准确、没有截断误差、求解高频响应效率高等优点。

(2)移动谐振荷载作用下，曲线轨道钢轨动力响应显著的频段位于荷载激励频率附近；随着速度的增加，荷载频率附近一个很窄频段内的位移响应有所减小，其它大部分频段内的位移响应显著增大。

(3)随着速度的增加，荷载引起的钢轨响应时程峰值变化不大，但响应时间显著变短；频域内由钢轨离散支承引起的参数激励受荷载速度变化影响显著。

(4)对于普通地铁曲线轨道来说，采用曲线梁模型模拟曲线轨道钢轨垂向动力响应所得结果与采用直梁模型所得结果基本一致，可以采用直梁模型近似研究曲线轨道垂向动力响应；考虑到曲线半径对曲线钢轨扭转振动响应有一定程度的影响，对轨道进行精细化建模分析时，需采用曲梁模型研究曲线轨道动力响应。