集合、函数、导数核心考点A卷参考答案

一、选择题

二、填空题

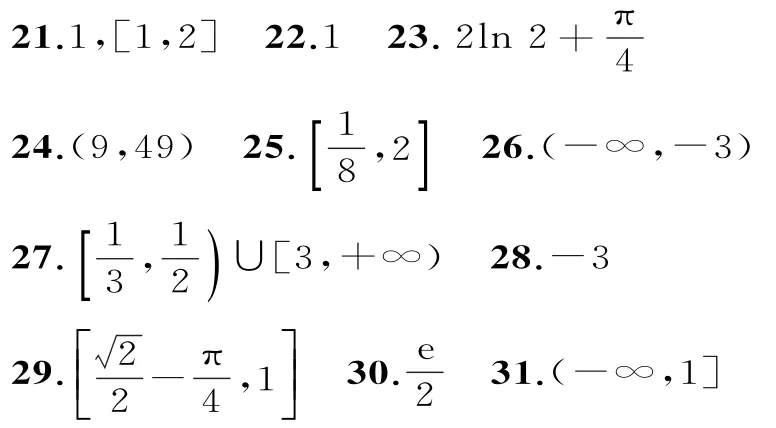
三、解答题

(2)A∩B=A,则A⊆B,A中不等式的解集分三种情况讨论:

①当a=0时,A=R,A⊆B不成立;

综上所述,a的取值范围是(-∞,-4)∪[2,+∞)。

3 3.(1)设t=l o g2x,t∈R,则x=2t。因为函数f(l o g2x)=x2+2x,所以f(t)=22t+2·2t,所以把t换成x可得f(x)=22x+2·2x。

(2)方程f(x)=a·2x-4在(0,2)内有两个不相等的实根⇒22x+(2-a)·2x+4=0,在(0,2)内有两个不等实根。令2x=m,则h(m)=m2+(2-a)m+4。

因为x∈(0,2),所以m∈(1,4)。所以函数h(m)在(1,4)上有两个不等实数根。

又6 0≤x≤1 2 0,可得6 0≤x≤1 0 0,每小时的油耗不超过9L,所以x的取值范围为[6 0,1 0 0]。

3 5.(1)由题意可知f(1)≥2,f(1)≤2,所以f(1)=2,所以a+b+c=2。

因为对任意实数x都有f(x)≥2x,即a x2+(b-2)x+c≥0恒成立,所以a+b+c=2,可知a=

所以f(-1)=a-b+c=4a-2的取值范围是(-2,0]。

(2)对任意x1,x2∈[-3,-1]都有|f(x1)-f(x2)|≤1等价于在[-3,-1]上的最大值与最小值之差M≤1,由(1)知,

据此分类讨论如下:

令f'(x)=0,得x=e1-a,故f(x)在(0,e1-a)上是增函数,在(e1-a,+∞)上是减函数。故f(x)极大值=f(e1-a)=ea-1;无极小值。

(2)①当e1-a＜e2,即a＞-1时,f(x)在(0,e1-a)上是增函数,在(e1-a,e2]上是减函数。所以f(x)max=f(e1-a)=ea-1;f(e-a)=a≤e2-2。

②当e1-a≥e2,即a≤-1时,f(x)在(0,e2]上是增函数,故函数f(x)的图像与函数g(x)=1的图像在区间(0,e2]上至多有一个公共点,故不满足。

综上,实数a的取值范围是(1,e2-2]。

3 7.(1)由题易知f'(x)=ex-2,切线的斜率k=f'(0)=1-2=-1。

因f(0)=e0-2×0-1=0,故f(x)在(0,f(0))处的切线方程为y=-x。

(2)由题易知g(x)=ex-2a x-a,则g'(x)=ex-2a。

当a≤0时,g'(x)＞0,所以g(x)在R上单调递增,不符合题意。

当a＞0时,令g'(x)=0,得x=l n2a,在(-∞,l n2a)上,g'(x)＜0,在(l n2a,+∞)上,g'(x)＞0,故g(x)在(-∞,l n2a)上单调递减,在(l n2a,+∞)上单调递增。

所以 g(x)极小值=g(l n2a)=2a-2al n2a-a=a-2al n2a。

因为g(x)有两个零点,所以g(x)极小值＜0,即a-2al n2a＜0。

3 8.(1)由题知f'(x)=2x(l nx-1)+x=2xl nx-x,所以f'(1)=-1。

又f(1)=-1,所以在点(1,f(1))处的切线方程为x+y=0。

(2)由于函数y=f(x)的定义域为(0,+∞),所以m f(x)+ex≥0⇒m x2(l nx-1)

令g(x)=m x(l nx-1),则g'(x)=ml nx,可得,当x∈(0,1)时,g'(x)＜0;当x∈(1,+∞)时,g'(x)＞0。所以g(x)min=g(1)=-m。

所以h(x)max=h(1)=-e,由-m≥-e得m≤e。

所以m的取值范围为(0,e]。

由k(1)=0知,当0＜x＜1时,k(x)＞0,从而f'(x)＞0,当x＞1时,k(x)＜0,从而f'(x)＜0。

综上可知,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞)。

现证明:对任意x＞0,g(x)＜1+e-2恒成立。

当x≥1时,由(1)知g(x)≤0＜1+e-2成立;

当0＜x＜1时,ex＞1,且由(1)知g(x)-x。

设F(x)=1-xl nx-x,x∈(0,1),则F'(x)=-(l nx+2)。

当x∈(0,e-2)时,F'(x)＞0;当x∈(e-2,1)时,F'(x)＜0。所以当x=e-2时,F(x)取得最大值F(e-2)=1+e-2。

所以g(x)＜F(x)≤1+e-2,即0＜x＜1时,g(x)＜1+e-2。

综上,对任意x＞0,g(x)＜1+e-2。 ①

令G(x)=ex-x-1(x＞0),则G'(x)=ex-1＞0恒成立,所以G(x)在(0,+∞)上递增,G(x)＞G(0)=0恒成立,即ex＞

(Ⅰ)当a＜0时,f'(x)＜0,故函数f(x)在(0,+∞)上单调递减。

综上所述:当a≤0时,函数f(x)在(0,+∞)上单调递减;当a＞0时,函数f(x)在调递增。

(Ⅱ)因为对任意m∈[1,e],直线PM的倾斜角都是钝角,所以对任意m∈[1,e],直f(m)＜1,即f(x)在区间[1,e]上的最大值令g(x)=a x2-2,x∈[1,e]。

(1)当a≤0时,由(Ⅰ)知f(x)在区间[1,e]上单调递减,所以f(x)的最大值为

因为x∈[e,e2],所以f(x1)≤f'(x2)+a成立⇒x∈[e,e2],[e,e2]上为减函数,则f(x)min=f(e2)=

①当-a≥0,即a≤0时,f'(x)≥0在[e,e2]上恒成立,因此f(x)在[e,e2]上为增的单调性和值域可知,存在唯一x0∈(e,e2),使得f'(x0)=0,且满足:当x∈[e,x0)时,f'(x)＜0,f(x)为减函数;当x∈(x0,e2)时,f'(x)＞0,f(x)为增函数。所以f(x)min不合题意,舍去。

②当-a＜0,即