集合、函数、导数核心考点B 卷

■河南省信阳市第二高级中学 肖 瑞

一、选择题

1.已知集合A={y|y=x},B={(x,y)|y=x2-3},则A∩B的子集个数为( )。

A.0 B.1 C.2 D.4

2.已知集合A={x∈N*|x2-4＜0},B={-2,-1,0,1,2},则A∩B=( )。

3.函数f(x)=x2+l n(e-x)l n(e+x)的图像大致为图1中的( )。

图1

4.已知函数f(x)=xl nx-x+2a,若函数y=f(x)与y=f(f(x))有相同的值域,则a的取值范围是( )。

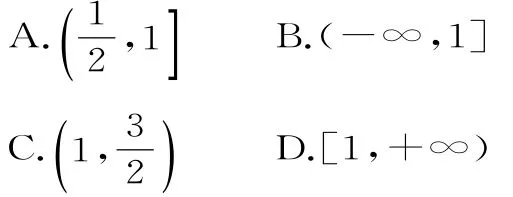
5.已知函数f(x)在R上存在导数f'(x),下列关于f(x),f'(x)的描述正确的是( )。

A.若f(x)为奇函数,则f'(x)必为奇函数

B.若f(x)为周期函数,则f'(x)必为周期函数

C.若f(x)不为周期函数,则f'(x)必不为周期函数

D.若f(x)为偶函数,则f'(x)必为偶函数

A.b＞c＞a B.a＞c＞b

C.b＞a＞c D.a＞b＞c

8.定义在R上的偶函数f(x)满足f(x+1)=-f(x),当x∈[0,1]时,(-1＜x＜3),则函数f(x)与g(x)的图像所有交点的横坐标之和为( )。

A.2 B.4 C.6 D.8

A.a＜b＜c B.b＜c＜a

C.c＜a＜b D.c＜b＜a

1 0.已知函数f(x)=l o ga(x2-3a x)对实数a的取值范围是( )。

1 1.若函数f(x)=2x+s i nx·c o sx+ac o sx在(-∞,+∞)上单调递增,则a的取值范围是( )。

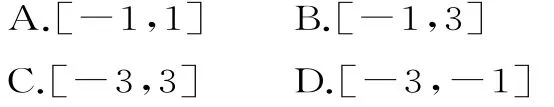
1 2.由曲线x y=1与直线y=x,y=3所围成的封闭图形的面积为( )。

1 3.若直线y=k x+1与曲线y=x3+a x+b相切于点A(1,3),则2a+b=( )。

A.8个 B.6个 C.4个 D.3个

15.已知k,b∈R,设直线l:y=k x+b是曲线y=ex+x的一条切线,则( )。

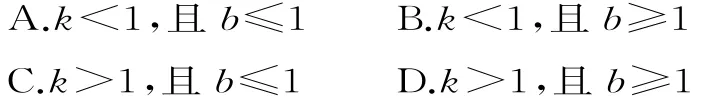
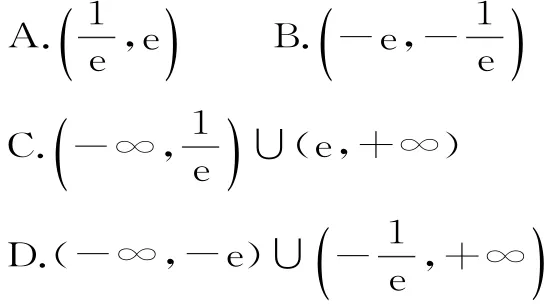
1 8.已知f(x)=x2ex,若函数g(x)=f2(x)-k f(x)+1恰有四个零点,则实数k的取值范围是( )。

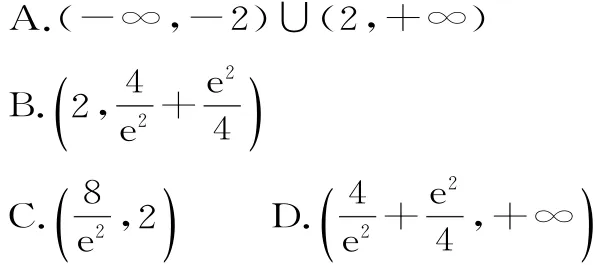
1 9.定义在R上的偶函数f(x)的导函数为f'(x),若对任意的实数x,都有2f(x)+x f'(x)＜2恒成立,则使x2f(x)-f(1)＜x2-1成立的实数x的取值范围为( )。

2 0.已知函数f(x)=x2+l n2x-2m·(x+l nx)+2m2+1,若存在x0使得f(x0)成立,则实数m的值为( )。

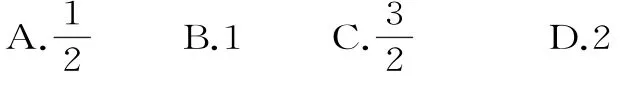
二、填空题

2 2.函数f(x)=2x+1-x的值域为____。

2 3.集合A={0,1,2},B={a,b},从集合A到集合B有____个不同的映射。

2 6.设f(x)是定义在R上以2为周期的偶函数,当x∈[0,1]时,f(x)=l o g2(x+1),则函数f(x)在[1,2]上的解析式是 。

2 8.已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,在(0,+∞)上单调递减,且f(4)=0,若f(x-3)≤0,则x的取值范围为____。

3 0.设函数f(x)在R上存在导函数f'(x),对任意的实数x都有f(x)=4x2-数m的取值范围是____。

3 2.设a＞0,函数f(x)=x+2(1-x)·s i n(a x),x∈(0,1),若函数y=2x-1与y=f(x)的图像有且仅有两个不同的公共点,则a的取值范围是____。

3 3.若存在正实数m,使得关于x的方程x-k(x+m-2 ex)[l n(x+m)-l nx]=0有两个不同的实根,其中e为自然对数的底数,则实数k的取值范围是____。

三、解答题

3 4.幂函数f(x)=(m-1)2xm2-4m+2在(0,+∞)上单调递增,函数g(x)=2x-k。

(1)求m的值;

(2)当x∈[1,2]时,记f(x),g(x)的值域分别为集合A,B,设命题p:x∈A,命题q:x∈B,若命题p是q成立的必要条件,求实数k的取值范围。

3 5.已知函数f(x)为二次函数,满足f(0)=1,且f(x+1)-f(x)=2x。

(1)求函数f(x)的解析式;

(2)若方程f(2x)=2x+a在x∈(-∞,2]上有两个不同的解,求实数a的取值范围。

3 6.由于渤海海域水污染严重,为了获得第一手的水文资料,潜水员需要潜入水深为6 0米的水底进行作业,根据经验,潜水员下潜的平均速度为v(米/单位时间),每单位时单位时间,每单位时间消耗氧气0.9(升),返位时间消耗氧气1.5(升),记该潜水员完成此次任务的消耗氧气总量为y(升)。

(1)求y关于v的函数关系式;

(2)若c≤v≤1 5(c＞0),求下潜速度v取什么值时,消耗氧气的总量最少。

3 7.设函数f(x)=[a x2-(4a+1)x+4a+3]ex。

(1)若曲线y=f(x)在点(1,f(1))处的切线与x轴平行,求a;

(2)若f(x)在x=2处取得极小值,求a的取值范围。

(1)求函数f(x)的单调区间;

3 9.已知函数f(x)=(2-a)(x-1)-2 l nx(a∈R)。

(1)若曲线g(x)=f(x)+x上点(1,g(1))处的切线过点(0,2),求函数g(x)的单调减区间;

4 0.已知函数f(x)=ex,g(x)=m x+n。

(1)设h(x)=f(x)-g(x),当n=0时,若函数h(x)在(-1,+∞)上没有零点,求m的取值范围;

(1)讨论函数f(x)的单调性;

(2)若函数f(x)有两个零点x1,x2(x1＜x2),且a=e2,证明:x1+x2＞2 e。