三轴超形变核174Hf组态的寻找

李晓伟

（赤峰学院 物理与电子信息工程学院，内蒙古 赤峰 024000）

1 引言

关于原子核形状的研究一直是核物理领域的重要主题，只有在幻数核的基态和低激发态才是球形的，而大多数原子核都是具有一定形变的.原子核三轴性研究是核物理的一个基本问题，它在很多核现象中起到很重要的作用.

例如，在实验上发现的反常旋称劈裂[1]、旋称反转[2]，手征二重带[3,4]等现象，它们都是由于原子核的质量在其三个轴向的分布不均而产生的原子核的奇异特性.对于原子核的三轴性，最早在20世纪70年代，就由Mottelson.B.R和Bohr.A在理论上预测到[5]，但是实验上，至到1992年才第一次在163Lu中发现原子核的三轴超形变带[6].随后，在Lu的很多同位素及该区域相邻元素的原子核中发现了多条三轴超形变带[7-11].最近的实验中，在174Hf中发现了四条三轴超形变带[12]，通过理论分析，应该是由于高j轨道的下倾，使N=100和N=106的区域形成新的壳能隙[12]，进而出现原子核的亚稳态.

对于174Hf三轴超形变带的三轴形变值和组态，本小组曾利用TRS方法，进行过理论计算，并确定了一个可能的组态和形变值[13]，但是基于一定的转动频率下的.由于核子空间组态的复杂性，本文将试图在较低转动频率下去寻找三轴形变带的组态，并分析不同组态下的准粒子能量对三轴形变的影响.

2 理论方法

在转动势场下，对于给定的准粒子组态的原子核的总能量是四极形变、三轴形变和十六极形变的函数，在一维推转近似下，体系总能量可以表示为：

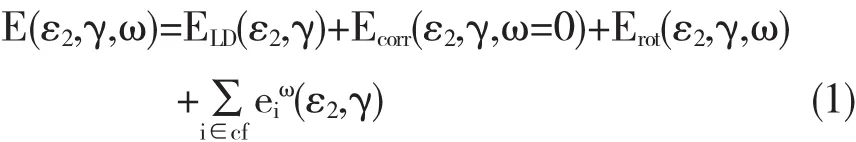
其中ELD为液滴能;Ecorr为壳修正和对修正能;Erot为集体转动能，是在真空态下哈密顿量在考虑转动和不考虑转动的情况下求出的能量差，

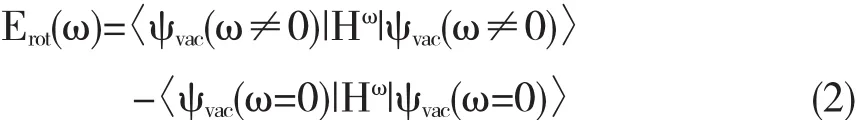
在势场绕X轴转动下，在其中运动的准粒子的哈密顿量为

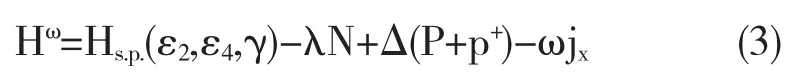
其中Hsp是静止势场中的粒子哈密顿量，是一个具有形变的Nilsson势，Nilsson势参数为k和μ，其值取自文献[14]，是考虑了自旋轨道耦合的谐振子势，λ为化学势，N为粒子数，第三项是对力项，对效应的处理采用BCS理论[15]，第四项是科里奥利力.式(1)中的前三项组成原子核的核实部分的能量，第四项是对应组态的准粒子能量和.

系统的总能量是三个形变参数的函数，也是原子核的质子数和中子数的函数，在确定的质子和中子数下，对总能量的位能面求极小，则根据能量最低原理，相应的极小值应该对应原子核的稳定态，从而得出原子核的稳定形变值.

3 计算，讨论和结论

对Lu同位素的三轴计算中，由于它是奇质子数原子核，人们认为其组态至少是基于一个i13/2轨道质子的激发.对偶偶核174Hf，其最低激发态也应该是具有一对核子拆对的核子组态，鉴于实验中发现的几条超形变带，我们认为至少有两对核子拆对才能布居到那样的能级，因此本文中我们将选取四准粒子部分组态（表1），转动频率ω=0.02hω0，由于较低的转动频率，所以我们所选取距离费米面较近的组态.本文所做的是固定ε4=0.03的二维计算.

图1所示是各部分能量的位能面图.在上面的壳修正位能面图中我们可以看到，在质子壳修正图中具有很大四极形变和三轴形变区域出现局部极小值，然而在中子壳修正图中，对应区域却出现极大值，并且由于中子壳修正的影响更强（中子壳修正能量普遍都要比质子壳修正能量大），所以我们可以在总壳修正图中看到，在对应的区域出现的是与中子壳修正一致的局部极大值.不过，在这个区域的附近，还存在几个局部极小值，在Lu核的研究中我们知道，壳修正在总位能中起了很重要的作用，因此在这个Hf核的总位能面中还是具有出现局部极小值的可能性.

图1 各部分能量位能面

表1 单粒子组态

对总位能面有很大影响的还有准粒子能量.表1中所列出的是费米面附近的几个单准粒子组态，所有单粒子组态的能量都进行了计算.图2所示的是所选的三个准粒子组态的总位能面图和各自相对应的中子准粒子和质子准粒子位能面图.从中可以看到，在所选的三个准粒子组态的总位能面图中，都没有发现可以表征三轴超形变存在的局部极小值.然而,可以一致地发现，质子准粒子在三轴超形变区域都存在着极小值，因此，质子准粒子是有利于三轴超形变存在的.中子准粒子的能量分布比质子准粒子的能量分布要更复杂一点，不过，由于在三轴超形变区域并没有明显的极小点，所以它不会对壳修正能量起加强的作用.对其他组态形式也进行了计算，都与这五个组态所表现出来的性质是一致的.

图2 Total：总位能面图,nquasi：中子准粒子位能面图,pquasi：质子准粒子位能面图

在总位能面中，还包含对能、转动能和液滴能等其他部分的能量，可以看到，原本在壳修正和准粒子位能面中存在的局部极小值被平衡掉了，并没有得到可以表征三轴超形变存在的明显的第二极小值点.因此，在所选的转动频率和这几个组态下，并不具有三轴超形变的性质.提高转动频率和改变组态是使原子核出现三轴形变的有效方法.

在TRS中，不同组态的准粒子能量会对总能量有一定的影响，对组态的准确选取是很重要的.我们希望能够更有效地选取组态，究竟什么样的组态才是适合的呢？对于组态能量的分布特征，我们是希望它能有利于局部极小值的出现.如果假设核实的能量在三轴超形变区域的分布是均匀的，那么，我们就希望准粒子占据图3中实线1那样的轨道组态，本身的能量分布就具有极小值.通过这样的方法，我们先分析核实的能量分布特点，然后选取有利于在三轴超形变区域出现极小值的轨道组态，那么这样的组态就可能是TSD带所对应的粒子组态.但是，同时也要考虑组态的实际存在性，首先对应的轨道不能是费米面下面的轨道，其次还要符合跃迁定则等规律.这样的方法是否有效，还有待于通过进一步具体的计算来验证.

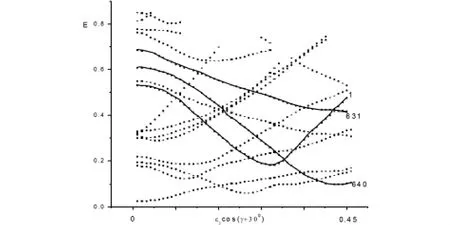
图3 单粒子轨道能量随ε2cos(γ+30°)的变化关系图

从图1中核实的位能面图我们可以看到能量分布的特点，依据上面的方法，我们就可以试图寻找相应的轨道曲线特点.巧合的是，我们所选的中子组态轨道[640]1/2和[631]3/2，不管旋称为正负，正好都具有相应的特点，而且对于质子，也具有这样的特点.然而，不幸的是，由于各部分能量综合作用的结果，并没有得到总位能面中的第二极小值.也许，在稍微远离费米面上面的具有更高能量的组态形成了实验上所发现的TSD带.