数学核心素养下小学数学“联·变”教学策略谈

蔡萍芬

（石狮市第三实验小学，福建 泉州 362700）

数学学科中充满丰富的联结与变式，它们是以知识的数学本质为基础展开的数学学习方式。教学中让学生寻找联结，建立数学知识体系，形成结构化思维；善用变式让学生实现知识的融会贯通，具有举一反三、触类旁通的灵动思维，应是小学数学教育追求的目标，以实现纵横通达、灵变活用的课堂教学景观。

一、借助直观模型，勾联生活与数学模型

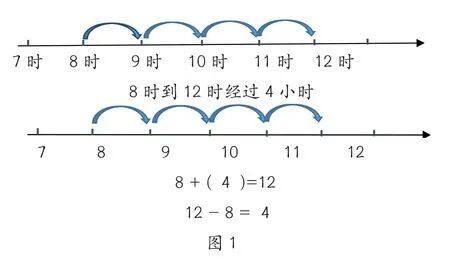
数学抽象性与学生认知特点直观性之间的矛盾是造成学生数学学习困难的重要原因之一［1］。教学中，我们常借助小棒、计数器、数线、点子图等直观模型帮助学生理解概念、法则、规律、性质等纯数学的抽象思考［2］。借助直观模型，还能有效建立生活原型与数学模型之间的联系，打通学生思维跨越的盲区，促进学生对数学本质的把握。如：执教二年级上册《一天的时间》，把钟面上的圆形间隔“化曲为直”成数轴，迅速激活学生原有的数数经验，学生在数轴上数出经过时间的过程与数轴上数出减法结果的模型是一样的（如下图1），稍加引导学生就能用减法来计算经过的时间，即“结束时刻-开始时刻=经过时间”。课尾，把生活中经历的不同时刻在数轴上标注，让学生直观感受到时间就是一把度量的尺，与长度测量的本质是一样的。

二、借助学具操作，盘活经验触类旁通

孩子的思维是从手指开始的，数学不能仅仅是脖子以上的思考。让学生借助学具的操作积累丰富的表象，能使学生的新知学习更快的找到思维链接点。借助学具演示操作，能突破语言表述的局限，打破“心求通而言不达”的尴尬境地，触发学生顿悟，盘活经验而触类旁通。

如教学四年级上册《观察物体》，教学难点之一是：两个不同平面上的面，从一个方向观察画出的三视图是在同一个平面上的情况（如下图2）。如何突破学生无法“眼见为实”的局限？借助学具让其穿板而过，观察留下的印记，就能达到预期的效果。这个过程的体验，让学生想象与实景相呼应，推理与实践相结合，较好积累学生的观察经验。

三、借助问题引领，推进探究积累经验

问题是引发学生思维的不竭动力，能围绕教学目标提出恰当的问题是一名教师的基本专业技能［3］。好的问题串，既是课堂教学的逻辑线索，也是促进数学学习“求联求变”的有效手段，更是达到积累数学活动经验的有力保障。如：六年级上册《反弹高度》，这是一节数学综合实践课。要求通过实验探究、数据分析得出影响球反弹高度的结论。重在让学生经历问题产生、提出、解决与应用的过程，提升学生实践研究的能力。基于此，把握住实验研究的难点与盲点，设计系列问题串，才能推动研究向科学化、有效化、数学化的方向前行。如：课始“影响球反弹高度的因素有哪些？”学生结合生活经验，大胆猜想确定研究方向；学生提出“篮球与乒乓球反弹高度是多少，哪种球高些”的研究问题，初步实验后，抛出问题串“刚才的实验存在什么问题？由一次实验观察到的结果就下结论，这样对吗？在实验的过程中，遇到哪些问题与困难？”这些基于实践生发出的问题，把学生研究引向深入，聚焦于研究的重点，进而达到科学、规范、严谨的实验探究。

四、借助类比推理，推动思考向纵深发展

推理是数学基本思想之一，在数学学习中随处可见，对促进学生的深度思考起着至关重要的作用。巧妙运用推理，激发学生类比思考，可探知数学本质，拓宽学生思维的深度与广度。如执教五年级上册《认识底和高》，在动笔画完平行四边形、梯形、三角形的高后，让学生观察三种图形作高的共同点与不同点（如图3），学生在类比的思考中，发现高都是在一组平行线间或点与线间所做的垂线段，揭示高的本质。不同是由于图形本身所具有的特征，高的条数不同：三角形只有三条高，平行四边形可以在两组平行线间做无数条高，梯形只能在一组平行线间做无数条高。经历这样直观推理的过程，类比推理的体验是充分的，也就能自发类推到更多作图题解中。

五、借助思维导图，融通知识建构体系

学科思维导图是一种基于系统思考的知识建构策略。融合可视化、结构化、逻辑化、辩证思考、追问意识等思维方式，是一种有效的思维模式［1］。小学数学分为数与代数、图形与几何、统计与概率、综合与实践，其中数与代数、图形与几何两个领域特别适合用思维导图进行体系的梳理，可以是树状图、并列图、表格等多样的形式。

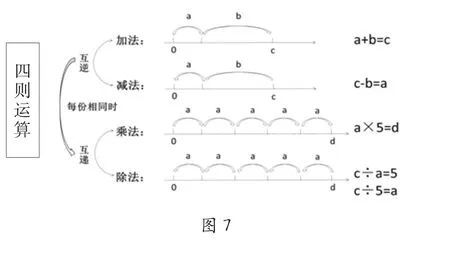
数与代数领域包括：数的认识、加减乘除、混合运算的认识、实际问题的解决及方程等多个知识板块。学生要接受的知识点多而散、学习时间跨度长，容易造成知识与技能的机械操练与块状记忆，无法达到融会贯通。如何实现知识间的联结思考？应该回到这部分知识的本源，那就是数（shu），而数源于数（shu）。数与代数领域许多知识的基础就是数数，如：加法运算是1个1个顺着数；减法是1个1个逆着数；乘法是跳着数，每次跳着数的距离是一样的；除法则是乘法的逆数。根据这样的认知，我们可以用数轴的形式对四则运算意义进行梳理（如下图7），借助直观图示，学生豁然感悟到：运算的本质就是分与合的过程。