单机上简单线性退化工件的随机在线调度问题
2018-10-17刘辉冉
刘辉冉,马 冉
(河南理工大学 数学与信息科学学院,河南 焦作 454000)
0 引言
在经典的调度问题中,工件的加工时间通常是一个确定的常数.但是,在实际问题中,工件的加工时间可能是一个随机变量,所以有必要考虑带有随机信息的排序问题.带有随机信息的调度问题由DANTZIG[1]和BEALE[2]首先提出,他们假设所给实例中的某些数据并不是预先给定的确定常数,而是服从某种概率分布的随机变量.
本文重点考虑工件的加工时间是随机变量的排序问题,即工件加工时间的期望是关于工件的开工时刻和退化率的简单线性函数,我们通常把这类问题称为简单线性退化工件的随机调度问题.
GUPTA[3]首先提出了具有退化效应工件的调度问题.MOSHEIOV[4]讨论了工件的加工时间是开工时刻的简单线性增加函数的单机排序问题,其目标函数是最小化完工时间和,并给出了最好可能的SDR算法.注意到SDR算法也是一个在线列表算法,但是此算法对在线问题来说不是一个最好可能的算法.VESTJENS[5]证明了平行机上的确定性在线问题不存在竞争比小于1.309的算法,并证明了可中断情形下的在线问题不存在竞争比小于22/21的算法.CHENG等[6]证明了机器可拒绝具有退化效应工件的排序问题是NP-hard的.NG等[7]证明了简单线性退化工件在单机上进行可中断排序且目标是最小化工件加权总完工时间和的在线调度问题是NP-hard的.因此,这类问题的不可中断情形亦是NP-hard的.而LIU等[8] 对可退化工件的确定性在线排序问题1|online,rj≥t0,pj=bjSj|∑Cj给出了竞争比为1+bmax的最好可能的在线D-SGR算法.在2015年,刘其佳和冯琪[9]研究了单机上考虑运输的退化工件的在线排序问题,即1→D|online,rj≥t0,pj=ajt,v=1,c=|Dmax,其中表示工件的最大运输完工时间,给出了最好可能的竞争比为1+α的在线算法D.MA等[10]研究了问题1|online,rj≥t0,pj=αj(A+BSj)|∑wjCj,对LIU等在文献[8]中探究的问题进行了推广,并且给出了竞争比为1+λ(A)+αmaxB的最好可能的DSWGR算法.CHEKURI等[11]对同型机上的在线调度问题进行了研究,即并给出了竞争比为3-1/m的在线算法.WAGNER等[12]利用线性规划方法给出了竞争比为2.618的算法,MEGOW等[13]对其可中断情形给出了竞争比为2的在线算法.MA和YUAN[14]对单机上具有拒绝权利的在线调度问题给出了竞争比为2的最好可能的在线算法.随后,他们[15]将此类问题推广到了平行机上,并对同型机和同类机上的情形分别给出了竞争比至多是4+ε和8的在线算法.
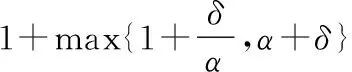
的1-SEPT算法.顾满占和鲁习文[19]讨论了同类机上的随机在线排模型,给出了竞争比为
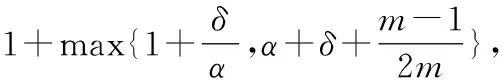
然而,关于简单线性退化工件的随机在线调度问题,目前几乎没有任何研究进展.本文对简单线性退化工件在单机上的随机在线调度问题进行了研究,并对该问题给出了一个竞争比为1+bmax的SHIFT-SDR算法.LIU等[8]所研究的问题是我们所研究问题的一个特例,因此本文给出的SHIFT-SDR算法是最好可能的在线算法.
1 问题描述
设有一个工件集J={J1,J2,…,Jn},其中的n个工件均以时间在线的方式到达,只有工件Jj到达之后,决策者才知道工件的释放时刻rj≥t0(t0>0),退化率bj(bj>0)及加工时间的期望E[Pj],且工件加工时间的期望依赖于工件的开工时间,即E[Pj]=bjSj.由于工件加工时间的期望与其开工时间有关,因此直到工件完工之后排序者才知道随机变量Pj的一个实现值.目标是最小化工件总完工时间的期望,三参数法表示为1|online,rj≥t0,E[Pj]=bjSj|E[∑Cj].
引理1[8]对于问题1|online,rj≥t0,Pj=bjSj|∑Cj,任意确定性在线算法的下界不会好于1+bmax.
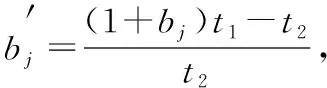
2 算法及其分析
2.1 SHIFT-SDR算法
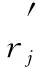
步骤2:根据修正后的释放时刻,在任意时刻,如果机器是空闲的,从所有的就绪工件中选择退化率最小的工件进行加工;
步骤3:如果没有新工件到达,则算法终止;否则,返回步骤1.
2.2 竞争比分析
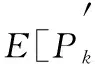
给定实例I,I中的工件集为J={J1,J2,…,Jn},运用SHIFT-SDR算法对实例中的工件进行排序加工,并把得到的排序记为σ.
引理3σ序中仅包含一个单块,即在第一个加工工件的开工时刻之后,所有的工件进行连续地无中断加工.
证明(最小反例法)假设σ序中包含两个子块σ1和σ2,显然σ1和σ2是互不影响的.此时可将实例I划分为两个相互独立的更小的实例I1和I2,即I=I1+I2.假定实例I、I1和I2的最优排序分别为π、π1和π2,那么I1和I2中的工件在π中的排序是一个可行排序.记σ、σ1、σ2、π、π1和π2所对应的目标函数值分别为:C(σ)、C(σ1)、C(σ2)、C*(π)、C*(π1)和C*(π2).通过上述分析,可以得到:
C*(π1)+C*(π2)≤C*(π),
由引理1的结论,可以得到
又因为

由引理3的结论,我们可以根据σ序中工件的退化率对σ进行分块处理(每个子块之间没有空闲时间).
假定σ序可分成k(k≥1)个子块B1,B2,…,Bk,子块具有以下几个性质:
性质1 每个子块中工件以SDR规则排序,即在每个子块中,工件根据退化率进行从小到大的排序;
性质2 相邻的两个子块Bi和Bi+1,1≤i 性质3 令b(i)=min{j>b(i-1)|bj>bj+1},b0=0,则 Bi={Jb(i-1)+1,Jb(i-1)+2,…,Jb(i)}; 引理4 令E[C*(I)]和E[C*(I(σ))]分别是I和I(σ)在无中断最优排序下的总完工时间的期望,则 E[C*(I(σ))]≤(1+bmax)E[C*(I)]. 因此 E[C*(I(σ))]≤(1+bm(i))E[C*(I)]≤ (1+bmax)E[C*(I)]. 证毕. 对于实例I,如果中断被允许,由引理2可知,SRDR是I的最优中断排序.下面就利用此最优中断排序来证明SHIFT-SDR算法的竞争比是1+bmax. 引理5 实例I在SHIFT-SDR算法下得到的排序σ,是实例I(σ)在SRDR算法下的一个排序. 那么 综合上述两种情形可知,任意两个连续子块之间也满足SRDR规则.因此σ是I(σ)在SRDR算法下的一个排序.证毕. 通过引理5得出: E[CSHIFT-SDR(I)]=E[CSRDR(I(σ))]≤ E[C*(I(σ))]≤E[C*(I)]. 因此定理1成立: 定理1 对随机在线调度问题1|online,rj≥t0,E[Pj]=bjSj|E[∑Cj],SHIFT-SDR算法是最好可能的在线算法,其竞争比为1+bmax. 本文通过改变就绪工件的释放时间,对简单线性退化工件在单机上的随机在线排序问题设计了一个竞争比为1+bmax的在线算法.这与其在线排序问题的下界相匹配,因此,本文所研究的问题给工件的加工时间服从某个具有概率分布的简单线性退化工件的随机在线排序问题提供了一个下界.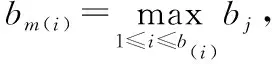
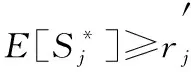
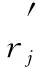

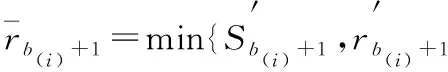
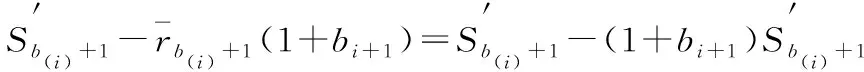
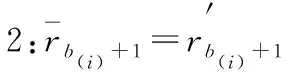
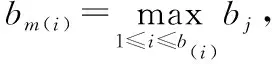

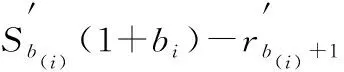
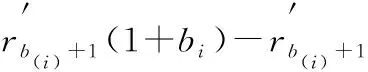

3 结语
