一族离散的刘维尔可积系及其耦合系统

李 柱

(信阳师范学院 数学与统计学院, 河南 信阳 464000)

0 引言

寻找新的可积系统及其哈密顿结构是孤立子理论研究中的一个重要的课题.1990年屠规彰教授提出了构造离散哈密顿系统的简洁方法[1],利用此方法得到了许多离散的可积系统[2,3].文献[4]讨论了构造孤子解的方法.近年来,构造可积系统的耦合系统是一个热门课题,马文秀等提出了一个行之有效的方法[5],具体思路如下：

设G是一个李代数,作G与李代数Gc的半直和

(1)

做扩展的等谱问题：

(2)

由其相容性条件可得扩展的零曲率方程：

(3)

即

(4)

由式(4)可得耦合系统：

(5)

文献[6]讨论了此方法在离散可积系统里的应用;文献[7]讨论了此方法在高维李代数情况下的应用;文献[8]讨论了此方法在(2+1)-维情况下的应用.本文将利用屠格式的方法得到一族刘维尔可积系, 并借助李代数的半直和方法构造其可积耦合系统.

1 离散的可积系统

文献[1]中给出了如下的李代数：

G=span{e1,e2,e3,e4},

(6)

其中：

容易验证在如下的矩阵乘法下G是封闭的.

(7)

设ei(n)=eiλn,i=1,2,3,4,则

(8)

令

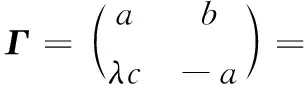
bme3(-m)+cme4(1-m)).

(9)

解静态零曲率方程：

(EΓ)Un-UnΓ=0,

(10)

得递推关系

(11)

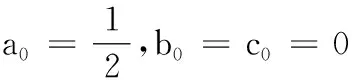
aj[u]=0=0,bj[u]=0=0,cj[u]=0=0(j≥1),

其中[u]=(u,Eu,E-1u,…)，则递推关系(11)可以唯一地确定aj,bj,cj,j≥1，并且依次可求出

对任意的m≥0,取

bme3(n-m)+cme4(n+1-m)，

(12)

则直接计算得

(EΓ+)Un-UnΓ+=

(13)

故由离散的零曲率方程可得如下的Lax可积系：

(14)

由递推关系(11)可得递推算子L满足

(15)

其中：

则系统(14)可写为

(16)

当n=0时,系统(16)约化为如下的平凡方程：

(17)

当n=1时,系统(16)约化为如下的非平凡方程：

(18)

2 系统(16)的哈密顿结构

定义

c+qc+pae4,

(19)

〈A,B〉=Tr(AB),其中A,B是同阶方阵.容易计算，

Tr(e1e1)=Tr(e1e1)=Tr(e3e4)=

Tr(e2e2)=Tr(e4e3)=1,

其余的为0,

因此可得,

由迹恒等式

(20)

可得

(21)

比较λ-n-2的系数得

(22)

令n=0,则ε=0.因此,有

(23)

故系统(16)具有如下的双哈密顿结构：

(24)

其中K为

K=JL=

(25)

容易验证J*=-J,K*=-K,即J,K是反对称的.下面证明K满足Jacobi恒等式

〈K′(u)[Kf]g,h〉+〈K′(u)[Kg]h,f〉+

〈K′(u)[Kh]f,g〉=0,

(26)

其中

f=(f1,f2)T,g=(g1,g2)T,h=(h1,h2)T,

(27)

为三个任意的向量函数,u=(p,q)T.

事实上,由式(25)直接计算得

(28)

(29)

其中

K11=F1(E+1)(E-1)-1p+

p(E+1)(E-1)-1F1,

K12=-F1(1+q)-pF2,

K21=F1(1+q)+pF2.

由此可得

〈K′(u)[Kf]g,h〉=

F1(E+1)(E-1)-1pg1h1+

p(E+1)(E-1)-1F1g1h1-

F1(1+q)g2h1-pF2g2h1+

F1(1+q)g1h2+pF2g1h2=

p(E+1)(E-1)-1pf1(E+1)(E-1)-1pg1h1+

p(1+q)2f2g2h1-p(1+q)2f2g1h2+

p(E+1)(E-1)-1p(E+1)(E-1)-1pf1g1h1+

p2(1+q)f1g1h2-p2(1+q)f1g2h1-

p(1+q)f2(E+1)(E-1)-1pg1h1-

p(E+1)(E-1)-1p(1+q)f1g2h1+

p(E+1)(E-1)-1p(1+q)f1g1h2-

p(E+1)(E-1)-1p(1+q)f2g1h1.

(30)

类似地可求得〈K′(u)[Kg]h,f〉和〈K′(u)[Kf]g,h〉.通过复杂的计算可得

〈K′(u)[Kf]g,h〉+〈K′(u)[Kg]h,f〉+

〈K′(u)[Kh]f,g〉=0.

(31)

同理可证,J也满足Jacobi恒等式

〈J′(u)[Jf]g,h〉+〈J′(u)[Jg]h,f〉+

〈J′(u)[Jh]f,g〉=0.

(32)

因此J,K是哈密顿算子.递推算子L的共轭算子为

(33)

其中

则

L*J=

(34)

下面考虑Poisson括号

(35)

于是,

(36)

同理可得

(37)

因此

(38)

并且

(39)

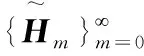
3 系统(14)的可积耦合

令

G1=span{f1,f2,f3,f4,f5,f6,f7,f8},

(40)

其中

(41)

容易验证G1在如下的矩阵乘法下是封闭的.

(42)

记G2=span{f1,f2,f3,f4},G3=span{f5,f6,f7,f8},则G2,G3同构于G,且

G1=G2⊕G3,

[G2,G3]⊆G3,G2是G1的理想.设

fi(n)=fiλn,i=1,2,…,8,

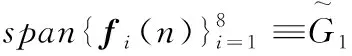
(43)

令

bmf3(-m)+cmf4(1-m)+

dmf5(-m)-dmf6(-m)+

gmf7(-m)+hmf8(1-m)).

(44)

解零曲率方程：

(EΓ)Un-UnΓ=0,

(45)

得下面的递推关系：

(46)

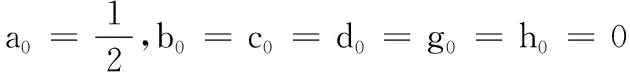
aj[u]=0=0,bj[u]=0=0,

cj[u]=0=0,dj[u]=0=0,

gj[u]=0=0,hj[u]=0=0,(j≥1),

其中[u]=(u,Eu,E-1u,…),则递推关系(46)可以唯一地确定aj、bj、cj、dj、gj、hj,j≥1,并且依次可求出

对于任意的整数m≥0,取

bmf3(n-m)+cmf4(n+1-m)+

dmf5(n-m)-dmf6(n-m)+

gmf7(n-m)+hmf8(n+1-m)).

(47)

直接计算得

(EΓ+)Un-UnΓ+=

(bn+1+gn+1)e7(0)+

(48)

则由离散的零曲率方程得如下方程族：

当r=s=0时,系统(49)约化为系统(14).因此,由可积耦合的定义可知，系统(49)是系统(14)的可积耦合.

4 结束语

本文得到了一族具有双哈密顿结构的刘维尔可积系,并构造了其耦合系统,利用同样的方法也可以进一步构造其双可积耦合系统.今后我们将进一步讨论其达布变换、守恒律、对称结构和代数几何解等可积性质;如何把构造耦合系统的方法推广到超可积系统也是值得我们今后研究的重要问题.