PISA数学素养之精熟度水平及典型试题分析——PISA数学素养测试研究之二

金 彩，邵光华

（浙江省宁波华茂国际学校；宁波大学教师教育学院）

PISA数学素养测试是针对处于基础教育即将结束阶段的15岁左右学生数学素养的一种评估，考查该年龄段学生在面对大部分真实情境问题时熟练运用数学的程度.根据测评框架，项目组结合测试题目的难度与要求设计了评估学生数学能力的精熟度水平.在文［1］中，笔者对PISA数学素养如何界定及数学过程与能力的运用做了详细的分析，本文将进一步分析PISA测试中数学精熟度水平及试题，寻求改善我国基础数学教育发展的启示及建议.

一、PISA测试中数学精熟度水平

PISA数学素养的评估采用精熟度水平等级来描述学生的相应能力.精熟度水平等级与题目难度相关联，即水平等级越高，与之相应的题目越难.数学素养的精熟度水平是由专家组确定相应的共同特征和要求，并对相应的题目难度进行区分，各项题目预设的难度还要依据参与国家或地区学生的成绩来校验.题目的难度范围反映了一系列有序知识、技能及策略构建的数学素养.这样，PISA评分者将学生在数学试题上所获得的成绩，转化为精熟度水平量表上的素养得分，学生成功解决与某精熟度水平相应难度的大部分题目，就可视学生处于该精熟度水平的上端；若成功解决至少一半的题目，则处于该精熟度水平下端.也就是说，在同一精熟度水平内，分数越高，学生成功解决相应水平题目的比例越高.数学精熟度水平被分成6个水平等级，每个等级代表着不同难度的题目群，等级6为最高水平，等级1为最低水平.PISA 2003与PISA 2012均是以此为基础对学生的数学素养进行描述，如表1所示.

表1：PISA精熟度水平等级概述及等级的临界分数

表1中低于1级水平的学生并不表示他们不具备任何数学能力，只是尽管问题情境是学生熟悉的，问题解决策略可以直接观察得到，但他们也不能使用合适的数学技能去解决问题.

每一等级水平的临界分数由计算出来的题目难度决定，是运用统计学设定量表上的临界分数，使每个相邻的等级之间的题目难度变化大致相等.不同等级所划分的临界分数所代表的意义有以下两点：第一，比较不同水平学生的成绩分布；第二，区分不同水平的题目特征和学生的表现特点.PISA 2012数学精熟度分量表是基于3个数学过程来划分的，PISA 2003是依据4个数学内容来划分的，这是专家在发展和完善数学素养测评框架时，考虑到数学过程对考查学生的实际能力，以及对反馈和指导教学实践更有意义所做出的改进.

二、PISA典型数学试题分析

基于文［1］及以上对PISA 2003和PISA 2012数学素养的分析，针对PISA数学素养测评框架的运用，下面选取PISA 2012测试中的典型数学试题做具体分析.

题目1（爬富士山）富士山是日本一座著名的休眠火山.御殿场（日本著名百货公司）至富士山顶大约有9 km，步行者需要在晚上八点前返回御殿场，来回共18 km.Toshi（人名）估计他上山的平均速度为1.5 km/h，下山则是上山时两倍的速度，这个速度包括午饭和休息所花时间在内.如果Toshi使用估计的速度上下山，要在晚上8点前返回到出发地，那么他最晚必须几点钟出发？

该主题考查的核心概念是速度，因而属于变化和关系类别，此情境属于社会性情境.问题的重点涉及创建一个可以回答该问题的数学模型，属于数学化的表述情境.问题解决者需要理清题目中所给数据之间的关系，对学生数学化，运用符号化的、正式的、技术性的语言和运算，推理与论证的能力要求较高.

题目2（旋转门）三翼式旋转门在圆形的空间内旋转，圆形空间的直径是200 cm，旋转门的三片旋转翼把空间等分成三个部分.如图1所示的俯视图显示了旋转翼三个不同的位置.

图1

问题1：两片门翼所形成的角的度数是多少？

问题2：旋转门的出、入口（图2中的弧形虚线）大小相同.如果出、入口太宽，正在旋转的旋转翼则无法形成密闭的空间，空气便能在出、入口之间自由流动，造成不必要的热量增减.要使空气无法在出、入口自由流动，每个门口的最大弧长是多少？

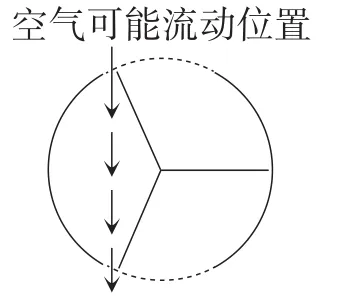
图2

该主题的数学内容是空间和图形，数学情境属于科学性情境.问题1属于运用数学概念、事实、步骤和推理过程类别，侧重于利用相关的数学概念进行运算，对陈述的数学能力有较高要求；问题2是数学化的表述情境，重点是创建回答所提问题的数学模型，对学生数学化、推理和论证的数学能力要求较高，解决此问题在于对圆的相关概念知识的掌握及从自然语言中抽离出数学关系.很多事物存在于生活中是有其原理及规律的，数学是描述这些原理和规律的根本，数学学习是学会用数学的眼光去看待生活、解决问题.

题目3（购车）Chris（人名）刚考取了驾照，她计划购买一辆二手车.表2显示了她所了解的四辆汽车的详细信息.

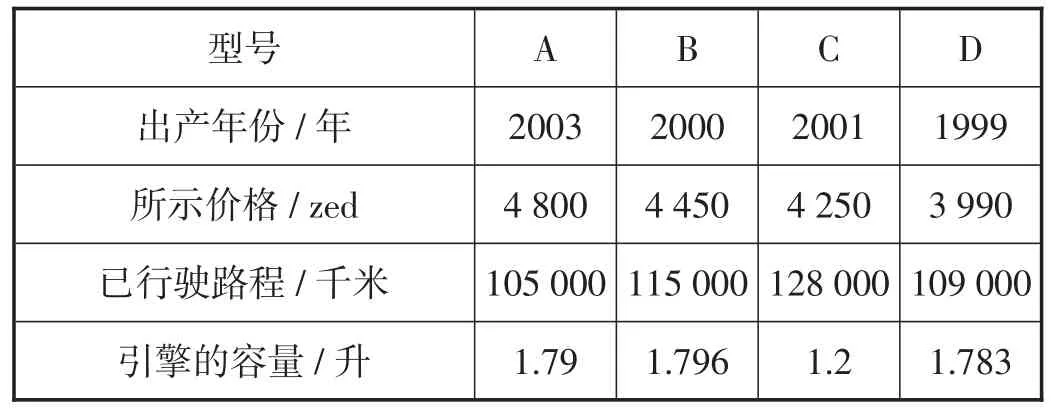
表2

若Chris需要额外缴付汽车价格的2.5%作为汽车的税款，那么她购买A汽车需要缴纳的税费为多少？

该主题属于个人性情境类别，数学内容属于数量类别，难度适中，涉及计算问题，解题过程需要运用数学概念、事实、步骤和推理.此题需要用到百分数的计算，故涉及沟通、数学化、陈述及运用符号化的、正式的、技术性的语言和运算的数学能力.这个主题测试是人们生活中的交易问题，与真实生活很贴近，学生能真切体会到数学就在我们的身边.

题目4（图表）1月，乐队4U2Rock和The Kicking Kangaroos都发布了新专辑.2月，乐队No One’s Darling和The Metalfolkies也发布了新专辑.图3展现了这些乐队1月至6月的专辑销量情况.

图3

问题1：在哪个月，乐队No One’s Darling第一次比乐队The Kicking Kangaroos卖出的专辑多？

（A）不是1月 （B）3月 （C）4月 （D）5月

问题2：乐队The Kicking Kangaroos的经理非常焦虑，因为乐队专辑的销量从2月到6月一直下降，如果相同的消极趋势持续下去，该乐队7月份的专辑销量估计会是多少？

（A）70张 （B）370张

（C）670张 （D）1340张

该主题测试的问题情境和内容分别是社会性情境、不确定性和数据.在数学过程类别来看，问题1是对图表中呈现的数学信息做解释，归属于阐释、应用和评估数学结果过程类别；而问题2侧重于运用程序性知识进行数学陈述，以做出进一步的推论，是运用数学概念、事实、步骤和推理类别.两个问题的难度较低，对推理、论证和设计策略的能力要求较高.现如今是经济发展的高速时期，各种报表在报纸、杂志、网络等媒体中都能随处可见，从表格中的数据获得有用信息，这是现今公民重要的素质之一.

以上4个主题、6个问题题目难度，以及在3个维度上的分布关系如表3所示.

表3：PISA2012试题的三个维度分布

由以上分析可见，PISA 2012基于以数学表述、数学运用和数学阐释的3个数学过程来考查学生的数学素养.各试题归属于相应的数学过程类别，且在完成某一数学过程对所运用的数学能力的要求是不一样的，不同的数学过程中运用相同的数学能力在程度上也有所差别.在不同精熟度水平下，明确给出了不同学生能达到不同的数学能力的程度.如此，评分者就能更注重学生在解答过程中数学过程的展现及数学思想方法与能力的应用，而不以单纯的结果评估问题的解答来判定学生的数学能力水平.同时，还能更客观判断学生数学能力发展所存在的问题，有助于进一步改善教育教学的方式.

三、启示

通过上述分析可见，PISA数学素养测试明确界定数学问题解决的过程，以及数学能力来考查学生的以数学思维能力为核心的数学素养，即可归结为“数学知识（技能）—数学应用—数学推理”3个要素，并以这3个要素为基础形成数学知识呈现的基本过程，着重考查学生的数学探索和思考能力，突出数学思维的核心作用.我们可以从中获得一些对完善正处于改革阶段的基础数学教育的启示及建议.

1.注重学生思维过程的暴露和引导

数学教育是一门培养学生的思维能力的学科，而数学课堂教学是培养数学思维能力的主要场所，数学课堂教学评价对学生的思维能力的形成起到重要的作用.通过对PISA数学测试的研究，我们认为数学课堂教学更应该注重学生思维过程的暴露和引导.在以往的数学课堂中，教师往往是抛出一个问题，让学生思考后给出问题的答案，关注的重点在于问题是否得到了解决，而不在于问题是如何得到解决的，也就是很少关注学生的思维过程.在课堂上评价学生思维的生成，所提出的问题要有一定的层次性，在学生给出答案的同时，并告知自己是如何思考的.这样，我们就能更确切地了解到学生是如何解决问题的，获得其解决问题的思维过程，进而帮助学生在思考中获得提高.在课堂上，通过巧设问题，不仅要关注学生的答案，更要关注学生的思维过程.

2.注重思维发展的过程性评价

通过研究PISA数学测试对学生数学素养的评估，我们了解到，学生数学能力的发展，不仅仅包括知识和技能的增长，还包括学生认知水平的提高与发展，以及将数学学科知识应用于现实生活中的能力.而在当下的学习评价机制中，我们往往关注问题解决的结果，而常常忽略问题解决的方法和过程.仅仅一个问题的结果不能说明学生的能力强弱，要全面考查学生的数学能力，必定要重视学生解决问题的思维过程（包括假设的形成、证据的运用、结果的判断等），关注学生认知水平的提高与发展，同时要采用过程性评价.过程性评价能帮助我们了解学生在能力发展中的收获、困惑和问题，还能适时有效地指导学生进行自我反思，获得持续进步和良性发展.

总而言之，在数学教育教学的过程中，对学生数学能力的培养，要将数学思维的发展作为核心，推动学生在掌握知识和技能的基础上发展认知能力.在运用数学知识解决问题的过程中，培养学生的数学应用意识和思考的能力，促使学生形成用数学的眼光观察、分析并解决生活中遇到的实际问题.