指向高阶思维的数学课堂教学策略——基于“直角三角形全等的判定”的教学实践

冯 剑，周庆忠

（浙江省杭州第十中学；浙江省杭州市富阳区教育发展研究中心）

强化并贯穿于各种教育目的的中心目的——教育的基本思路，就是要培养思维能力.美国教育家布卢姆按照认知的复杂程度，将思维过程具体化为六个类目的行为表现，由低到高包括记忆、理解、应用、分析、评价、创造.其中，前三者是低阶思维，体现在学习事实性知识或完成简单任务的能力，是较低层次的认知水平；而分析、评价和创造为高阶思维，是发生在较高认知水平层次上的心智活动或认知能力.《义务教育数学课程标准（2011年版）》倡导的是问题解决、自主学习、合作学习、探究学习的学习方式，进而培养学生问题解决能力和创新能力，这种教学方式的变革需要我们的课堂从低阶思维走向高阶思维.学生数学核心素养发展需要培养学生的理性精神、数学思考、思维能力，这些核心素养的关键因素需要我们的课堂从低阶思维走向高阶思维.信息时代，需要的是如何学会检索、操纵信息，学会筛选、重组和应用信息，这些计算机所不能的思维也需要我们的课堂从低阶思维走向高阶思维.从教学方式的变革、素质教育目标的达成、信息技术的发展来看，高阶思维已成为现代教学的核心价值取向和课堂教学的目标追求，同时也是提高教育、教学质量和培养创新人才的有效途径.那么，如何使数学课堂教学指向高阶思维呢？下面笔者以浙教版《义务教育教科书·数学》八年级上册第2章第8节“直角三角形全等的判定”为例，谈谈指向高阶思维的数学课堂教学的几点策略.

一、情境创设，在激发与同理过程中指向高阶思维

思维的行为表现要求学生把信息分解成一个个部分来加以理解，在课堂上伴随着学生的讨论、发现、深入思考、积极参与等行为.真实的、有意义的问题情境的创设，往往能激发学生的内隐学习动力，使学生参与课堂的讨论、思考，继而发现解决问题的方法.这样的情境导入有助于学生深化对所学知识的理解，有助于学生进行高阶思维活动，实现新的知识建构.

环节1：情境导入环节设计.

师：老师家里有一块如图1所示的直角三角形玻璃不小心弄破了，想到店里重新配一块.但是，老师到了商店却忘带了玻璃，那么老师需要知道哪些量，才能配到一块一模一样的玻璃呢？

生1：知道AB和BC的长度即可.因为，通过SAS可以证明直角三角形全等.

图1

生2：只要知道∠A的度数和AB的长度，用到证明直角三角形的方法是ASA.

师：很好！用证明三角形全等的方法可以确定直角三角形玻璃的大小和形状是一样的.那么，还有其他的方法吗？

生3：也可以用AAS，SSS来证明！

师：刚才大家用到已学的四种方法，证明了直角三角形全等的条件.请问老师只知道AB和AC的长度，可以配到一块全等的玻璃吗？

学生不由自主地相互辩论起来，有的说这是SSA，不能证明全等；有的说可以……

上述课堂导入环节，让学生自主探索证明直角三角形的条件，既复习了SSS，SAS，ASA，AAS等已学判定方法，又为HL定理的引出做好了铺垫.高阶思维的发生源自学生对意义的追求，所以课堂的情境导入是否能满足学生的思维需求就显得十分重要了.为了使课堂指向高阶思维，教师在此环节中可以跟进以下两种策略.

第一，设计有意义的情境.案例中需要知道哪些量才能配到一块一模一样的玻璃这一情境可以激发学生的学习兴趣，益于调动其已有知识和经验，并为问题解决提供持久的内驱力.课堂只有将问题解决所需要的学科知识、策略性知识及元学习知识镶嵌于真实、复杂的情境之中，激发学生主动学习的意愿，才能为高阶思维教学做好情感铺垫.

第二，设计具身性的问题.课堂的导入问题设计要充分考虑和尊重学生的差异，使学生能积极参与到课堂的讨论中来.案例中四种不同的证明全等的方法，以及对SSA能否证明直角三角形全等的不同想法的表达，都是学生不同认知习惯和认知方式的一种理解.这样的课堂才能实现思维的升格和新知识的意义增值.

二、定理探究，在探索与综合过程中指向高阶思维

思维的行为表现需要学生在深入思考、比较、评估的基础上做出决策，在课堂上伴随着学生的争论、比较、评价、决定、选择、证明、积极参与等行为.课堂的探究活动过程往往要求学生认真收集和处理问题的信息，经过观察、分析、综合、比较、选择、概括、猜想和证明等深层次的探索活动，并认真研究，才能获得解决问题的答案.指向高阶思维的课堂就需要这样的探索和综合活动过程.

环节2：探索定理环节设计.

问题：如图2，在△ABC和△A′B′C′中，∠C=∠C′=90°，AB=A′B′，AC=A′C′，求证：Rt△ABC≌ Rt△A′B′C′.

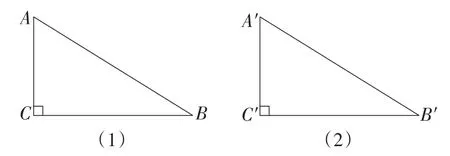
图2

师：小组讨论，合作探究.要求运用多种方法证明两个直角三角形全等.（可借用桌面上的两个直角三角形纸板进行探究.）

生4：在直角三角形中，我们可以利用勾股定理求得BC=B′C′，然后利用SSS证明这两个直角三角形全等.

师：很好！通过勾股定理计算可知第三组对应边相等.还有其他方法吗？

生5：如图3，我们把两个直角三角形拼成等腰三角形ABB′，根据等腰三角形的“三线合一”定理可知，AC是∠ABB′的平分线，然后利用AAS或ASA证明全等.

师：太棒了！利用直角三角形纸板，根据已知可拼成一个等腰三角形.这种方法叫做“构造法”！还有不同的想法吗？

生6：也可以拼成如图4所示的图形，连接CC′.

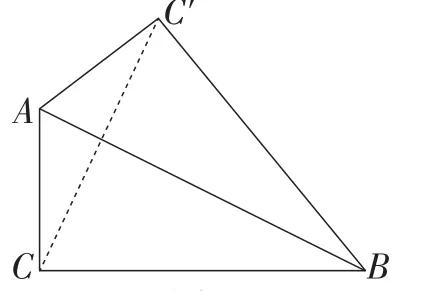
图4

由题意可知，△ACC′是等腰三角形，所以∠ACC′=∠AC′C.因为∠C=∠C′=90°， 所 以∠BCC′=∠BC′C.由此可得等腰三角形BCC′，从而得到BC=BC′，最后利用SAS证明全等.

师：真会动脑筋，图形构造得很好！下面大家用自己的语言来叙述一下这个直角三角形的判定定理.

学生归纳、交流、补充，教师对学生不严谨的语言进行改进.

文字语言：斜边和一条直角边对应相等的两个直角三角形全等.简写：“斜边、直角边”或“HL”.

几何语言：在Rt△ABC和Rt△A′B′C′中，可以由

案例中，整个定理探究活动由学生小组合作探究完成.用勾股定理证明比较容易想到，但构造法学生接触不多，较难形成思路.在探究时，鼓励学生用好两个直角三角形的素材进行拼接，使构造法更容易得到.高阶思维的形成需要富有探索性和创造性的探究活动，需要复杂多元和灵活多变的探究问题.为了使课堂指向高阶思维，教师在此环节中可以跟进以下两种策略.

第一，设计探究性活动.直角三角形判定定理的探索是本节课的重点和难点，如果只用勾股定理的方法进行证明，那么学生就失去了定理证明的探究过程.案例中，巧妙的利用两个直角三角形纸板让学生进行探索，使学生体验探索的过程，促进了学生学习方法的转变.两种利用构造法的证明方法，正是学生的创新精神和实践能力的有效体现.而这也是高阶思维课堂所要关注的重要要素.

第二，引导学生术语表达.众所周知，语言表达是概念学习过程中非常重要的一个环节.数学中各种结论的获得都要依靠逻辑推理，而数学语言表达能力直接影响逻辑推理的进行.案例中，由于前面已经有了充分的探索和讨论，故可试着让学生自己概括出定理的文字语言，教师在此基础上进行修正、提升，同时还需要从精密性的角度让学生解释定理的符号语言表达内容与之前所学的四个判定全等的定理的区别.

三、疑点突破，在批判与思辩过程中指向高阶思维

思维的行为表现需要学生在对问题分析、检查、探测、判断、评论、反思的基础上促进对知识的深层次理解.课堂教学疑点的突破需要学生严格的估计思维材料、评价解题思路选择的是否正确，以及评价这种思路必然导致的结果，精细地检查归纳、分析和直觉的推理过程.思维一定是由难题和疑问或一些困惑、混淆、怀疑引发的，指向高阶思维的课堂就需要这样的批判与思辨活动过程.

环节3：疑点突破环节设计.

生7：老师，直角三角形全等可以用HL定理，那么之前我们为什么说SSA不能证明三角形全等呢？

师：非常好，那么，我们就来探讨一下，在什么条件下，SSA能判定三角形全等.

生8：在直角三角形中，就是今天学习的HL定理！

师：很好！是不是只有在证明直角三角形全等时可以呢？究竟是什么原因造成的呢？下面大家先进行画图操作：如图5，已知线段c及∠θ（∠θ为锐角），画△ABC，使AB=c，∠A=θ，BC=a，并回答问题：其中，线段a的长度取何值时，能且只能画出一个△ABC？

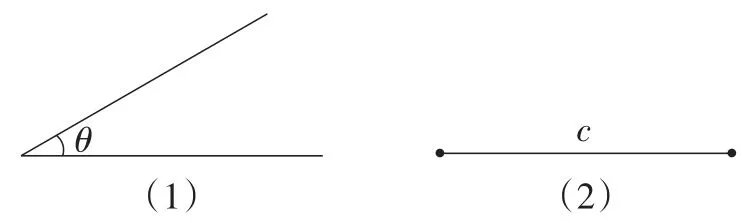
图5

图6

学生专注的思考、画图，教师巡视、指点.

生9：如图6，我发现△BCC′是等腰三角形，所以我画了两个△ABC.

师：没有关系，虽然没有完成任务，但是生9给我们提供了一个方向.那么，点C′一定能保证 画出这个等腰三角形吗？

生10：如图7，我发现当点C，C′重合，即当∠C=90°时，就只能画出一个△ABC.

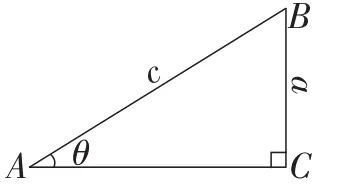
图7

师：为什么？

生10：因为在同一平面内，过直线外一点有且只有一条直线与已知直线垂直，所以当a等于点B到AC的距离时，能且只能画出一个△ABC.

师：很好！生10考虑了点C在直线AC上的特殊位置.还有其他情形吗？

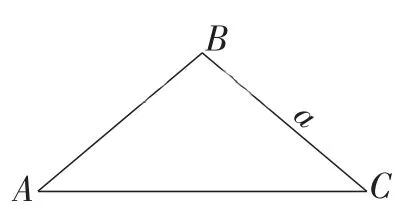
图8

生11：如图8，当a=c时，也只能画出一个△ABC，并且它是等腰三角形ABC.

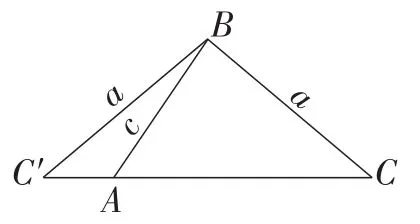
图9

师：好！还有不同意见吗？

生12：如图9，我发现当a＞c时，虽然△BCC′是等腰三角形，但是∠BAC′不是锐角了.所以，我认为此时也只能画出一个△ABC.

师：确实如此，另一个△ABC是不满足条件的！大家的发言都很精彩.下面小组合作讨论，总结、归纳这个问题.

生13：当a等于点B到AC的距离时，或者a≥c时，根据上述条件能且只能画出一个△ABC.当a小于c且大于点B到AC的距离，即d＜a＜c时，会画出两个不同的满足条件的△ABC.

师：很棒！通过画图，我们发现在特定条件下，SSA可以判定三角形全等.其中图7阐释了今天我们学习的HL定理.关于SSA的问题我们也终于彻底解决了.

案例中，由学生提出的一个质疑问题开始，教师设计与此问题有关的问题情境，变学生被动思维为主动思维.从生9一个不成功的图形开始，引导学生通过点C在直线AC上的不同位置进行有序探究，从而有效促进探索SSA判断全等三角形的条件.高阶思维的形成需要对问题的方案和结论存在的错误进行质疑和批判，并且引导学生进行思辨、创造，以生成可行的方案和正确的结论.为了使课堂指向高阶思维，教师在此环节中可以跟进以下两种策略.

第一，创建批判性氛围.教学中学生的质疑、批判也许说是与生俱来的，但批判性思维并不能由此而自然生长出来.只有当“批判”成为学习的一种习惯和一种生活方式，批判性思维才能应运而生.所以给学生创建批判性氛围，设计恰当的批判性问题，学生才能做到不盲从、不盲信，才能保持质疑与怀疑，才不会人云亦云.

第二，设计批判性问题.在动手操作画图的教学过程中，体验角θ的对边BC与邻边AB不同大小关系对所画图形的影响，进而感悟有序探究的思想方法.学生在活动、问题和对话中经历“质疑—猜测—操作—归纳”的过程，获得了分析、解决问题的成功体验和感悟，提升了学生的数学核心素养和思维品质.

四、编题、赏题，在创新与评价过程中指向高阶思维

思维的行为表现需要学生使用先前所学到的知识，形成新的观点、信息，在课堂上伴随着学生的设计、阐述、计划、修改、生成、建议、制作等行为.编题和赏题需要学生利用所学知识，观察、分析、研究自己在学习中遇到的问题，创造性地提出解决这些问题的方案.同时，需要对方案的合理性、有效性进行预测、分析和比较，以便做出鉴别、选择和改进.指向高阶思维的课堂就需要在课堂上打开学生的分析、评价、创造之窗.

环节4：编题、赏题环节设计.

教师从角平分线的模型中继续引发学生思考：若在AC上任取一点H，HE和HB有什么数量关系？

例题讲解：如图10，设∠ABC=∠AEC=90°，H是AC上一点，BC=EC，求证：EH=BH.

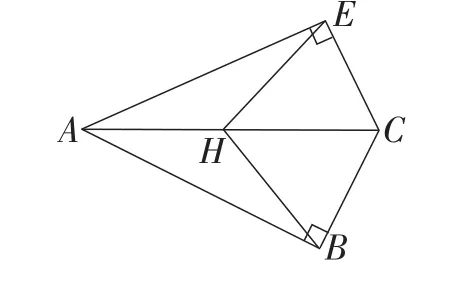
图10

本例是为了巩固两大定理而设计.解题的方法具有多样性，从用两次全等的证明，到用一次全等的证明，再到不用全等证明.教师引导学方法逐步深入，更显巧妙.

变式练习：如图11，点A，C，D在同一条直线上，∠A=∠D=90°，∠CBE=∠CEB，AC=DE，求∠BCE的度数.

图11

此练习题难度不大，主要是为了落实、巩固基础，由学生独立完成，教师巡视发现不足，投影展示.课堂中教师在例题讲解和变式练习之后，安排了如下编题、赏题环节.

我能编好题：小组合作——好题diy.

编题要求：①各小组利用给定的两个直角三角形拼成一幅基础图形，钉在KT板上；

②根据所拼的图形，设置条件，给出结论；

③根据出题的需要，可以在基础图形上增加线段、射线和直线等；

④要求证明其结论过程中要用到HL定理的知识；

我能评好题：我对________组编的题目进行评价.

①从条件（是否严谨，是否有重复、累赘或无用）看___________________________；

②从结论（结论能否证明，是否能够得出其他正确的结论）看_____________________；

③此题主要用了________________数学知识.

从前面的几个模型，引导学生发现其都是由两个直角三角形拼出来的，通过添加一些条件，可以得出不同的结论，相信学生也能编出优秀的题目.此环节主要让学生发挥创新能力、逻辑推理能力、小组合作能力、表达能力等.从编题到赏题，锻炼学生猜想、核查、评估、创造等技能，在运用高阶思维的过程中，问题解决相伴相生.为了使课堂指向高阶思维，教师在此环节中可以跟进以下两种策略.

第一，设计开放性问题.案例中，“我能编好题”环节能给所有学生示范一些知识、技能，提供理解的机会，为学生提供了进行超出能力范围的推理、思考的平台，从编题的反馈也能够看到学生使用广泛的解决方法和策略.孤立的、封闭的、结构良好的问题，局限了学生在新、旧知识上的串联与重组，很难引发学生展开反思、批判、创新等思维活动，必然达不到发展高阶思维的目的.而课堂中的“你能设计一个……吗？你能提出一个建议，将……吗？如果……，将发生什么？”等一些具有具挑战性问题更能打开学生的思维，使学生在思维“对话”和碰撞中活化所学的知识.

第二，提供“生生评价”平台.案例中，“我能评好题”环节能让学生对其他小组编写的题目的合理性和有效性进行分析评价，在找出不足和错误的同时，提出整改措施.这种生生评价的活动可以让学生对学习过程、学习思路、学习方法、学习策略展开深度咀嚼、反刍、总结、升华、拓展，从而培养学生的辩证思维能力和自我反思能力，加深学生对题目的理解，提高解题效率和能力.

美国教育家杜威曾指出，问题的本质决定了思考的结果，思考的结果控制着思维的过程.这一思维过程的本质即是高阶思维.围绕促进学生高阶思维能力的发展，已成为当代教育研究者最为重要的课题之一.因此，课堂教学不能只停留在课堂教学形态与内容的变革上，而应更多地关注课堂思维含量、思维品质和课堂效益等问题.本文仅仅围绕高阶思维展开相关的尝试、探索和反思，旨在抛砖引玉，还待有识之士进一步地实践研究.