深海半潜式平台与系泊系统动力耦合的边界约束效应研究*

2018-10-17范星宇杜君峰

中国海洋大学学报(自然科学版) 2018年12期

范星宇，杜君峰，刘勇

(中国海洋大学工程学院，山东青岛 266100)

为推进深远海油气资源的开发和利用，深海浮式平台系统的研究十分必要。随着水深的增大，系泊系统所受重力及环境荷载等也会增大，其与平台的耦合效应显著。因此，大型深海浮式平台与系泊系统的耦合作用不容忽视。

关于顶部浮体运动与系泊缆索动力响应的相互影响以及浮体与系泊系统整体耦合动力分析问题，国内外学者已开展了一系列的研究工作。Tcheou[1]，Ma等[2]，Lee等[3]，Yang和Teng[4]等通过研究指出：在深水条件下，传统的解耦分析或准静态分析可能会得到不可靠的结果。Kim等[5]运用时域方法，求得用线性无质量弹簧和非线性无质量弹簧模拟的系泊系统的运动和张力分布谱，研究平台主体与系泊索之间耦合效应对平台总体运动响应分析的重要性。DeKat等[6]，Ran等[7]，Chen[8]等均曾给出了耦合分析的详细计算过程，介绍了浮式生产系统及其挠性部件的整体耦合分析方法，并分别开展了系列研究。Low[9]等依据细长杆理论建立缆绳模型，采用耦合计算法在频域和时域内分别计算了浮式结构在规则波与随机波浪下的响应。肖越[10]分别采用间接时域法和直接时域Green函数法计算浮体的运动响应，然后与计算三维系泊缆索时域动力响应的非线性有限元法耦合得到了两种系泊系统的时域响应。易丛[11]、赵文斌[12]等考虑系缆所受到的海底接触力、流体拖曳力、惯性力、结构阻尼等因素，建立了Spar平台主体-系泊系统耦合运动方程，比较了全耦合方法和拟静态方法计算结果的差别。

考虑浮体与系泊系统边界约束，Berthelsen[13]将系泊系统简化为线性弹簧，对平台运动响应进行了相关研究。Johansson[14]将锚链固接于系泊浮体的一端，研究受迫运动后的动力响应，并且提出了一个用于耦合运动方程数值积分的新方法。Zhang和Zou[15]考虑立管和导向架间的作用，对Spar平台进行了的全耦合和部分耦合分析，在分析中模拟了带有真实边界条件的接触力。元志明[16]分别建立浮体、系泊缆索模型，并通过一系列的弹簧将浮体与系泊缆索耦合在一起，比较了全耦合分析、半耦合分析以及非耦合分析方法对半潜式平台结构运动性能预报结果的差异。王兴刚[17]假定上端点与浮体系缆点为理想铰接，研究了水深、波高、周期等对浮式结构物运动响应及系缆张力的影响。杨敏冬[18]考虑系泊缆索/立管与浮体的铰接边界条件，研究了波浪与整个系统非线性相互作用的耦合动态分析问题。袁梦[19]研究系泊缆索时，将锚泊线上端点通过导缆器与平台铰接，而对于立管，仅将上端在水平方向上进行约束，采用弹性支座理论。

综合国内外研究现状来看，浮体与系缆边界约束形式主要包括固接、铰接和弹簧连接三种，但目前对系统耦合动力特性进行研究时，均是直接采用某一种边界约束来开展工作，没有对比研究边界约束形式对系统整体动力响应的影响，也未给出所选取约束形式的适用性和合理性。因此，本文将研究不同边界约束对浮体/系泊整体系统耦合动力响应、系缆关键节点疲劳损伤等的影响，研究成果可为深海浮式平台及其系泊系统的设计分析等提供科学指导。

1 数值模型

基于SESAM软件建立深水半潜式平台分析模型，在频域内计算得到半潜式平台的水动力系数，进而通过时域耦合分析计算平台运动响应及系缆张力，并研究系缆关键节点的疲劳寿命。

1.1半潜式平台和系缆模型

本文以某深水半潜式平台为研究对象，作业水深1 000 m，排水量为51 849 t。主尺度参数如表1所示，该平台是典型的立柱支撑式半潜平台，主要由甲板、4个立柱、2个浮筒和4根水平横撑组成。根据表中参数建立平台模型(见图1)。

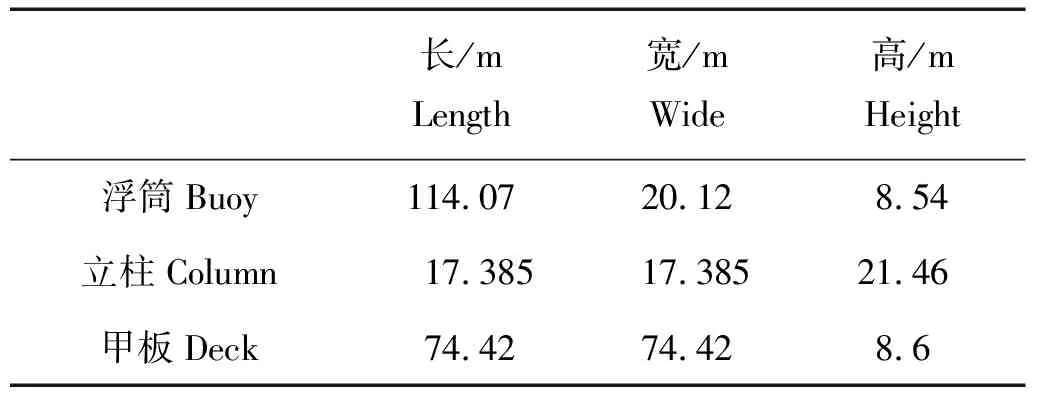
表1 半潜式平台参数表Table 1 Parameters of semi-submersible platform

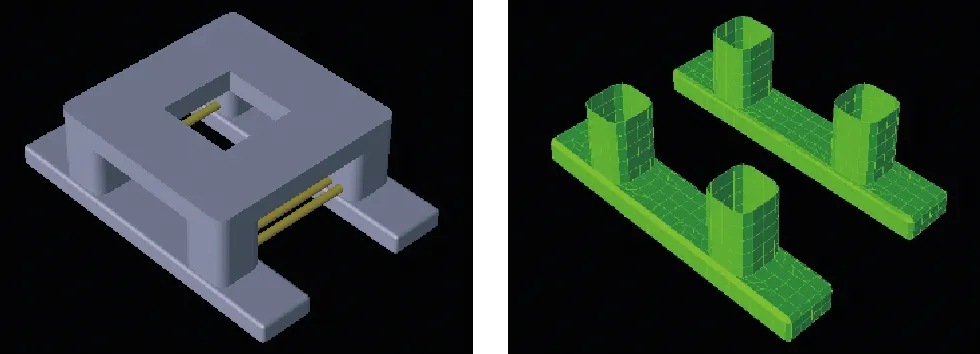
图1 半潜式平台数值模型图Fig.1 The numerical model diagrams of semi-submersible platform

半潜式平台的系泊系统为分组式系泊，共4组，每组3根。相邻组夹角为90°，每组内相邻两根系缆夹角为5°，图2给出了系泊系统布置的俯视图。为保证系泊系统具有足够刚度的同时质量较小，采用“锚链-钢缆-锚链”的分段张紧式系泊形式，其主要参数见表2。

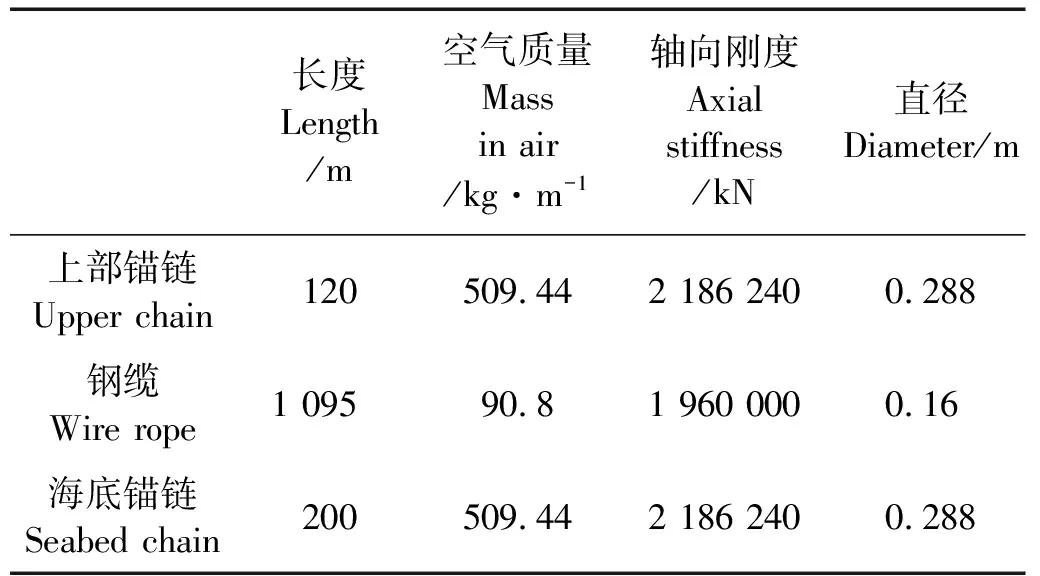
表2 系缆参数表Table 2 Parameters of moorings

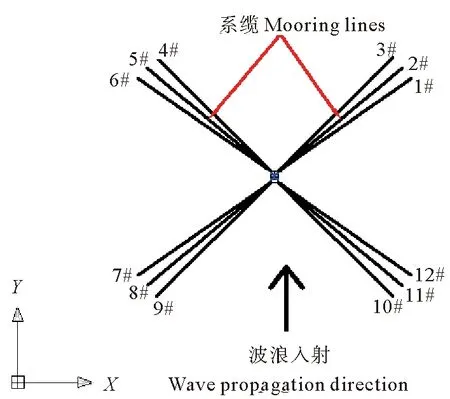
图2 系泊系统布置图Fig.2 The arrangement diagram of mooring system

1.2 边界约束模型

对平台与系缆的连接边界，分别采用固接、铰接和弹簧连接来模拟，对比研究不同的约束模型对浮体/系泊系统整体耦合动力响应和疲劳损伤的影响。3种边界约束模型如图3所示。

图3 边界约束模型图Fig.3 The model diagram of boundary constraints

固接是指系缆顶端与导缆孔通过一个锚链环连接，且该锚链环与平台导缆孔进行刚性连接，即6个自由度完全被平台约束。铰接是指不约束转动的3个自由度，将系缆上端点与导缆孔通过球铰连接。

弹簧连接是利用具有一定刚度和长度的弹簧来模拟系缆与平台的连接，描述导缆孔至平台甲板上部锚点之间系缆的受力与变形特征。依据实际锚链的力学特性，遵循弹性相似提出了弹簧刚度的设计准则

(1)

式中，F为该段系缆所受张力。根据该段系缆的长度lchain、刚度(EA)chain和弹簧的长度lspring(取一个锚链环长度)，则可对数值模拟中弹簧刚度(EA)spring进行设计。

2 边界模型对浮体/系泊整体系统响应的影响

2.1 时域耦合计算理论

考虑系泊系统与浮体耦合作用的运动方程表达式如下：

(2)

式中：[M]、[μ]、[λ]、[C]分别表示浮体的广义质量矩阵，附加质量矩阵，阻尼系数矩阵和静水恢复力矩阵；Fw(t)、FM分别表示波浪激励力和系泊力矩阵。

边界约束形式的不同则会影响系泊系统对浮体的作用力矩阵，即上式中的FM。系泊力矩阵FM可记为FM=[Fm,MM]T，Fm为系缆作用于浮体的力，Mm为系缆作用于浮体的力矩。

固接约束时，系泊系统对浮体的作用力为Fm，作用力矩为

Mm=[(r×Fm)+M′]。

(3)

其中：r为系缆上端点的位置；M′为锚链与浮体之间由于固接而产生的力矩。

铰接约束时，与固接相比，系泊系统对浮体的作用力矩有所变化，没有M′的作用。

弹簧约束时，系泊系统对浮体的作用力为

Fm=-[K](X+p+θ×p-r)。

(4)

其中：[K]为弹簧刚度矩阵；X是平动位移；θ是角位移；p是弹簧与浮体连接点位置；r是系缆上端点的位置。

系泊系统对浮体的作用力矩即为

Mm=p×Fm。

(5)

2.2 边界约束模型的验证

为验证三种边界约束的可靠性和合理性，将本文计算结果与某深水半潜式平台的物理模型试验结果[20]进行对比分析。在物理模型试验中[20]，系缆截断已经过静力和动力相似设计，试验过程中的平台模型参数、水深截断系泊缆索参数、不规则波参数也经过了校核，可确定模型试验能够得到较为准确的结果。

图4 导缆孔模型图[21]Fig.4 The model diagram of fairleads[21]

在物理模型试验中[20]，平台与系缆的连接边界采用实际工程中的约束形式，如图4所示。在数值模型中，平台与系缆的连接边界采用固接、铰接和弹簧约束3种形式。

选取物模试验测得的系缆张力的一组典型数据作为对比标准。数模分析时为验证弹簧刚度的选择，在弹簧约束下设置多个不同的弹簧刚度(假定由(1)式得出的刚度为EA，则选取0.01EA至100EA中多组数据)，分别计算其系缆张力的数值结果，并将其与模型试验测量结果进行对比，发现弹簧刚度为EA时，其数模结果与试验值最为接近。所以在数模分析中选择弹簧约束时，其刚度由1.2小节中(1)式的设计准则计算得出。

确定弹簧的相关参数后，在相应的工况下对固接、铰接和弹簧约束进行数模分析，对比系缆张力的模型试验测量结果和3种约束形式下的数值计算结果，如表3所示。

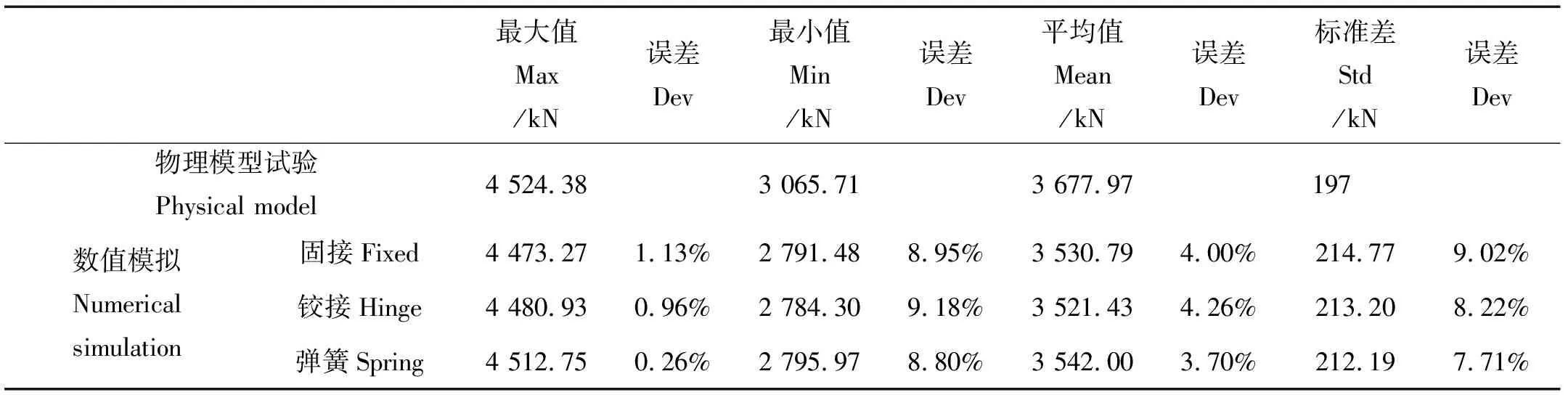
表3 数值模拟与物模试验系缆张力对比Table 3 The mooring tension comparison between numerical simulation and physical model test

由表3可以看出，与试验数据相比，数模分析中采用固接、铰接和弹簧约束会产生一定的误差，但三种约束下系缆张力的误差均不超过10%，均具有较好的预测精度。但整体而言，弹簧连接的预测精度是最高的。

2.3 不同边界约束下系统耦合动力响应的比较

选取平台作业海域中发生概率较大的波浪工况来研究，有效波高Hs=4.5 m，谱峰周期Tp=9 s，波谱为Jonswap谱。取浪向角θ=90°，即平台受到来自横向的波浪作用，如图2所示，处于最大横向受力状态。

计算三种边界约束形式下系统的耦合动力响应，锚链设置相同的预张力，均为53 500 kN。其中，弹簧约束形式的刚度遵循1.2小节中(1)式的设计准则，止链器和导缆孔之间的锚链长度lchain为27.06 m、刚度(EA)chain为2 186 240 kN，弹簧长度lspring为0.96 m，所以计算可得弹簧刚度(EA)spring为77560.6 kN。为能充分描述不规则波及其作用下结构系统动力响应的随机特性，对每个工况的数值模拟时间采用工程上建议的10 800 s。

在横浪作用下，平台纵荡、纵摇、艏摇三个自由度的响应较小，本文重点关注平台横荡、横摇、垂荡和系缆张力，其响应时历曲线见图5～8，相应的统计数据如表4所示。

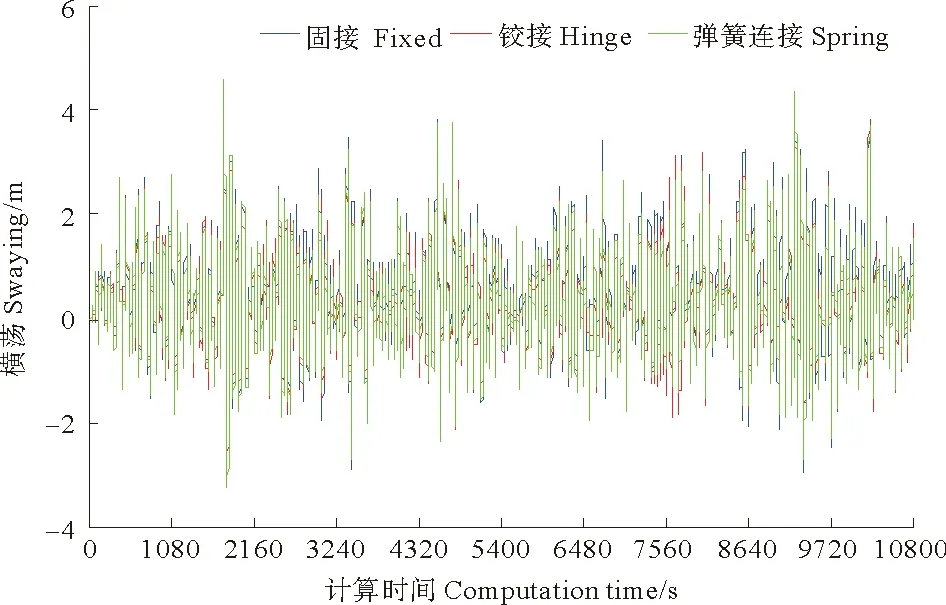
图5 横荡时程比较图 Fig.5 The comparison diagram of swaying time history

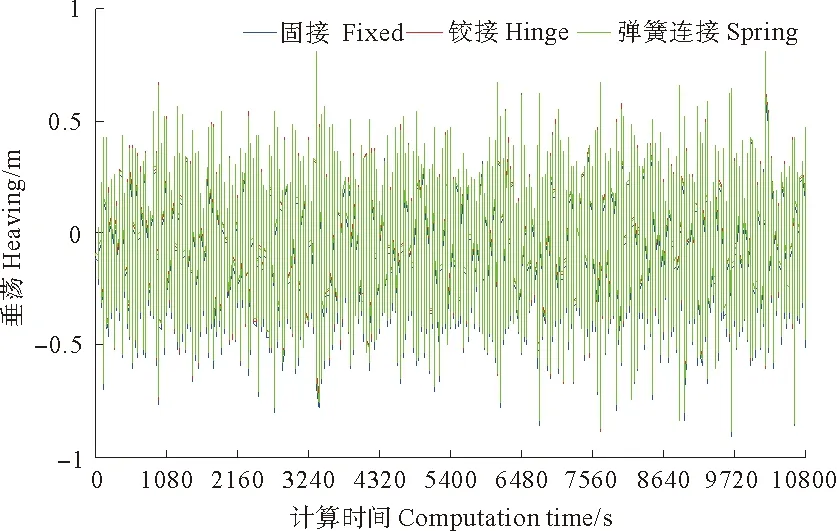
图6 垂荡时程比较图Fig.6 The comparison diagram of heaving time history

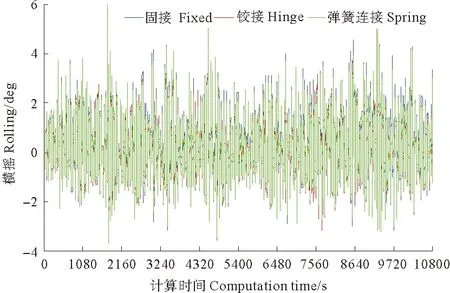
图7 横摇时程比较图Fig.7 The comparison diagram of rolling time history

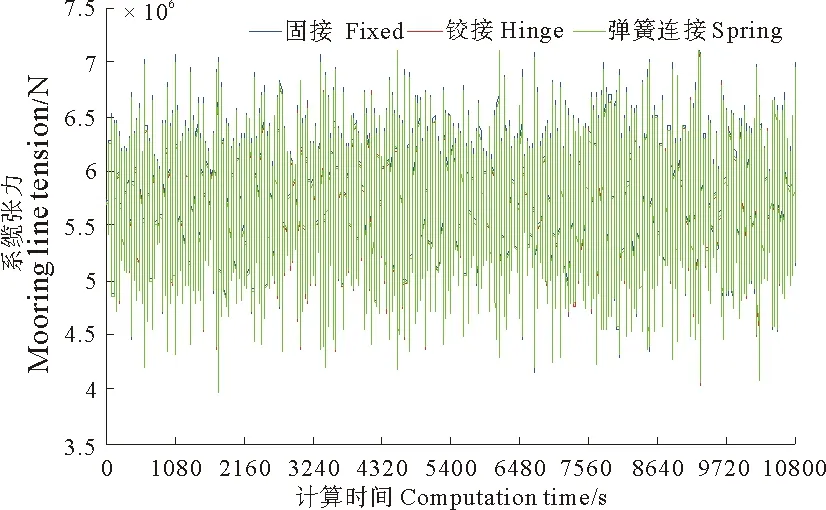
图8 1#系缆张力时程比较图Fig.8 The comparison diagram of 1# mooring tension time history

由表4分析可得，3种约束形式下的耦合动力响应计算结果比较接近。不同方法运动幅值的计算结果相差不超过5%，不同方法系缆张力的计算结果相差仅在2%左右。

系泊缆索是细长的柔性结构，改变平台与系缆连接边界的约束形式对系缆整体刚度矩阵影响不大，因此不同的边界模型对平台/系泊整体动力响应(平台运动和系缆张力)影响不大。但约束模型的改变可能会对系缆局部节点所受应力产生较大影响，因此接下来对系缆节点的疲劳损伤做进一步的研究。

3 边界模型对关键节点疲劳损伤的影响

3.1 疲劳损伤计算理论[22]

海洋工程结构疲劳损伤评估的基本步骤如下：

(1)对波浪散布图中每一组海况，用有效波高Hs和Tp谱峰周期定义不规则波，遍及所有海况，进行时域耦合动力分析，得到系缆张力(弯矩)时程，并计算系缆应力时程；

(2)依据数据统计法则(本文采用雨流计数法)，统计出系缆应力幅值及其对应的循环次数；

(3)结合S-N曲线以及Miner线性疲劳累积损伤法则，对系缆年疲劳损伤率和疲劳寿命进行评估。

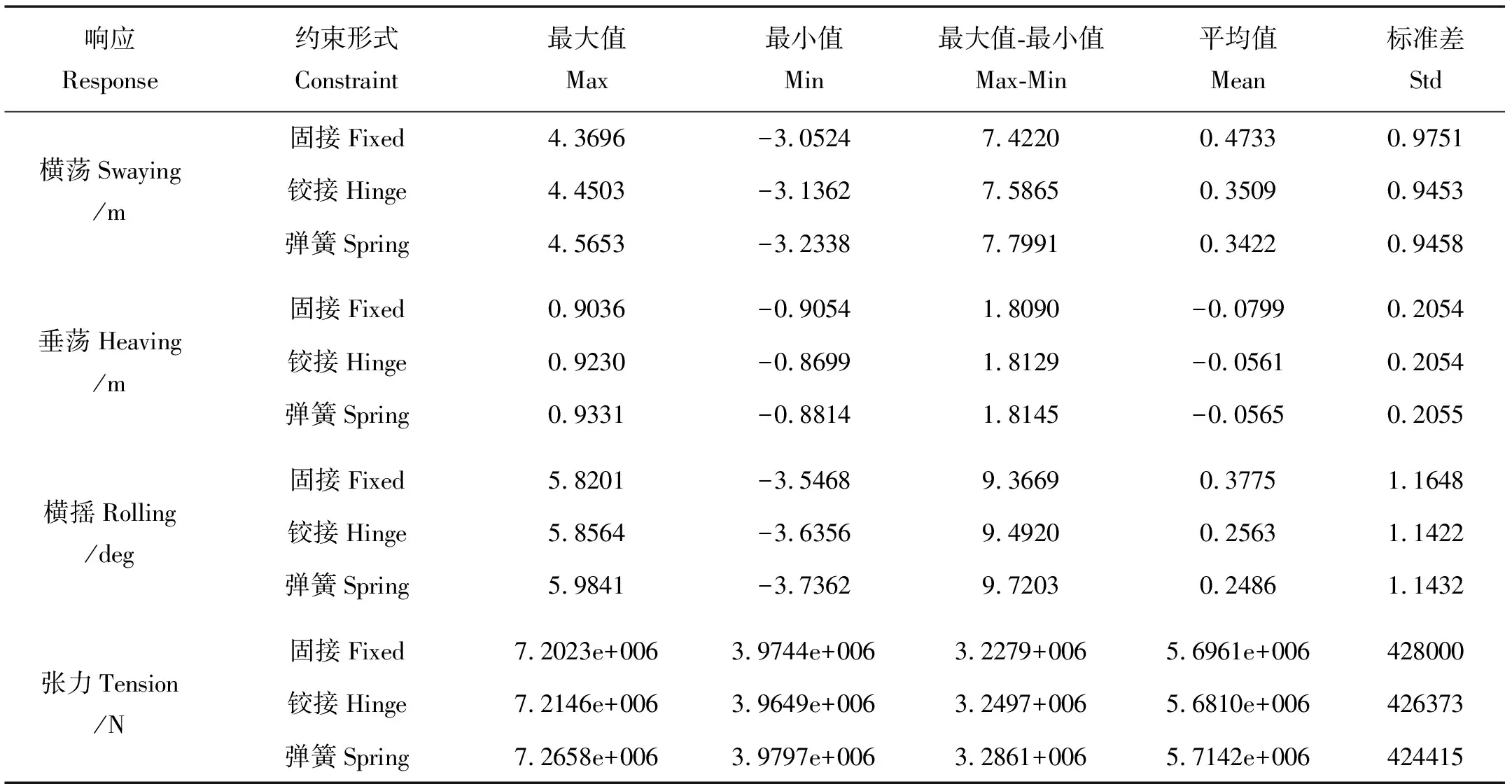
表4 响应数据统计表Table 4 The statistical result of response data

由于很多因素会影响S-N曲线的选择，计算时难以给定每种具体情况下的S-N曲线，所以绝大多数船级社选用已有的试验成果来确定该曲线。本文选用DNV规范提供的S-N曲线进行疲劳损伤分析，形式如下[23]：

(6)

其中，Δσ为应力幅值；N为相应于应力幅值的预期疲劳循环次数；loga为S-N曲线在Y轴上的截距；m为S-N曲线的斜率；tref为参照壁厚，非管节点连接一般取25 mm；t为裂纹最可能生长的贯穿长度，小于tref时，取t=tref；k为疲劳强度壁厚指数。

根据DNV规范选择B1曲线来计算系缆的疲劳损伤[24]，具体参数见表5：

表5 B1曲线相关参数Table 5 Related parameters of the curve

Miner线性疲劳累积损伤法则：

对于结构受变幅交变应力作用的情况，结构总的疲劳损伤量可以通过把各不同的应力循环造成的疲劳损伤按线性的原则累积得到。当结构总的疲劳损伤量达到某一数值时，就将发生疲劳破坏。Miner线性累积损伤理论认为：某个应力范围的实际循环次数与该循环应力作用下达到疲劳破坏所需的循环次数之比即为该应力范围造成的损伤分量。

3.2 不同边界约束下系缆关键节点疲劳寿命的比较

海域长期的波浪条件通常采用波浪散布图来表示，如表6所示为平台作业海域的波浪散布图数据，每个海况用波浪的特征参数和该海况出现的频率加以描述。对波浪散布图中的每个海况分别进行计算，得到其导致的系缆疲劳损伤，然后进行求和得到结构总的疲劳损伤。

浮式结构在波浪作用下，往往会产生较大的运动，这些运动响应主要包括一阶波频和二阶低频成分，它们构成了浮体水平运动的主要部分和升沉运动。以1#系缆为例，依据上表海域的波浪分布，通过时域耦合动力分析，再结合S-N曲线和Miner线性疲劳累积损伤法则，分别计算考虑二阶慢漂和不考虑二阶慢漂时固接、铰接和弹簧连接这三种约束条件下系缆关键节点的疲劳损伤。其中，所取关键节点均在系缆上部锚链段，节点1为该段锚链上端点，节点2为距上端点30 m处，节点3为距上端点60 m处，节点4为距上端点90 m处，结果见表7和表8。此外，还给出了表8和7相对应节点疲劳寿命的比值，如表9所示。

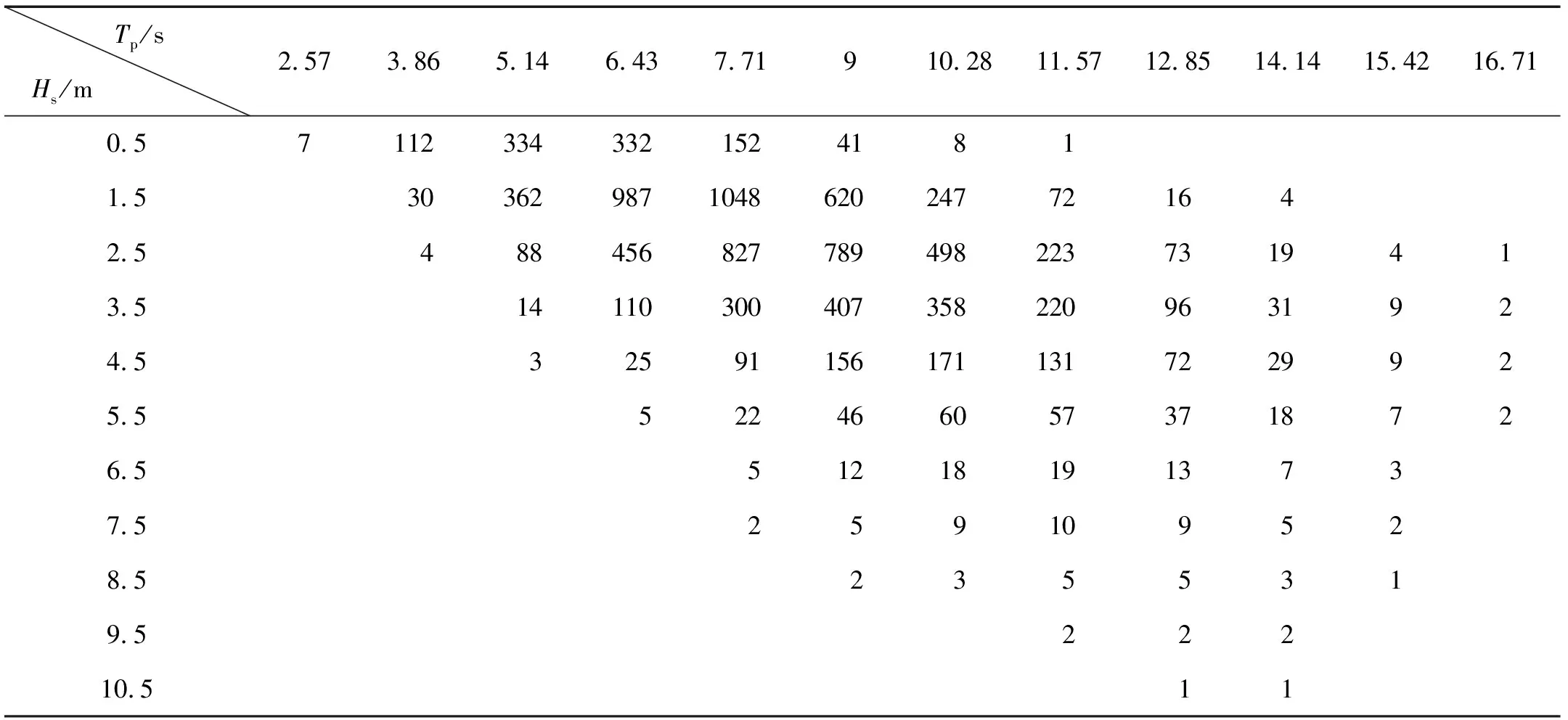
表6 作业海域波浪散布图Table 6 The waves scatter diagram of operation waters

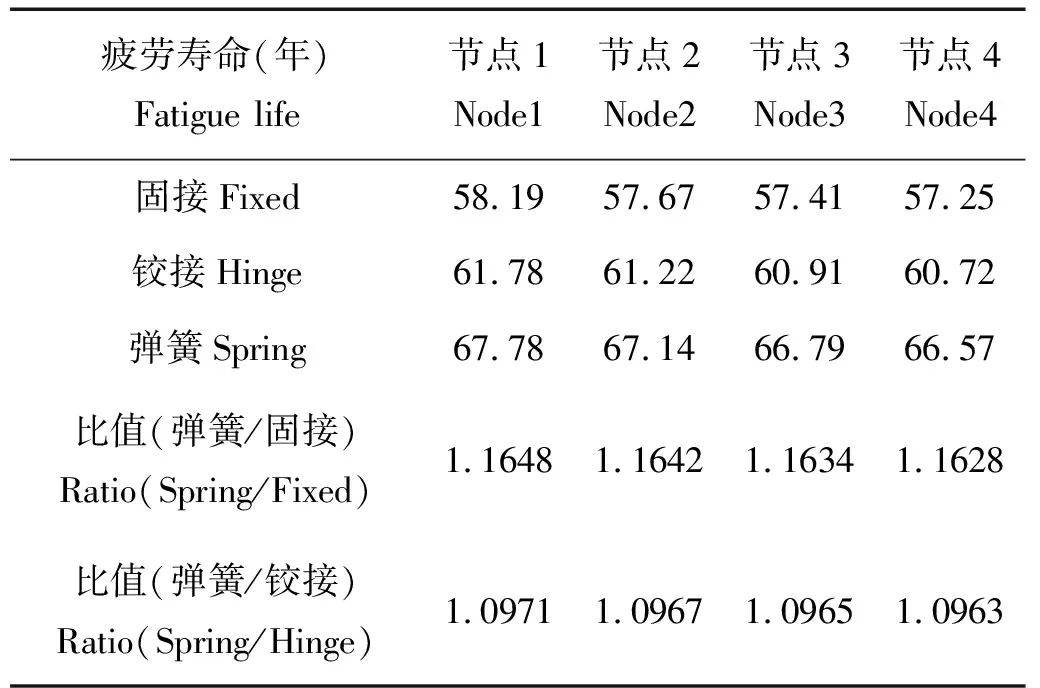
表7 考虑二阶慢漂时节点的疲劳寿命Table 7 The nodes fatigue life with considering the second order slow drift

表8 不考虑二阶慢漂时节点的疲劳寿命Table 8 The nodes fatigue life without considering the second order slow drift

表9 不考虑二阶慢漂与考虑二阶慢漂对应节点疲劳寿命的比值Table 9 The ratio of corresponding node fatigue life when considering or not the second order slow drift

3.3 计算结果分析

(1)约束条件的影响

由表7、8可知，三种边界约束下相同节点的疲劳寿命存在差异：

考虑二阶慢漂时，弹簧连接下节点的疲劳寿命最高，铰接次之，固接最低，弹簧约束比铰接高约10%，比固接高约16%。因为在平台做大幅慢漂运动时弹簧可以起到缓冲调节的作用，其张力幅值较小，对应锚链的疲劳损伤最低，寿命最高。

不考虑二阶慢漂时，铰接和弹簧约束下节点的疲劳寿命相差不到1%，比固接高约6%。因为不考虑大幅慢漂，平台正常运动时，与固接相比，铰接和弹簧连接下平台导缆孔与系缆上端点相互作用较弱，系缆在耦合作用下的运动和受力幅度较小，所以疲劳损伤也就较小。

更直观地，由表9数据可以看出：不考虑二阶差频效应时，三种约束形式下系缆的疲劳寿命均变大，其对固接和铰接方式系缆疲劳寿命影响较为显著，约增大22%，而对弹簧连接形式的影响相对较小，增大11%左右。

(2)系缆节点位置的影响

将表7、表8中数据进行横向对比分析可得，对于上部锚链段，节点由上至下，即由节点1到节点4，在同种边界约束下节点的疲劳寿命逐渐减小，且边界约束形式的改变对节点疲劳寿命的影响也越来越小。

系缆采用“锚链-钢缆-锚链”的分段形式，由于锚链与钢缆的直径、质量、刚度等方面存在的差异，在耦合运动中，锚链与钢缆的连接点处运动最为剧烈，受力幅值最大，导致疲劳损伤最大，寿命最短。所以，对上部锚链段而言，越靠近锚链与钢缆连接处，节点的疲劳损伤越大，寿命越低。同理，对于钢缆段和海底锚链段也是如此[21]。因此，在上部锚链段，由节点1到节点4疲劳寿命逐渐减小。

此外，弹簧与固接、弹簧与铰接的比值随着节点由上至下逐渐减小(比值小于1时逐渐增大)，说明边界约束形式的改变对节点疲劳寿命的影响也随着节点由上至下越来越小。因为本文研究的边界约束模型是处于导缆孔与系缆上端点之间，改变其约束形式对连接处附近系缆节点的受力状态影响较大，而对远离连接处的系缆节点影响较小。