基于谱分解的广义岭回归方法及其优良性探讨

周 涌

(湖北科技学院 数学与统计学院，湖北 咸宁 437000)

一、引言

(一)广义岭回归问题的产生

基于高斯—马尔科夫假定的多元线性回归模型为：

(1)

对于未知参数β，其普通最小二乘估计为：

要让这个估计存在，必须要求X′X可逆，这相当于要求设计矩阵X是满秩的，否则称模型(1)具有多重共线性特征。多重共线性普遍存在于现实数据中，它会导致X′X=0，使得其逆矩阵不存在，也就无法获得普通最小二乘估计[1]113-137；即便X′X≠0，但非常接近于0，也会有害于参数估计，这是因为：

岭回归方法最早由Hoerl于1962年提出[2]，用于当存在多重共线性状况时，对最小二乘估计量进行改进。1970年，Hoerl和Kennard在两篇论文中详细探讨了岭回归方法[3-4]。该方法的主要思想是：当X′X≈0时，给其加上单位矩阵的正常数倍，使得X′X+kI远离0，从而使得X'X+kI可逆，此时最小二乘估计量相应地调整为：

(2)

其中常数k被称为岭参数，而矩阵kI被称为调整矩阵。在Hoerl和Kennard之后有学者提出：调整矩阵不必限定于kI，可以是QKQ′，其中K是一个主对角线上元素非负但各不相同的对角矩阵，K=diag(k1，k2，…，kr)，Q为X′X的单位正交特征向量组成的正交矩阵[5]，这时参数估计值相应地变为：

(3)

这种方法被称为广义岭回归(为了便于区分，以下将Hoerl提出的岭回归方法称为狭义岭回归)，可以证明：广义岭回归参数估计量(3)比狭义岭回归参数估计量(2)，具有更小的均方误差[6]81-127。

(二)相关研究的最新进展

作为一种被广泛使用的数据分析方法，回归分析在许多领域发挥了重要作用，对其的改进也随着应用的发展而不断深入，其中特殊条件下回归分析的统计性质以及多变量问题成为研究重点[7-8]。近年来，在广义岭回归的理论方面，许多学者进行了大量研究，得到了一些基于特定优良性指标的好的估计量，可容许广义岭回归、半参数广义岭回归等方法相继被提出。随着计算机技术的发展，学者开始通过算法研究对广义岭回归进行改进，提出了利用神经网络算法来确定模型参数，但又发现该方法存在过拟合等缺陷[9]；Beam等学者提出利用基于支持向量机回归算法来改进神经网络方法的缺陷，并取得了不错的效果，但也未在不确定性参数的优化选择领域取得突破性进展，而这些估计量大多是非线性估计，其统计优良性远不如线性估计量，广义岭回归理论并没有显著的突破[10-11]；Vapnik提出干脆放弃对估计量的线性要求，退而求其次地在非线性估计量中寻求优良性估计量[12]47-96。

本文将提出一种在计算上简便易行的广义岭回归方法，使得该方法的实用性大大增强，同时能保证参数估计量是线性的，从而具有线性估计的一切优良性。

二、广义岭回归方法的缺陷

为了方便寻找K*，引入线性回归模型(1)的典则形式：

y=Zα+ε

(4)

其中Z=XQ，α=Q′β，Q为X′X的单位正交特征向量组成的正交矩阵。基于典则形式的式(4)的参数最小二乘估计为：

由于β=Qα，相应的β估计量为：

当基于模型(1)的广义岭回归估计量为式(3)时，相应的典则参数α的广义岭回归估计量为：

可以证明

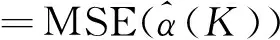
(5)

上述结果直接导致了广义岭回归的两大缺陷：

其一，σ2和αi都是未知参数，需要通过估计才能得到，而二者常用的较优良的估计量都与y有关，这就导致广义岭回归估计量式(3)不是y的线性变换，也就不再具备线性估计量的任何优良性。

三、基于谱分解的广义岭回归方法

岭回归以及广义岭回归的实质，都是在X′X不可逆或近似不可逆的情况下，通过给X′X加上一个调整矩阵A，使得X′X+A远离病态性，这时估计量为：

其对应的协方差矩阵为：

岭回归的目的就是在一定程度上牺牲估计量的无偏性，保障其有效性，即将估计量方差控制在一定范围之内。传统广义岭回归方法在处理这个问题时，要求矩阵(X′X+A)-1X′X(X′X+A)-1主对角线上的元素不能太大，这等价于要求X′X+A的所有条件数都不太大，通常的要求是不大于10。本文将提出一种新的广义岭回归方法，该方法得到的估计量的优良性在于：一是该估计量是线性估计量；二是在将协方差矩阵都控制在合理范围之内时，本估计量比传统岭回归具有更小的均方误差，这一点将在第四节通过数据模拟来验证。以下说明本估计量的构造思路：

以上分析引出了一种新的构造调整矩阵A的思路，即将矩阵X′X进行谱分解得到：

其中λ1≥λ2≥…≥λr≥0为全部特征根，li为相应的正交单位特征向量；X′X病态程度较高时，必有一个以上特征根小于最大特征根的1%，不妨将其记为λs+1≥λs+2≥…≥λr≥0，这时取：

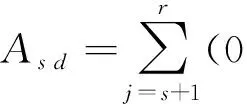
为调整矩阵，则：

也就是将X′X中小于0.01λ1的特征根都加大到0.01λ1，其他的都不变。 容易证明：矩阵X′X+As d的全部特征根为λ1≥…≥λs>0.01λ1=…=0.01λ1>0，li依然为相应的单位正交特征向量，此时矩阵X′X+As d所有条件数都不大于10，不再具有病态性。由于：

=Qdiag(0，…，0.01λ1-λj，…，0.01λ1-λr)Q′

这等价于在(3)中取K=diag(0，…，0.01λ1-λj，…，0.01λ1-λr)，故以这样的As d为调整矩阵，仍属于广义岭回归的范畴；又由于As d是基于X′X进行谱分解得到的，因此命名为“谱分解广义岭回归法”。

谱分解广义岭回归法具有以下优良性：

第一，计算极其方便：计算量不仅远远小于一般广义岭回归法，也小于狭义岭回归方法。狭义岭回归在确定岭参数k时，需要进行岭迹分析等复杂计算，还要兼顾参数估计值的符号正负性与实践意义是否相符；一般广义岭回归算法需要通过回归模型的典则形式过渡，并以某些其他参数估计值为前提基础、才能得到参数估计量[13]76-134；谱分解广义岭回归法的计算量则相对小得多，且省去了狭义岭回归的岭迹分析或广义岭回归的典则变换等繁冗环节，实用性大大增强。

第二，线性估计量：基于谱分解广义岭回归法得到的调整矩阵As d，只依赖于对X′X的谱分解结果，与y无关，因此相应的参数估计量是线性估计量；而广义岭回归不具有此优良性，即便是狭义岭回归法，其调整矩阵kI看似与y无直接关联，但在确定岭参数k时却需要y的间接参与，因此得到的也不是线性估计量[14]，在这个方面谱分解广义岭回归法具有先天优势。

四、数据模拟

在上一节中，提出了“谱分解广义岭回归”方法，得到了一种新的调整矩阵的导出方法，并指出该方法具有计算方便、估计量为线性以及估计误差小等优良性。对于前二者，在上一节已经做了阐述，本节验证第三个优良性，即比狭义岭回归估计量具有更小的均方误差。

步骤一寻找3个无多重共线性的自变量样本数据并进行标准化，标准化后变量记为x1,x2,x3。

步骤五取非零常数向量β=(b1,b2,b3,b4,b5)′，令y=b1x1+b2x2+b3x3+b4x4+b5x5+ε3生成新变量y的样本数据，ε3为0均值正态分布的随机数。

上述样本数据模拟过程步骤一、三、四保证了回归模型具有多重共线性；步骤五则提供了模型的模拟系数真实值，以下将其作为真实值看待。依照上述步骤，得到了一组容量为75的模拟样本数据(其中β=[2，0.8，-3，0.5，-1.2]′)，见表1。

以上得到了模拟样本数据，以下开始验证：

第一步，对上述样本数据进行狭义岭回归参数估计：利用SPSS软件中的岭回归模块，可以得到狭义岭回归的一个较理想岭参数为k=0.011，对应的系数估计值为：

1.161 0 ]′

第二步，对上述样本数据进行谱分解广义岭回归参数估计：对X′X进行谱分解，得到的特征根从大到小依次为46.384 5、27.19、1.232 2、0.202 3、0.012 7，对应的单位正交特征向量分别为：

l1=[ 0.589 8 -0.461 4 0.012 4 -0.662 5 0.015 8 ]′

l2=[ 0.012 8 -0.043 6 -0.683 6 0.046 4 0.726 9 ]′

l3=[-0.392 8 -0.676 0 0.463 4 0.139 1 0.393 3 ]′

l4=[-0.655 7 0.202 0 -0.057 2 -0.725 1 0.016 2]′

l5=[ 0.260 3 0.536 2 0.560 8 -0.117 7 0.562 5 ]′

后两个特征根小于最大特征根的1%，需要增大0.463 845，因此调整矩阵为：

对应的系数估计值为：

-0.461 9 ]′

第四步，将上述模拟过程重复多次，若一次模拟试验中谱分解广义岭回归估计值的均方误差小于狭义岭回归估计值，则该次试验结果记为1，否则记为0；笔者在实际操作中重复了百余次，每次模拟的样本容量不尽相同，介于50～100之间；统计试验结果为1的频率，其结果显示为100%，即全部试验无一例外地显示：谱分解广义岭回归估计值的均方误差小于狭义岭回归估计值的均方误差，最小的一次仅为后者的7.73%；依据蒙特卡罗原理，可以认为在达到同样的方差控制效果时，谱分解广义岭回归估计值稳健地比狭义岭回归估计值具有更小的均方误差。

表1 样本数据模拟结果表

五、小结

对线性模型回归系数的LS估计量，在误差服从正态分布的情况下，在一切无偏估计类中具有最小方差；但当X′X接近奇异时，LS估计量的方差却非常大，导致估计精度低且稳定性差。狭义岭回归与广义岭回归正是解决这一问题的有力工具，能大幅度降低估计量方差，但同时也带来了估计量非线性、计算过程繁杂等缺陷。为了克服狭义岭回归和广义岭回归方法中的一些固有缺陷，本文提出了一种基于谱分解的调整矩阵的算法，即通过该方法可确定调整矩阵，无需借助于因变量的任何样本数据信息，因此得到的估计量是线性估计量，同时该方法的运算简单易行，比传统方法更具有实用性。

由本方法得到的调整矩阵满足传统的广义岭回归对调整矩阵的规范形式的要求，因此本方法仍属于广义岭回归的范畴，本质上是一种对LS估计的非均匀压缩；但是与狭义岭回归和一般广义岭回归不同的是，本方法只在少数几个方向上进行压缩，而不是全面压缩，因此对LS估计量的改动幅度并不大，在消除共线性的同时产生的偏差却尽可能地小，也就具有了非常小的均方误差。