基于相似度量强化的容差水平软集决策方法

李长仪，管建和，刘婷婷，张立涛

(1.中国地质大学(北京) a.经济管理学院，b.信息工程学院，北京 100083；2.山东理工大学 管理学院，山东 淄博 255000)

一、引言

当前，伴随决策理论方法研究的不断深入，随机、含混及非精确的决策形态成为该领域的重点突破方向[1-2]。在各类不确定理论纷纷介入求解的基础上，Molodtsov以参数化架构确立的软集理论为这一问题的研究带来了全新视角[3]。与此同时，其与不确定理论的交叉渗透进一步丰富和拓展了相应的理论与实践体系，形成了融合发展之势。

软集理论的模糊化扩展作为这一潮流的典型代表，自Maji确立模糊软集概念以来，诸多学者就对其多种形态的数理规范及决策应用进行了广泛研究。而Maji和Roy基于经典软集决策确立的选择值策略成为模糊软集决策研究的重要思想基础和方法支撑[4]。就现有工作而言，基于模糊软集的决策方法可归纳为以下四种类型：

一是基于参数对比的决策方法。Roy和Maji于2007年提出了这一策略，是根据模糊软集论域中各对象在相应参数上的大小比较关系而实现的决策排序[5]。之后多位学者的决策方法研究中也遵循了这一思路[6-7]。该方法契合了模糊软集的参数化架构及研究视角，但以排序换算得分的做法使得优劣参数直接互补，易于产生非均衡决策；此外，该方法的计算复杂度依赖于论域对象的稳定性。

二是基于参数值集成的决策方法。这一策略是应用各类模糊数集成算子对论域对象的参数值进行集结，产生模糊选择值以实现决策排序。它最早源于Kong对Roy和Maji参数对比方法的质疑[8]，而后Deli、Chen、Xiao、Das、武华等则应用多型模糊数集成算子进一步贯彻了该决策思想[9-13]。但当前研究主要集中在数理运算上的有效性，而对决策领域所关注的科学性、均衡性、现实性并未过多涉及。

三是基于水平软集的决策方法。Feng在2010年提出运用给定阈值将模糊软集转化为精确软集(水平软集)，然后以经典软集的选择值执行决策排序的策略[14]。随着众多研究的持续跟进，它成为该领域最具代表性的决策手法。该方法秉承了经典软集的决策思想，在保持参数独立性的同时实现了简洁、高效、均衡决策。但也存在以下问题：模糊程度化信息完全丢失；阈值刚性导致认知两极分化；分辨能力有限。

四是基于相似度量的决策方法。Xiao、王浩伦、Muthukumar、Zhang等定义了多型模糊软集的相似性，并将其应用于决策之中[15-20]。其基本原理是基于模糊(软)集的相似性定义，对论域对象与理想解的相似程度进行衡量，以之实现决策排序。相似度量的策略摆脱了参数各自独立的纬度束缚，但可加性一定程度上也带来了参数表现的互补，故该方法应用中要防范“注重整体效用，忽视个体缺陷”的决策风险。

通过对模糊软集决策方法的总结，本文基于容差柔化的水平软集决策思想，结合重点论域对象的相似度量分辨，从而构建基于相似度量强化的容差水平软集决策方法，以实现高效、均衡及高分辨性能的决策。

二、预备知识

关于软集、模糊软集及水平软集的基本概念与实例介绍如下。

(一)软集与模糊软集

假设U为研究对象的初始论域，EU(简记为E，称为参数空间)是与U中对象有关的所有参数的集合。于是，(U,E)又被称为一个软论域。

令P (U)为论域U的幂集，而A⊆E为参数集，则软集可定义如下：

定义1[3]二元组S=(F,A)称为论域U上的一个软集，其中，F：A→P (U)是一个集值映射，称为软集的近似函数。取参数e∈A，则F(e)⊆U。

在此基础上，Maji等将模糊集理论与软集相结合，于是便产生了如下的模糊软集定义。

令F (U)为给定论域U上的全体模糊子集，E为参数集，且A⊆E。则：

例1 假设U为在售计算机的集合，且U={c1,c2,c3,c4,c5}，而E为计算机评价指标形成的参数集，E={e1/价格便宜,e2/质量可靠,e3/性能优越,e4/易于操作,e5/售后完善}。

模糊软集F1也可以如表1所示的表格化形式进行描述。

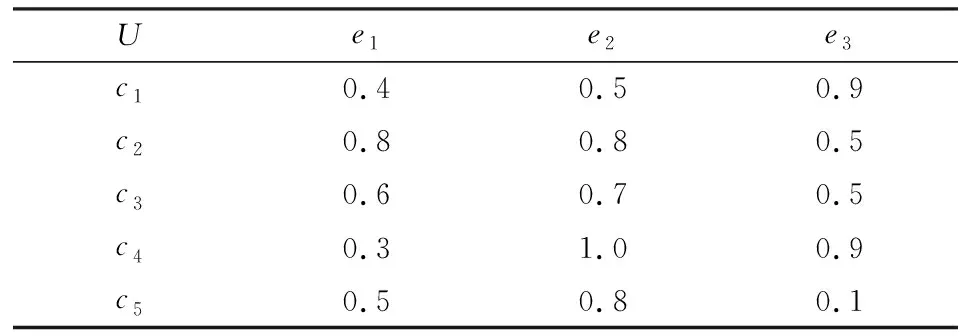
表1 模糊软集F1的表格化形式

由此可见，作为软集模糊化扩展的模糊软集，不再局限于精确软集对对象参数的0或1的简单描述，而是以更为灵活的0、1间的模糊形式表达参数隶属程度，从而使其能被广泛应用于各个领域的不确定状况。

(二)水平软集

在现有大量模糊软集决策方法的研究中，Feng提出的水平软集策略得到了广泛关注和认可。相关定义如下：

定义3[14]精确软集L(F；λ)=(Fλ，A)定义为模糊软集F基于其阈值模糊集λ的水平软集。其中，近似函数Fλ：A→P(U)定义为：

基于以上定义可以看出，水平软集是通过一个模糊集对原有模糊软集的隶属度进行辨识从而转化产生的精确软集。

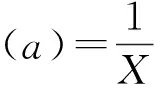
表2 模糊软集F1的均值水平软集

三、决策方法设计

本章在定义容差水平软集的基础上，设计了基于水平软集及其容差水平软集的决策方法，然后通过相似度量对分辨能力予以强化。

(一)容差水平软集

定义4对于模糊软集F，定义精确软集L(F；θ)=(Fθ，A)为关于水平软集L(F；λ)=(Fλ,A)的容差水平软集。其中，近似函数Fθ：A→P(U)定义为：

其中，θ(a)=λ(a)-ρ(a)，而ρ(a)称为参数a的水平容差，且0≤ρ(a)≤λ(a)。

表3 模糊软集F1关于的容差水平软集

(二)水平软集筛选

考虑到水平软集决策中阈值刚性所带来的判断偏差，以水平软集结合其容差水平软集共同产生方案备择集。

给定论域U和参数集A，且U=m，A=n。对于其上构建的模糊软集F，根据定义3和4分别得到其水平软集Sλ和对应容差水平软集Sθ。

于是，决策方案的备择集D构建如下：

需要注意的是，如果各参数被赋予了相应的权重，则以权重值取代水平软集表格形式中的1进行选择值汇总。

(三)相似度量强化

对于上一节中的模糊软集F，令其表格化形式的表达矩阵为F=(fij)m×n。

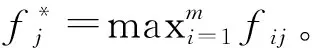
于是，上一节中备择集D包含的对象xi对理想解的相似度量执行如下：

(1)

若对应参数aj(j=1,2,…,n)，存在权重ωj(j=1,2,…,n)，则相似度量计算为：

(2)

最后，根据相似度量值Si对备择集D中的对象进行排序，最大者作为最终的决策方案。

四、算例分析

基于网络化制造供应商选择问题对本文的决策方法进行了验证。其中的参数架构既包括传统模式下供应商的基础评价指标，还纳入了体现其网络化运作性能的专项指标。

本例以网络化制造平台上某次任务的全体竞标供应商为集合U，且U={s1,s2,s3,s4,s5,s6}，而由相关供应商选择指标所形成的参数集合为E={e1/价格便宜,e2/质量可靠,e3/准时交货,e4/技术先进,e5/财务良好,e6/经验丰富,e7/柔性定制,e8/敏捷响应,e9/伙伴协同,e10/信誉良好}，另有参数权重集合W={ω1=0.11,ω2=0.13,ω3=0.12,ω4=0.10,ω5=0.10,ω6=0.09,ω7=0.10,ω8=0.08,ω9=0.09,ω10=0.08}，其中，ωj为参数ej的权重(j=1,2,…,10)。

取参数子集A=E，通过历史数据统计、客户反馈、专家评价等多种渠道分别获取的各参数信息构建供应商选择的模糊软集F2(表格化形式如表4)，相应得到其表达矩阵F2。

表4 模糊软集F2

最终，决策方案选择s5。

表5 F2的均值水平软集

表6 F2关于的容差水平软集

表7 备择集D2中对象对理想解的相似度量

五、典型方法对比

应用引言所述典型模糊软集决策方法，以模糊软集F2及参数权重为前提，对网络制造供应商的选择问题进行决策，然后将它们的决策性能与本文提出的方法进行对比和分析。

(一)参数对比方法与参数值集成方法

Roy和Maji提出了比较表方法进行模糊软集决策，但其中并未涉及参数权重应用的讨论[5]。在此，对该方法做如下调整：将其中对比后的占优参数计数以对应参数权重和予以代替。然后得到行和ri及列和ti，并以相应行和与列和的差产生得分值si。最终，构建如表8所示的比较表。根据得分值si排序为：s3>s5>s1>s6>s2>s4。于是，该决策结果为供应商s3。

基于Kong的模糊选择值决策方法对模糊软集F2执行决策[8]，可得如表9所示的各供应商模糊选择值ci。根据模糊选择值排序为：s3>s5>s1>s6>s2>s4。于是，该决策结果同样为供应商s3。

通过对供应商的参数表现进行分析，可以看出：虽然s3大多数参数具有很高隶属度，但存在明显缺陷参数e3，而s5虽各参数隶属度并不绝对突出，但整体更为均衡，因此其更符合决策常识。由此可见，参数对比和参数值集成方法的应用中，突出参数会对缺陷参数形成中和，掩盖参数之间的极端失衡，最终导致非均衡决策方案的产生。

表8 F2的对象比较表

表9 各供应商模糊选择值

(二)水平软集决策方法

(三)相似度量方法

Alcantud提出了基于对象参数值计算得分值实现决策排序的策略[22]。该研究中同样没有涉及参数权重的讨论，在此将模糊软集F2各参数值与相应权重的乘积构建决策结果集，以应用该方法执行决策。最终得到各对象得分值如表10所示，从而有决策排序：s5>s3>s1>s6>s2>s4，供应商s5为决策选择。

表10 各供应商基于Alcantud方法的得分值

深入分析Alcantud的决策方法可以看出，该方法实质是基于对象各参数值与理想值相似程度的计算，因此是一种相似度量方法。纯定量方法确实具有较好的分辨性，但同时也伴随着方案的非均衡性，尽管Alcantud的方法较参数值集成方法有了一定改善。此外，计算复杂度较高也对该方法的应用形成了一定限制。

六、讨论与结论

伴随软集理论的不断丰富和发展，关于软集和模糊软集在决策中的应用研究也受到人们的持续关注，对其认识日益深入。

基于软集的决策，实质上是对参数化表达的对象所进行的选择，而参数之间的独立关系常常因决策中选择值的计算而被忽视；模糊软集是对参数的程度化描述，在其应用于决策的过程中，依然要基于参数的个体表现来判定整体性能。模糊软集中各对象参数对应的模糊数，表达了对该参数的隶属程度，虽然其取值大小也反映了对象在相应属性上的优劣状况，但囿于参数之间的独立性，很多学者对其可加性存有争议[14，22]。此外，仅基于数理有效性执行集成也易于导致非均衡决策方案的产生。

基于对经典软集决策所表现的简洁高效的深刻印象，模糊软集决策倾向于类推参数的定性判断策略。在这一策略的基础上，基于水平软集的决策方法的确具备了较高的操作简便性。然而，定性划分使得模糊参数传递的程度化信息转变为非好即坏的精确两级表达，而这必然带来分辨能力的局限[23]。同时，阈值的刚性则可能使相差无几的参数值分属优劣两组，于是丝毫差距导致了天壤之别。因此，单纯依靠阈值定性的方法与决策认知存在偏差。

有鉴于此，本文提出的模糊软集决策过程由两个阶段构成。首先，通过水平软集决策方法对论域对象进行粗分，以低度识别实现决策的总体均衡。其中，通过定义容差对水平软集的刚性阈值进行弹性调节，从而避免“毫厘之差以至天壤之别”的判断偏差。然后，对上阶段产生的备择集以相似度量方法予以精选。在水平软集的识别粒度下，以方案对理想解的相似状况执行排序，从而对整体决策的分辨能力予以完善。通过实例的验证并与现有典型模糊软集决策方法进行对比，本文提出的基于相似度量强化的容差水平软集决策方法展现了较好的适用性能。