基于虚拟仪器的汽车行驶跑偏测试系统误差校准研究
2018-10-15周灿
周 灿
(1.武汉理工大学 汽车工程学院,湖北 武汉 430070;2.武汉理工大学 现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070)
汽车行驶跑偏量是指待测车辆按照既定条件驶过跑偏测试区域后偏离理想直线行驶状态时的最大偏移量,不同汽车制造公司关于汽车行驶跑偏量的许用值不尽相同,但其大多数都不超过0.6 m/50 m。由于汽车四轮定位不准确、左右胎压不同、转向机构制造安装误差及形变等因素都可能会导致汽车生产下线时不可避免地产生一定的跑偏量[1],跑偏值过大不仅会加重车轮及其机械部件的磨损,而且会增加驾驶员驾驶时的疲劳强度,影响舒适性和安全性,因此汽车跑偏量测试是汽车道路试验中的一个重要测试项目,有必要在汽车出厂前进行汽车行驶跑偏量测试。
目前基于激光测距传感技术的跑偏检测设备已投入使用,其具有测试效率高、操作方便、工作过程稳定可靠等优点,为进一步提升汽车行驶跑偏量的检测精度,必须对不同的影响因素进行深入研究,尽可能地减少测试误差。
1 汽车跑偏测试系统概述
1.1 跑偏测试原理
基于激光测距的汽车行驶跑偏测试系统是以工业PC为主控制器,由激光测距仪测量与被测车辆距离,通过驱动程序驱动数据采集卡[2],实现数据采集、筛选、处理、测试结果显示和报表生成等功能,从而对行驶跑偏量定量定性分析的系统。试车员驾驶车辆进入测试区域时,可能因不规范操作引起较大的驶入角[3],对系统精度有较大影响,因此本测试系统引入3个测点,测试区域道路长度设置为50 m,其中测点一和测点二相距5 m,测点二和测点三相距45 m。在相应测点跑道两侧分别安装对射式光电开关,待测车辆进入测试区域后光电开关被车辆遮挡,信号由低电平变为高电平,触发激光测距传感器开始工作。
1.2 跑偏测试算法
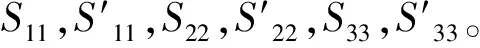
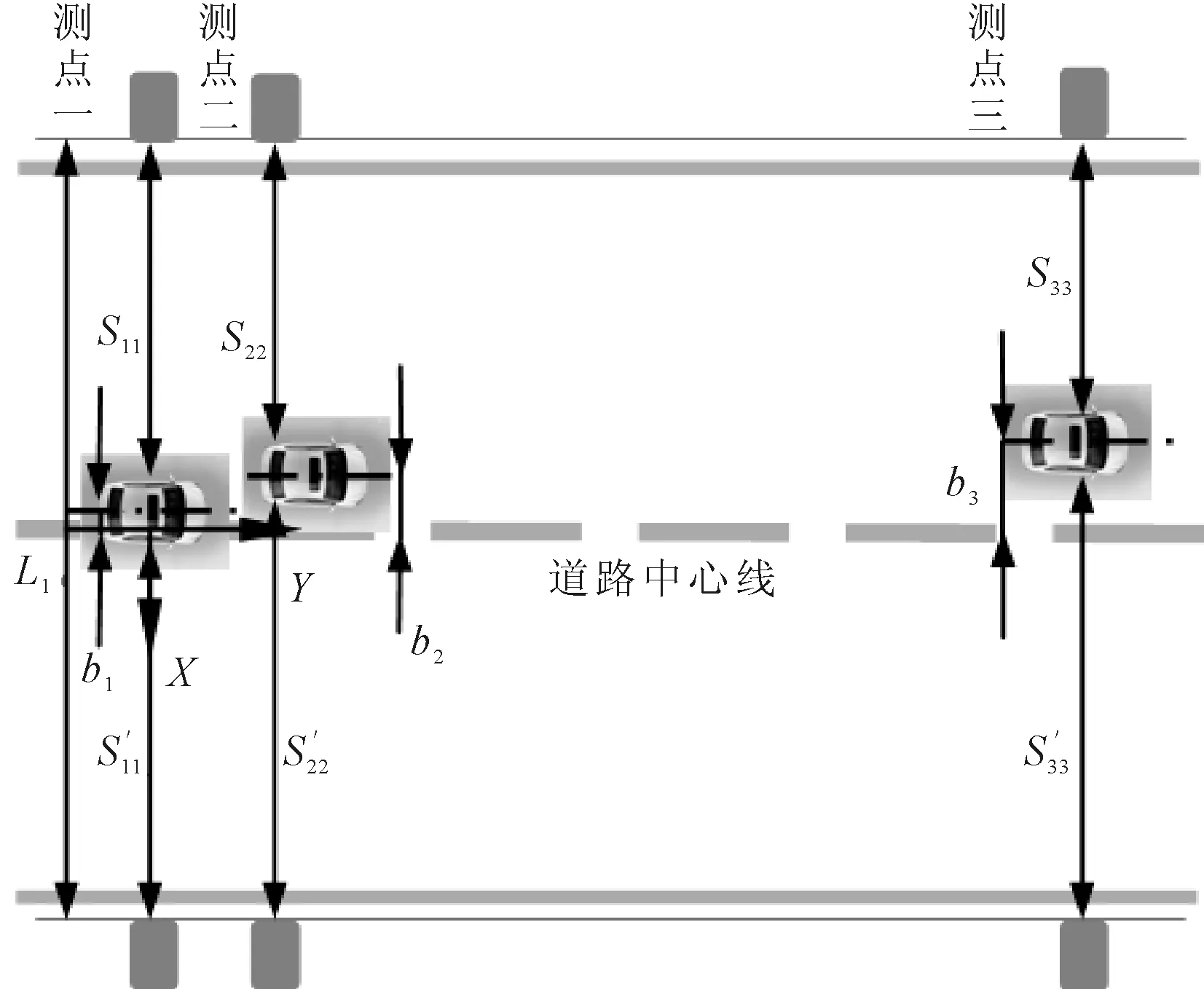
图1 车辆跑偏测试原理图
测点一左右两侧传感器之间的实际距离为:
(1)
测点一左右两侧传感器到道路中心线之间的距离为:
L11=S1+D/2
(2)
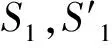
测点一左右相应的传感器到被测车辆纵向中心线的距离分别为:
(3)
则测点一处待测车辆纵向中心线距离道路中心线的距离为:
(4)
同理,测点二、三处待测车辆纵向中心线距离道路中心线的距离分别为:
(5)
式中:L21,L31,a2,a3的计算方法同式(2)和式(3)。
则测点一到测点三待测车辆纵向中心线的跑偏量为:
c=b3-b1=
(6)
当c>0时,车辆左偏;c<0时,车辆右偏。
测试过程可能由于操作不规范、硬件设备出现故障导致测试数据无效的情况,而跑偏量的处理结果最终由测点一和测点三测得的数据决定,因此可分为4组数据均无效,3组数据无效,两组数据无效,一组数据无效,所有数据均正常5种情况[5],具体分析结果如表1所示。
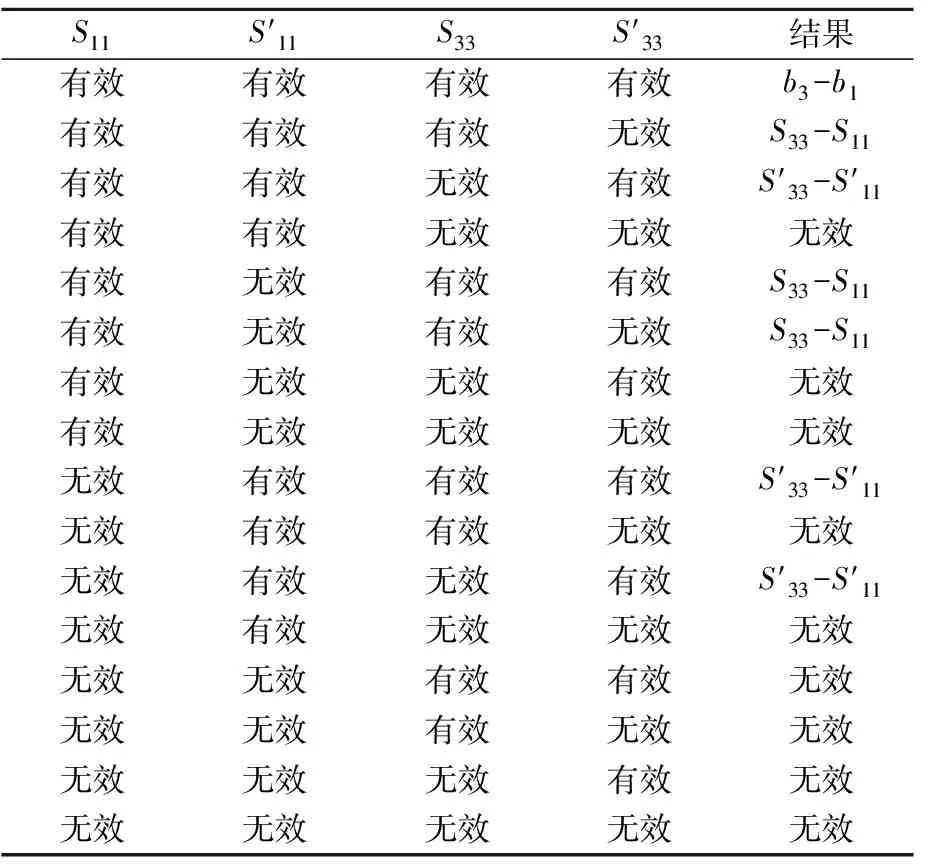
表1 跑偏量结果分析表
2 误差分析及校准
汽车行驶跑偏测试系统是基于虚拟仪器的自动测试系统,核心部件是属于NI公司的基于USB总线技术的C系列NI 9203 DAQ卡,具有高传输速率和200 kS/s的采样速率,但是测试过程不免产生意想不到的误差值[6],因此需要对该系统的误差构成具体深入分析并针对性校准补偿。测试系统的误差按性质分类可划分为随机误差、粗大误差和系统误差3种[7]。
2.1 随机误差及其处理
2.1.1 随机误差
以测点一为例,虚拟测试仪器在被测车辆车身部分采集的一组实测数据如图2所示。
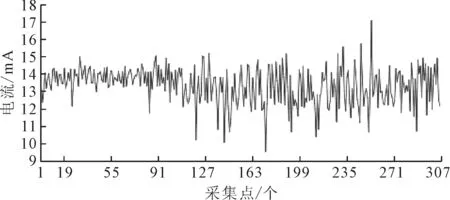
图2 电流实测数据图
在静态测量[8]以及激光测距系统等精度测量条件下,对待测车辆距测点处的距离S进行多次重复测量,得到的是不完全相同的测量结果,即每个测量值都有误差,经过大量数据分析并没有确定的规律来预测下一个误差的大小和方向,这就是测试系统产生的随机误差。随机误差是由很多暂时不能掌握或者不便掌握的微小因素构成,其产生原因主要包括以下几个方面:
(1)测量装置。测试系统安装箱内零部件间的配合不稳定性、调节机构长时间使用后的变形、激光测距传感器自身性能不稳定等。
(2)环境因素。温度的变化、光照强度的波动、路面水平度以及灰尘对电流采集板卡的影响等。
(3)人为因素。驶入过程方向的不稳定、标定瞄准读数时的不稳定性等。
2.1.2 随机误差的处理
从图2可知,在较大的数据采集量的情况下,测量值围绕着13.5 mA上下波动,在一定程度上反映了测量误差具有对称性、有界性和抵偿性的特征。由概率论和数理统计可知,随机误差就总体而言具有一定的统计规律,即服从正态分布[9]。
(7)
式中:μ为测量值的平均值,决定正态曲线的中心位置;σ为标准差,表征等精度测量值随机误差的离散程度,σ越小,正态分布概率密度曲线越陡峭,函数分布越集中,即大部分测量值都处于均值μ的两侧。
δi=li-l0
(8)
式中:δi为第i次测量的误差;li为第i次测量值;l0为真值;n为测量次数。
测点距待测车辆的真实距离在实际测量中是不可知的,即每次测量的误差也不可知,但跑偏量测试测量次数n远大于10,用算术平均值代替真值,用残余误差vi代替真值误差δi,再由Bessel公式得无偏估计:
(9)
即便是有限次测量,随机误差的算术平均值是一个有限小的量,当测量次数足够多,随机误差的算术平均值趋于零,对测试结果的影响就可予于忽略。因此在汽车行驶跑偏测试系统中,针对随机误差,其处理方法是在LabVIEW中设计程序时求有效数据的平均值。
2.2 粗大误差及其处理
2.2.1 粗大误差
由于汽车固有的表面形状特性,激光测距仪初始采集到的是车头部分的数据,曲率变化较大,两侧激光光束微小的不同轴都会造成光斑落点的不对称,采集到的数据相应的会有较大异常。采集车尾时也有同样的问题。因此在程序设计时,为保证采集到的数据为有效数据,首先应筛选出车身中部的数据作为初始处理对象。按照待测车辆在测试区的行驶速度为50 km/h计算,假设整车长度为4 m,则车辆通过任意测点大约用时0.16 s,而激光测距传感器的工作频率为1 kHz,即整车通过时采集的数据点有160个。车头、车身、车尾平均每部分采集53个点,然后通过程序来定位出车身中部的50个数据点作为运算基数。
2.2.2 粗大误差的处理
由积分概率表可知:
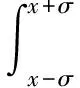
传感器测得的距离值x落在区间[x-σ,x+σ]之间的概率为68.3%;扩大到[x-2σ,x+2σ],概率为95.4%;扩大到[x-3σ,x+3σ],概率则为99.7%。即残余误差vi落在±3σ之外的概率仅有0.003,可以认为几乎是不可能发生的。由莱伊达准则,对任意的残余误差,其绝对值超过3σ,则视为粗大误差。因而在上述初步提取数据之后,要对满足莱伊达准则的数据进行再次剔除,重新计算σ的值,并与剔除后的数据再次进行比较,重复该过程,直至剩下的测量值误差中不存在粗大误差为止,以保证进入下一步程序处理的数据精度。该过程比较繁琐,但基于虚拟仪器技术,借助LabVIEW软件开发平台的实时处理,方便快捷的优势,可设计出满足条件的数据处理子程序。经过程序处理后,得到如图3的电流数据图。从图3可以看出,与初始实测数据图相比,处理后的电流波动小,更稳定,测量结果也更精确。
2.3 系统误差及其处理
2.3.1 系统误差
在车辆跑偏测试系统中,系统误差存在于信号采集和处理的各个环节:激光测距传感器的非线性和灵敏度误差、信号调理电路中的运放误差和滤波误差、DAQ数据采集卡的采样误差、A/D转换误差、光纤传递误差、计算机处理误差等。汽车跑偏测试系统的误差传递过程如图4所示。系统误差的特征则是在同一条件下,对同一个测量值,误差的符号和绝对值不变,或者在条件有变化时,误差按照一定的规律改变。因此系统误差不具有补偿性,即便是多次测量求平均值,也不能减少它的影响。根据系统误差的特点:服从某一规律,不易被发现,但是通过分析误差源,可以通过系统校准的方式减少其影响。

图4 误差传递过程
由图4可知,在跑偏测试系统中,被测信号进入虚拟测试仪器后,经过一系列变换后才转变成输出信号,这个过程主要包含了两个方面:系统传递函数转换的误差和虚拟测试仪器本身的误差。误差传递过程的几个环节是串联的,假设各环节误差传递系数分别为
η
1
,
η
2
,
η
3
,
η
4
,
η
5
,那么整个系统的误差传递函数
η
则为:
η=η1·η2·η3·η4·η5
输出信号的误差Δ则为:
Δ=(1+φ)·η·ψ
式中:φ为传感器采集到的距离信号进入系统时自身带有的误差;ψ为跑偏量测试系统仪器本身误差。
2.3.2 系统误差的处理
在测试系统整体固定安装完成后,这些误差不可能在内部一一处理,因此,由系统误差固有的规律性,以及其主要通过误差传递函数的形式出现,结合虚拟仪器“软件即仪器”的固有特点,可在标定时采取一系列校准测试获得一个总的误差传递函数,对系统进行修正,从而提高系统的测试精度。误差校准示意图如图5所示。
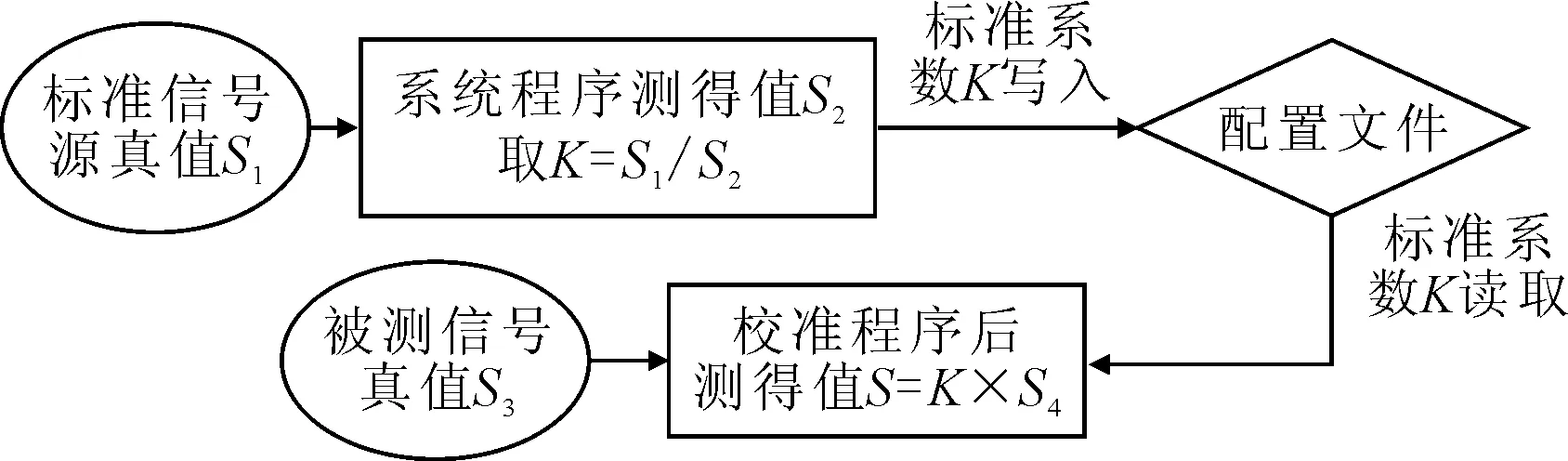
图5 误差校准示意图
基于以上原理,提出了对车辆跑偏测试系统测试结果校准的办法:
(1)采用标准信号源S1[10]作为系统校正的基准,在该系统中,将激光测距传感器在现场直接读得的数据计算出的跑偏量定为标准跑偏量S1;
(2)在LabVIEW软件开发平台设计一个校准程序,如图6所示,该程序与跑偏测试系统一致,并用该程序对标准源S1进行测量,在PC端得到跑偏量S2,校准系数K=S1/S2;
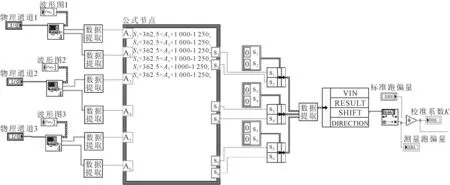
图6 生成校准系数程序图
(3)LabVIEW程序中有生成文件模块、写文件模块,调用这些模块并用数据流连接,即可将校准系数K写入LabVIEW的一个标准配置文件中,如图7所示;
(4)在校准程序中设计读取配置文件部分,并嵌入到测试系统中,测试信号真值为S3,如图8所示。测试系统正式运行时,先从配置文件中读取校准系数K再测量,计算机端先得数据S4,再使用K进行校准,最终输出测试结果,校准后的跑偏量S=K×S4。
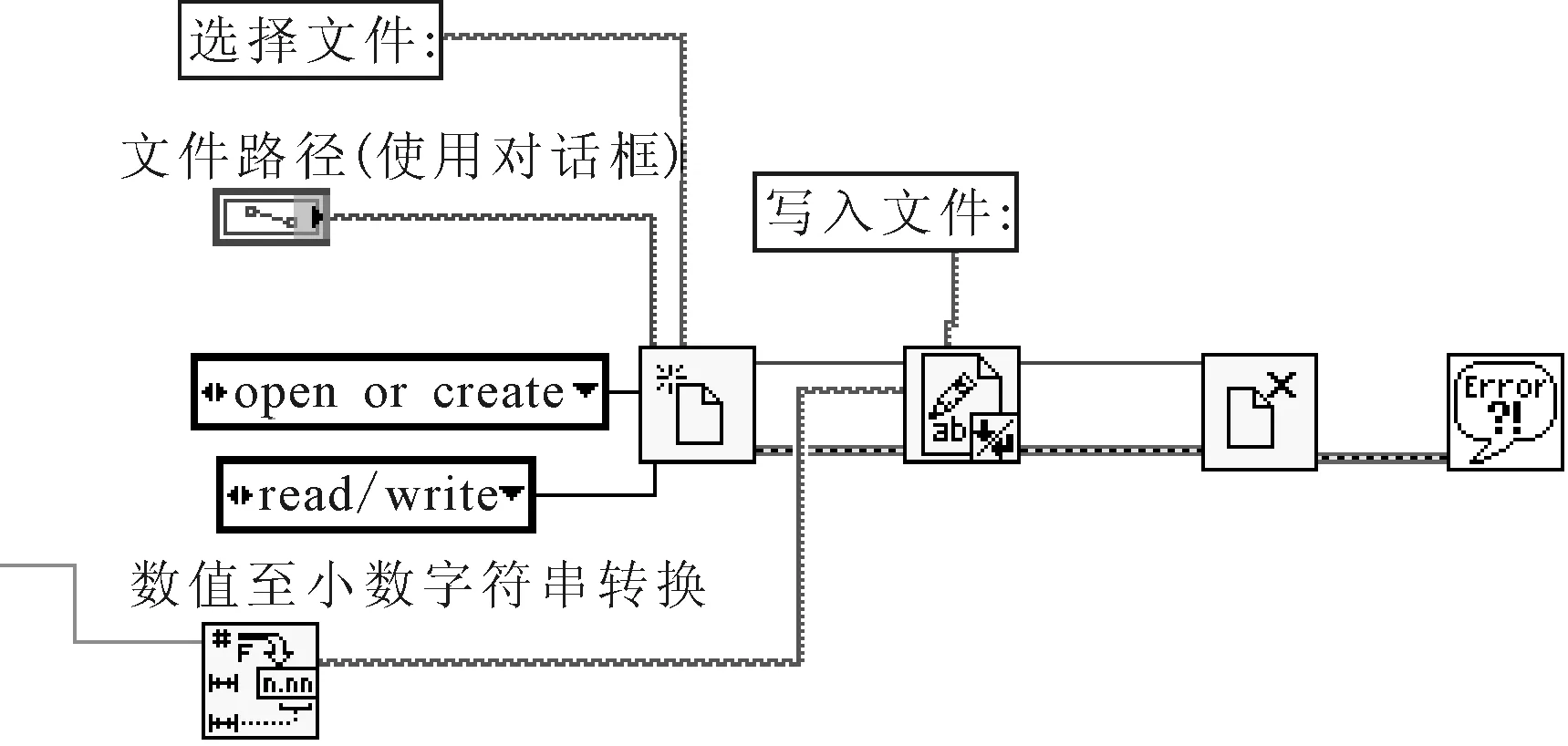
图7 写入校准系数程序图
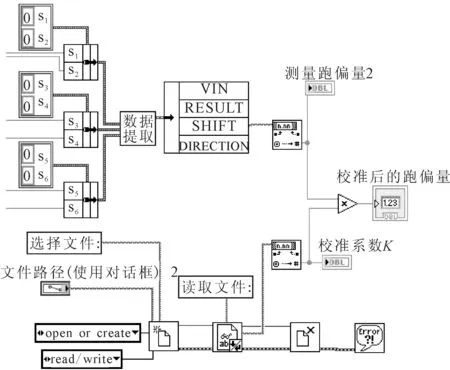
图8 读取配置文件程序框图
部分测试结果如表2所示。
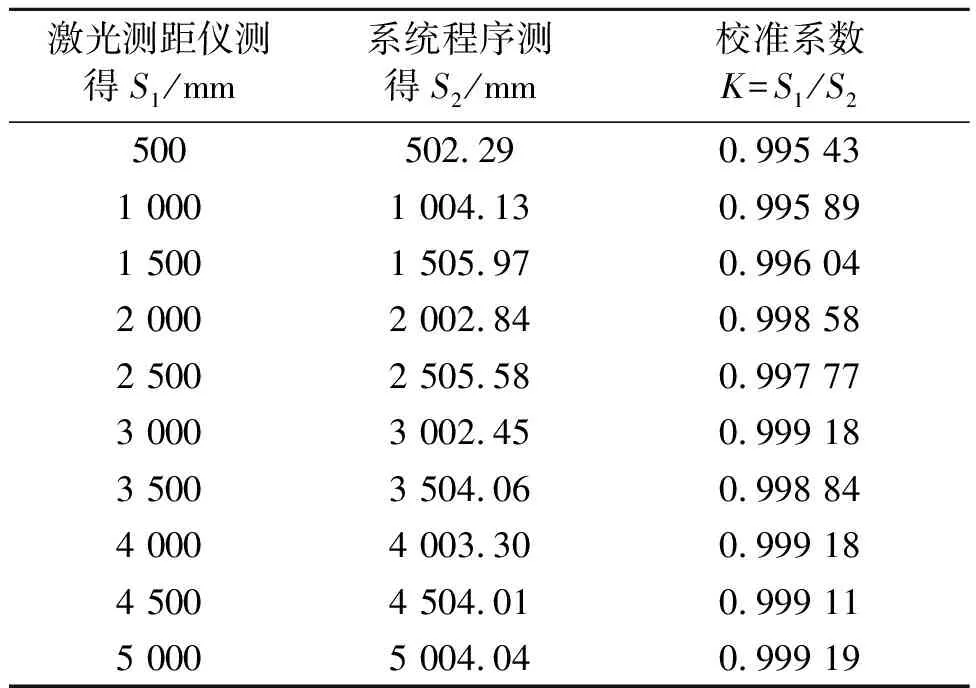
表2 部分测试结果
为保证系统的准确性和可靠性,取K的平均值为该项目的校准系数,得K=0.997 92。
3 测试试验
以新下线车辆为被测目标,试车员驾驶车辆沿着道路中心线以50 km/h稳速行驶。该系统使用高精度的激光测距仪(测量范围为200~6 000 mm)作为理想源,测距仪在现场直接测量后通过跑偏测试算法计算跑偏量,将其作为真值S3;在校准前通过测试系统主程序得测试结果S4;调用校准系数K后计算最终的跑偏量为S。分别计算在误差校准前和校准后二者的相对误差和,部分试验结果如表3所示。
从表3可知,被测车辆跑偏量大体在30 cm内,即待测车辆符合跑偏量的规定要求。比较校准前与校准后程序所得结果易知,在误差校准之前,车辆跑偏量测量系统的相对误差在1%左右[11],而在进行了误差校准后该系统精度大幅提高,将误差缩小了约0.2%,并且该程序的开发可以达到模块化的要求,容易集成,为系统升级也提供了便利,性能更高,可靠性更强。
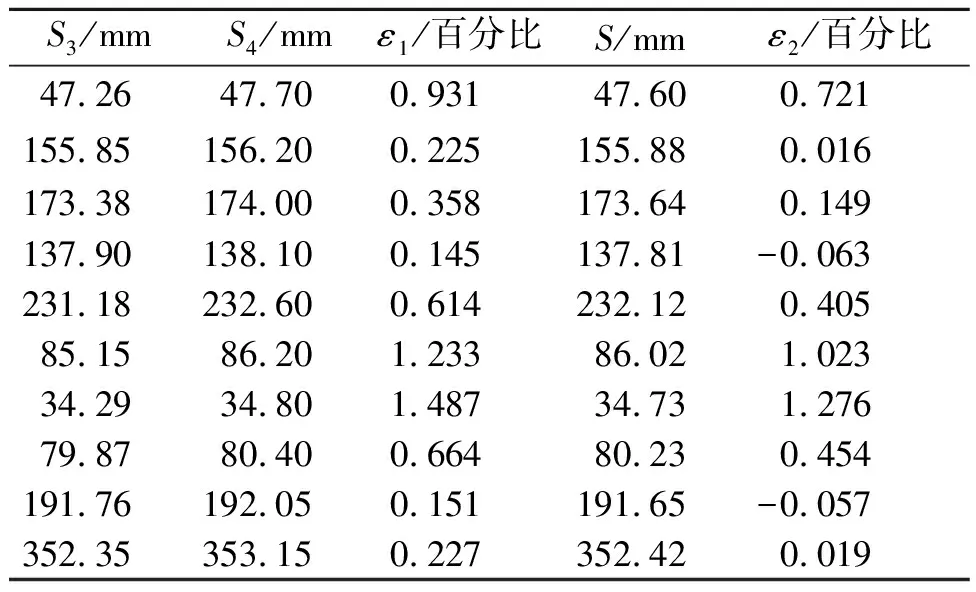
表3 部分试验结果
4 结论
(1)汽车跑偏量测试时数据量巨大,计算过程繁琐,通过在LabVIEW软件开发平台上对测试程序的合理设计,可以对系统产生的数据进行快捷、实时的处理,并对汽车行驶跑偏量进行定量定性的分析。
(2)结合试验数据分析了正态分布下的随机误差具有对称性、有界性、抵偿性的特征,用求算术平均值的办法抵偿误差;并通过对车身数据采集点的位置分析,利用Bessel公式和莱伊达准则对粗大误差进行剔除,保证了运算数据的稳定性和精确性。
(3)针对汽车行驶跑偏测试系统,分析系统误差的传递原理,提出的误差校准办法具有较高的实用性,可以显著减少误差对所设计系统测量结果的影响,使测试系统精度大幅提高,符合测试技术指标要求。
