基于SDAE-SVM的压力机轴承故障诊断方法

张庆磊，张 枫

(武汉理工大学 机电工程学院,湖北 武汉 430070)

由于压力机高强度、高频率的作业特点，会造成压力机的轴承内环、外环和滚子产生点蚀、裂纹和表面剥落等缺陷[1]。在压力机发生故障时，约有30%是轴承故障，并且出现轴承故障不易及时发现与维修，将会导致生产效率下降，甚至会导致严重的安全事故。因此利用有效的故障诊断方法，监控压力机轴承的运行状态，可以合理安排维修时间，大大降低维修成本，提高生产效率。

近年来，深度学习受到广泛关注，尤其在故障诊断方面得到广泛的应用[2]。Tran等把DBN(deep neural network)和TKEO(Teager-Kaiser energy operation)算法融合[3]，应用到往复式压缩机阀门故障诊断中。Li等[4]提出一种多模式分类的方法，并应用到齿轮的故障诊断中去，有效提高了齿轮故障诊断的准确率，并解决了单一振动源下诊断精度不高的问题。Jia等[5]把深度神经网络应用到轴承的故障特征提取和诊断中，其利用深度神经网络的特征提取能力，直接从频域信号进行轴承故障特征提取和识别，取得了较好的效果。Lu等[6]研究了深度神经网络在旋转轴承频域信号中的故障特征提取能力，并给出了故障特征的可视化结果。

笔者针对传统机器学习存在的问题以及压力机轴承的故障特点[7-10]，基于去噪自编码器和支持向量机，提出了一种基于SDAE-SVM(stacked denoising auto encoder networks-support vector machine)的压力机轴承的故障诊断方法。相较于传统的机器学习，该方法集成了特征提取和状态分类两大步骤[11]，该方法建立深层网络模型，利用逐层贪婪训练的方法实现对高维深层故障特征的自适应挖掘，能够显著提升故障识别能力和泛化能力。首先基于堆叠去噪自编码网络(SDAE)和SVM建立故障诊断网络模型，其次通过选取样本数据，PCA(principal component analysis)降维并归一化处理，划分训练集合测试集，再次预训练网络模型，然后通过BP(back propagation)算法微调优化网络参数，最后通过测试集数据测试网络模型的诊断性能。实验结果显示该方法能有效提高压力机轴承的故障诊断准确率。

1 堆叠去噪自编码网络模型

堆叠去噪自编码网络(SDAE)是深度自编码网络的一个变种，它是用去噪自编码器(DAE)来替代自动编码器(SAE)，通过多层DAE栈式堆叠，从而建立堆叠去噪自编码网络(SDAE)，实现对高维特征的提取。从结构上看，堆叠去噪自编码网络是由多层无监督的去噪自编码器(DAE)和一层BP神经网络组成，其网络模型结构如图1所示。

图1 SDAE网络模型

SDAE的核心思想是通过对每层编码器的输入加入噪声来进行训练，从而学习到更强健的特征表达。通过去噪自编码训练得到的SDAE网络不仅学习到原始数据的特征，还能学习到被“破坏”后的退化特征具有更强的泛化性、鲁棒性。SDAE的训练过程分为预训练和微调两个阶段。

1.1 预训练

去噪自编码器结构由编码器(encoder)、解码器(decoder)和隐含层组成。SDAE预训练的过程实质上就是初始化网络参数的过程，其主要采用逐层无监督特征优化算法[12]进行。去噪自编码原理[13]如图2所示。

图2 去噪自编码器原理图

去噪自编码器首先将原始输入x添加一个随机噪声，得到一个含有噪声的x1。

x1～qD(x1|x)

(1)

式中：D为数据集；q为随机噪声。

此时编码器的输入是原始数据被破坏后得到的x1，通过编码器函数fθ(·)映射到隐含层，可表示为：

y=fθ(x)=s(Wx+b)

(2)

式中：s为映射函数；W为权重；b为偏置；θ为集合参数。

经过编码后的y会通过解码器函数进行信号重构过程：

z=gθ′(y)=S′(W′y+b′)

(3)

式中：S′为映射函数；W′为权重；b′为偏置；θ′为集合参数。

这样对于每一个输入xi都被映射到一个yi，然后得到重构函数zi，再通过不断优化模型所有的参数，最小化输入和重构解码的误差可得：

L(xi,zi)=‖xi-zi‖2

(4)

(5)

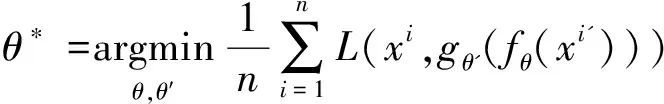
(6)

1.2 微调

完成SDAE网络预训练后，所得的SDAE网络的权重以及分类层权重作为深度网络的初始参数，这些参数看作接近全局最优的网络参数，然后对SDAE网络参数进行微调。微调过程是有监督学习过程，即通过采用标签数据进行训练，利用反向传播BP算法对网络参数进行微调，应用梯度下降算法进行权值的更新，最终使网络达到全局最优。

首先定义输出层lnl的单元i的残差为：

(7)

然后定义隐藏层l=nl-1,nl-2,…，2的残差表达式为：

(8)

式中：i为隐藏层l的第i个单元；j为隐藏层l+1的第j个单元；1≤j≤sl；ρj为第j个单元的平均激活值。

损失函数对W，b取偏导数可得：

(9)

式中：C(W,b;x,y)为输入和输出的均方误差函数。

最后最小化目标函数进行参数更新：

(10)

式中：η为参数更新时的学习率。

2 SVM分类器

SVM分类器是基于统计学的机器学习方法，SVM的核心思想是最大化分类间隔，是一种融合统计学与核函数的分类器。SVM对输入数据采取非线性映射，将其映射到高维特征空间。

假定大小为n的训练样本集{(xi,yi),i=1,2,…,n}由两类别组成，其中xi为类属性，yi为类标记，n为样本集个数，SVM分类器将低维空间的输入映射到高维空间，以此寻找最优超平面，其超平面定义如式(11)所示。

(11)

式中：ai为拉格朗日乘子；K(x,xi)为核函数；b为偏置。

本文的SVM分类器选用高斯径向核函数：

(12)

(13)

当惩罚参数越大时，越不能容忍误差；惩罚参数越小时，越欠拟合。当核函数参数越大，支持向量越少，核函数参数越小，支持向量越多。

通过SDAE建立的诊断模型可以满足一定程度的故障诊断需求，但在对诊断要求较高、故障模式复杂情况下，通过在SDAE最后一层加入SVM分类器，利用支持向量机通过最大化分类间隔的特点来实现分类识别，可以有效提高分类的准确性，并且提高网络的鲁棒性和泛化能力。

3 基于SDAE-SVM故障诊断方法实现

3.1 模型建立

笔者基于SDAE自适应特征提取的特点以及SVM处理多分类问题的优点，构建了SDAE-SVM网络模型，它的前部是由堆叠自编码网络(SDAE)构成，最后一层增加了代表期望输出变量的分类层，即SVM分类器。其网络模型如图3所示。该模型通过采用SVM分类器优化SDAE网络，通过最大化分类间隔来实现模式判别，能够有效提高网络模型的鲁棒性和分类识别性能。它在给出分类结果时还会给出结果的概率，适用于非线性多分类问题。

图3 SDAE-SVM网络结构模型

基于SDAE-SVM的压力机故障诊断方法具体实现步骤如下：

(1)基于SDAE与SVM建立SDAE-SVM网络模型，并将模型的参数初始化为随机较小数值。

(2)选取样本数据和特征变量，对样本数据进行PCA降维后归一化处理，然后按一定比例将其分为训练集和测试集。

(3)对压力机轴承故障状态类型进行编码。

(4)采用训练集中的无标签数据通过BP算法对模型底部SDAE层逐层预训练。

(5)采用有标签的数据样本通过BP算法对整个网络模型进行调优，微调网络参数，使得网络性能趋近全局最优。

(6)保存训练好的网络，并利用测试集中的数据样本对网络模型的诊断性能进行测试。

具体的故障诊断流程如图4所示。

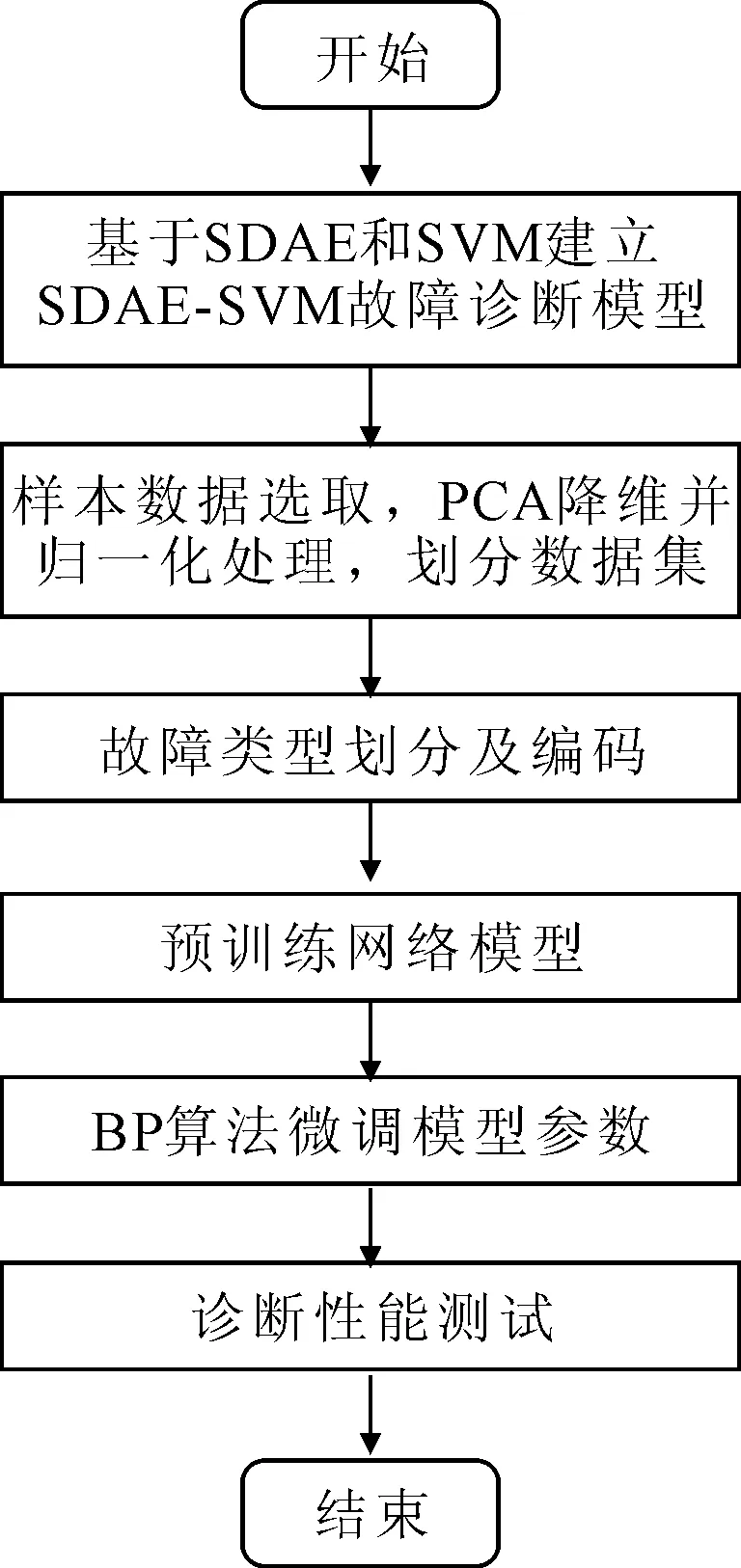
图4 基于SDAE-SVM的压力机轴承故障诊断流程图

3.2 样本选取

通过压力机在线状态监测系统采集压力机轴承相关数据，选定飞轮轴承的故障数据作为实例分析的数据样本。本次实验选定某段时间在线状态监测系统采集的飞轮轴承数据，采样长度为2 000，共有3 000个样本。轴承的故障类型如表1所示。

表1 故障类型

3.3 故障类型状态编码

轴承故障诊断是一个多分类任务，诊断结果可以分为正常状态、内圈轻度故障、内圈中度故障、内圈重度故障、外圈轻度故障、外圈中度故障、外圈重度故障、滚动体轻度故障、滚动体中度故障、滚动体重度故障10种类型，对于轴承的故障诊断实际上就是对故障类型的状态码进行识别分类的过程[14]，下面依次对其进行编码，如表2所示。

表2 轴承故障状态编码

4 实验结果分析

4.1 网络层数对模型性能的影响

SDAE-SVM不同于传统浅层结构，这种网络结构深度通常大于2层，为了对比不同网络层数对整体分类性能的影响，将网络层数分别设置为3～8层进行对比，其中输入层样本维数为400，输出层分类类别为10，网络结构为[400-200-100-10]，每个隐含层的节点数设置为100，学习率为0.2，噪声系数为0.2，迭代次数为400；将网络层数从3变化至8，分类准确率如表3所示，其误差收敛曲线如图5所示。

表3 不同网络层数的SDAE-SVM实验结果

图5 不同网络层数收敛曲线图

从表3可知，SDAE-SVM模型随着网络层数的增加其识别准确率先呈现递增后递减的趋势，这是由于随着去噪编码层的增加，可以提高网络模型的学习性能，高层学习到的特征是输入的多级抽象表达更接近输入的特征，进而提高分类性能，当网络层数为4层时，网络的学习性能最佳，识别准确率高达98.08%。然而随着网络层数的增加会导致网络模型的复杂度提高，会给网络带来更多的参数，从而导致网络不稳定，泛化性能大大降低，容易出现过拟合现象，使网络的分类性能持续下降。

4.2 Batchsize值对模型性能的影响

针对不同Batchsize值对模型性能的影响，本次实验选择网络结构为[400-200-100-10]，迭代次数为200，学习率为0.2，噪声系数为0.2，采样长度为2 000，共有3 000个样本，训练样本占总样本的90%，共有2 700=22×52×32个样本，因此Batchsize选择2、4、6、10、20、30、60、100，模型的分类准确率如表4所示。不同Batchsize值的误差收敛曲线如图6所示。

表4 不同Batchsize值的SDAE-SVM实验结果

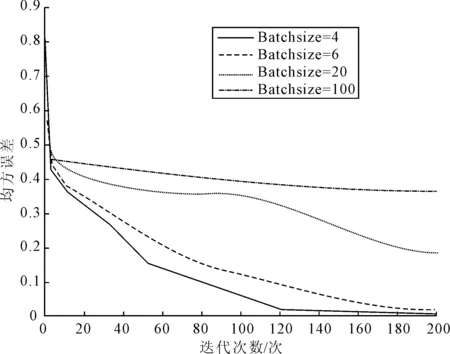
图6 不同Batchsize值的误差收敛曲线图

由表4可以看出，随着Batchsize值的增大，网络的分类准确率先递增后递减，并且当Batchsize值为4时，网络的分类准确率高达98.08%，由图6可以看出，当Batchsize过大时，网络收敛困难，精度降低从而导致分类准确率下降，综合考虑识别率来看，Batchsize值为4时网络的分类性能最优。

4.3 与SDAE、SVM方法的对比分析

根据实验结果，可以确定网络层数为4，Batchsize值为4时分类性能最优。为验证本文方法相较于SDAE和SVM的分类性能更优，将分类结果与SVM以及SDAE网络进行了对比。SVM选择高斯径向核函数，SDAE采用与SDAE-SVM相同的网络结构，其拓扑为400-200-100-10。实验结果如表5所示。

表5 3种方法的分类结果对比

由表5可知，通过SVM分类器优化所得到的SDAE-SVM网络分类性能显著提升，深入分析可知，SDAE方法分类能力强于SVM的原因是其深层非线性网络将原始数据一层一层抽象，自适应提取特征更能描述对象本质且易于分类。而SDAE-SVM网络通过结合SVM分类器优化网络最后一层，大大提高了网络的鲁棒性和泛化能力，从而提升了网络的分类识别性能。

图7为采用SDAE-SVM方法进行故障分类识别的混淆矩阵，可以看出第1， 3，7，9，10种故障状态的识别率均为100%，总体的故障识别准确率也高达98.08%，由此可以说明基于SDAE-SVM的故障诊断方法能有效提高压力机轴承的故障识别精度。

图7 SDAE-SVM分类混淆矩阵

5 结论

笔者结合SDAE自适应特征提取的特点和SVM处理多分类问题的优点，提出了一种基于SDAE-SVM模型的压力机轴承故障诊断方法，在针对压力机在线状态监测数据的故障识别实验过程中，SDAE-SVM模型具有良好的故障识别性能，实验分析了网络层数，Batchsize值大小对于网络性能的影响，并且对比分析了SDAE、SVM方法的分类性能。实验表明SDAE-SVM模型对压力机轴承的故障识别率高达98.08%，具有良好的故障识别精度，因此验证了该方法应用于压力机轴承的故障诊断中的可行性。