复合控制导弹反步滑模IGC自适应设计方法
2018-10-15董朝阳程昊宇
夏 川, 董朝阳, 王 青, 程昊宇
(1. 北京航空航天大学航空科学与工程学院, 北京 100191; 2. 北京航空航天大学自动化科学与电气工程学院, 北京 100191; 3. 西北工业大学航天学院, 陕西 西安 710072)
0 引 言
传统的导弹制导与控制系统分别设计制导回路和控制回路,在此框架下,需要反复设计两个回路,无法达到最优性能,且未考虑两个回路间的耦合,全局稳定性不能在数学上得到严格证明[1]。制导与控制一体化(integrated guidance and control, IGC)[2-3]方法根据弹目相对运动状态直接产生控制指令,能够提高导弹机动能力、作战响应速度及攻击精度。
国内外已有学者对此进行了许多有意义的研究,文献[4]选取合适的二次加权函数将制导与控制问题转化为仿射动态约束下的离散时间有限时域二次优化问题。文献[5]基于反步滑模控制设计模糊逼近器,对内外不确定性进行补偿,但由控制器直接求解出的控制量较大,响应剧烈。文献[6]将一类高速旋转导弹线性化为一个线性参数时变(linear parameter-varying,LPV)系统,并设计IGC算法,消除了旋转引起的横向耦合。文献[7]针对一类舵机具有开关特性的导弹,设计滑模控制器,实现了对不精确建模和目标机动的误差抑制。文献[8]建立了高超声速飞行器再入段IGC严反馈模型,通过自适应动态面将10阶非线性不确定系统的控制器设计问题转化为输出调节问题,证明了系统一致最终有界。
现代战争中目标机动性越来越高,入侵空天领域越来越大,例如对临近空间高机动性目标进行拦截和打击时,空气稀薄,气动舵面甚至失效。直接力/气动力复合控制技术可有效解决这一问题,提高导弹动态性能。然而,横侧向喷流与空气流场发生的复杂干扰效应将会出现于脉冲发动机作动时,导弹飞行气动区域内会出现分离激波和分离涡等复杂的气动现象[9],对控制系统的抗干扰设计提出了更高的要求。文献[10]基于扩张状态观测器(extended state observer,ESO)为反射镜稳定平台设计了一类自适应鲁棒控制器,对模型误差和外界干扰力矩具有鲁棒性。文献[11]设计了一类具有误差补偿的线性ESO,但自适应滑模控制器的参数切换会引起观测器输出小幅抖动现象。文献[12]提出一种模糊逼近方法,用以逼近未知不确定性,但需假设状态的范围,模糊基函数选取较为随意。文献[13]为吸气式高超声速飞行器设计了非线性误差观测器,保证了在输入限幅、气动参数不确定情况下的误差观测效果。
针对直接力/气动力复合导弹,在发动机约束、舵偏约束等多约束条件下,如何发挥多执行机构优势,使得控制达到最优是需要解决的问题。控制分配是解决这类问题的有效方法[14-16]。传统方法先设计气动控制回路,再进行直接力分配设计,这样两步分开的做法避免了控制系统综合设计的困难,但设计经验性很强,且需要反复设计才能获得较好的控制策略[17]。文献[18]在执行机构不对称性和饱和约束情况下,基于凸优化和非线性规划,设计回归神经网络控制分配器,但通过实验获取分配器,缺乏理论依据效率较低。文献[19]提出一种修正的广义逆矩阵方法,将控制分配问题抽象为约束条件下的参数化输入矩阵归零问题,但推导复杂,难以运用于工程实践。
本文在以上研究的基础上,使用ESO对气动参数摄动、喷流干扰、建模误差等复合干扰进行观测,并设计自适应律对观测误差进行补偿;使用反步法设计滑模控制器,通过自适应补偿来抑制复合干扰对系统的影响;随后定义了一个虚拟控制力矩,规避了在控制器中直接求解控制量,并基于梯度下降法和混合整数线性规划提出一种自适应控制分配策略,充分使用了控制系统中误差信息,在误差增长快时能够提高解算的实时性和精度,使系统快速收敛,误差不再增长。最后仿真验证了IGC控制器设计方法、控制分配策略的有效性。
1 IGC系统建模
以导弹俯仰通道为例来说明直接力/气动力复合控制导弹的IGC问题,偏航、滚转通道可以通过设计协调通道与俯仰通道解耦[20-21],在此不再赘述。
1.1 弹目相对运动模型
弹目相对运动关系如图1所示,XOY为惯性系,M和T分别代表导弹和目标,R为弹目相对距离,λ为视线角,VM、VT分别为导弹和目标速度,θM、θT分别为导弹和目标的弹道倾角。
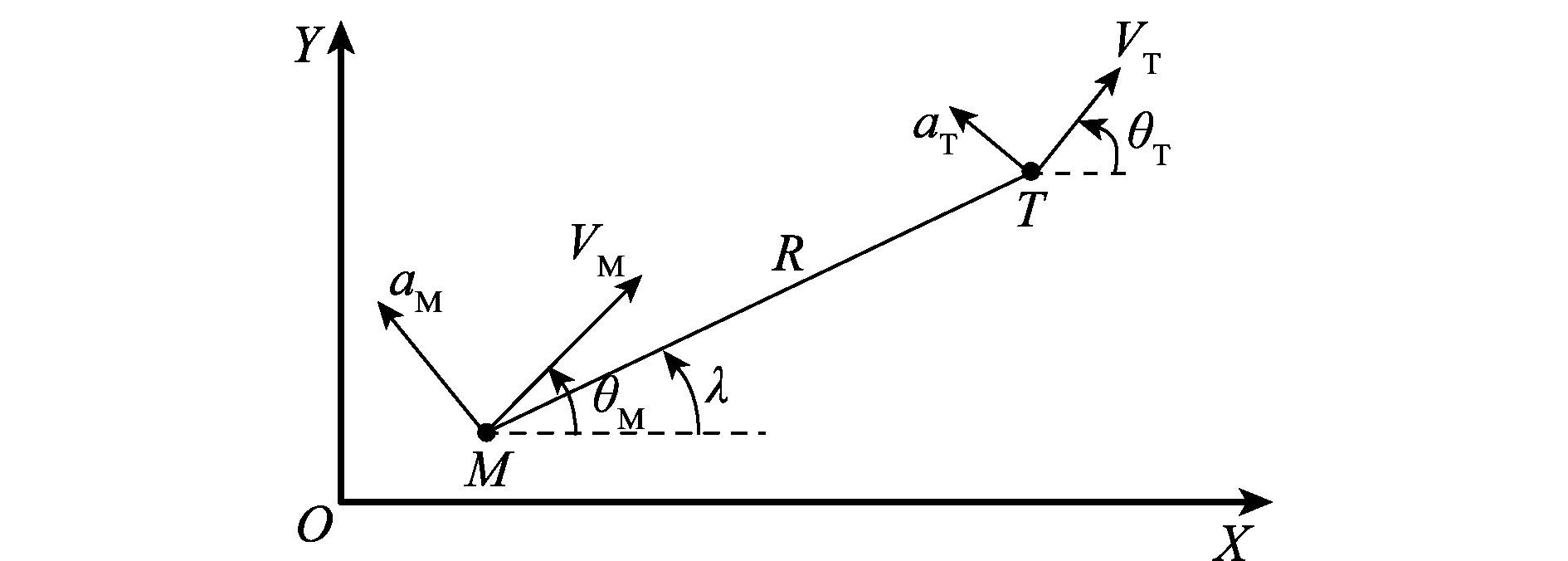
图1 弹目相对运动关系图Fig.1 Missile and target relative motion geometry
由图1可得导弹和目标在纵向平面的相对运动方程为
(1)
(2)
对式(2)求导可得
(3)
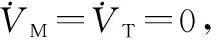
(4)
控制系统的设计目标是使相对速度Vr→0,相对距离R→0。
1.2 直接力模型
当气动舵效率不足时,为提高导弹动态响应,使用脉冲发动机产生侧向力和力矩,如图2所示,脉冲发动机共有10环,每环18个,相邻的两环间隔10°交错排列,令e为圈号,e=1,2,…,10,p为脉冲发动机在各自圈内的编号。
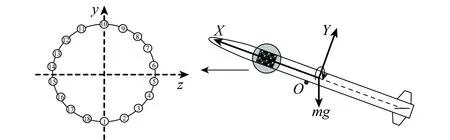
图2 脉冲发动机示意图Fig.2 Diagram of pulse engine
弹体坐标系下不同位置的脉冲发动机产生的力矩[22]为
式中,当e为奇数时,e*=2;当e为偶数时,e*=1。
脉冲发动机一般成对使用,当导弹载重有限时,仅使用位于z轴和y轴上的4个脉冲发动机就能产生所需要的控制力矩。本文在纵向平面内仅使用位于正y轴方向5个和负y轴方向5个共10个脉冲发动机。脉冲发动机安装紧凑,忽略不同脉冲发动机与质心的间距差别。
已知单个脉冲发动机的推力F随时间的变化规律可近似为
(5)
式中,Fm为稳态推力;τ为推力延迟时间;由于τ值较小,发动机较快达到稳态喷流,关闭发动机时推力迅速衰减,通过近似将脉冲发动机特性描述为矩形脉冲,总的直接力Fc可表示为
Fc=nF
(6)
式中,n为一个喷流周期内,使用的脉冲发动机个数,0≤n≤5;上次喷流后不能马上再次使用标号相同的脉冲发动机,最小喷流间隔时间为t0。
1.3 IGC模型建立
纵向平面内导弹动力学模型[23]为
(7)
式中,m为导弹质量;α为攻角;ωz为俯仰角速度;ϑ为俯仰角;Jz为导弹对z轴的转动惯量;MZ为俯仰力矩,表示为
MZ=M0+Mδzδz+Mf
(8)
δz为升降舵偏角;Mδz为舵偏角力矩系数;Mf=LTFc为脉冲发动机产生的力矩;LT为脉冲发动机到导弹质心的距离,取平均值;M0=M0(α,M,h,Vt,ωz)为攻角,马赫数和高度等因素引起的力矩,通常线性化[24]为
M0=Mαα+Mωzωz
(9)
其余力和力矩可写为
δz)
(10)
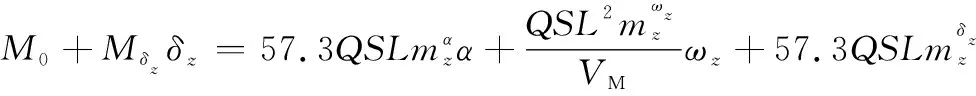
(11)
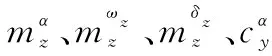
末制导段导弹速度近似为常值不变[5],假设有界复合干扰为dv、dα、dωz,复合干扰包括模型误差、脉冲喷流干扰及目标机动和气动参数不确定性等,推导得到IGC模型为
(12)
(13)
(14)
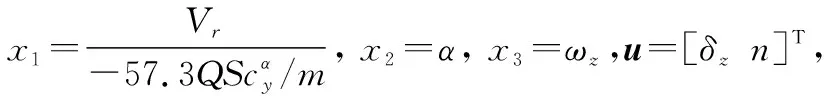
(15)
式中
|di|≤di,max,i=1,2,3
系统受到喷流干扰产生的附加未知干扰力和力矩的影响,并且气动参数存在摄动,目标存在机动。在复合干扰条件下,进一步设计控制器及控制分配策略。
2 制导控制律及控制分配策略设计
2.1 IGC控制器设计
设计控制律使式(15)表述的存在复合干扰的严格反馈非线性系统的状态变量x1收敛至零,利用反步法分3步进行IGC设计。
步骤1对式(15)中子系统1
(16)
进行外环设计,设计滑动模态面为
s1=x1
(17)
当系统在该滑模面滑动时,状态将快速下降,使得状态x1→0,将s1对时间t求导得
(18)
由于d1为系统内外干扰,无法预知,设计式(19)所示的二阶ESO对其进行观测[25]。
(19)
式中,β11,β12为观测器增益;函数fal(·)可以避免高频震荡,定义为
(20)
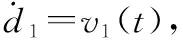
(21)
定义
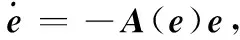
观测器的输出满足
Z11→x1,Z12→d1
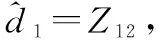
(22)
为消除逼近误差E12的影响,引入自适应律对观测误差进行补偿,以提高制导精度,减小脱靶量。定义x2为外环控制量,则虚拟控制指令x2c可写为
(23)
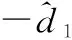
(24)
式中,c1>0,γ1>0,ρ1>0为待设计的参数。自适应律可以对系统误差进行补偿,减小系统控制误差。
为避免下一步设计中对虚拟控制量求导,避免反步法设计中存在的“计算膨胀”问题,设计一阶低通滤波器对虚拟控制量x2c进行滤波,即
(25)
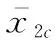
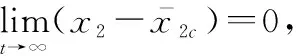
(26)
将式(26)求导可得
(27)
与步骤1类似,采用ESO对未知复合干扰d2进行观测
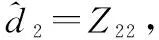
(28)
为补偿观测器的观测误差,将虚拟控制指令x3c写为
(29)
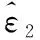
(30)
(31)
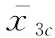
步骤3对式(15)中的子系统3进行内环设计,定义复合虚拟控制力矩为
v=bu
(32)
其与真实力矩的关系为
(33)
(34)
对时间t求导可得
(35)
同理,采用ESO对未知复合干扰d3进行观测,即
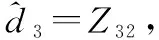
(36)
为补偿干扰观测误差,复合虚拟力矩v可以写为
(37)
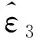
(38)
综上所述,给出完整的一体化控制律为
(39)
由式(39)可看出,通过引入复合虚拟控制力矩项,规避了直接在控制器中求解控制量,通过控制分配策略,即可求解出所需的舵偏量和使用的脉冲发动机个数。
2.2 自适应控制分配策略
定义整体精度为
χ=v-bu
(40)
v为虚拟控制力矩,b∈R1×2为控制效率矩阵,u∈R2×1为控制量。操纵面偏转位置和偏转速率满足
(41)
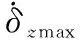
假设计算机离散系统控制周期为T,操纵面偏转的位置约束集合为凸集,表示为
(42)
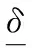
(43)
脉冲发动机的使用约束集合为
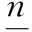
(44)
s.t.δ∈Ωδ,n∈Ωn
式中,Wn和Wδz为脉冲发动机和舵机使用惩罚权重,均为正常值,为适应分配实时性要求,减少控制分配中的抖振现象,使得控制量平稳,减少不必要的控制量饱和,取整体精度权值Wu为变权值,其更新策略为
Wu(k+1)=Wu(k)+ηΔWu(k)
(45)
控制目标是使误差滑模面趋于0,使用梯度下降法进行在线自适应调整,即
(46)
式中,si为误差滑模面;η为自适应调节因子,表示为
(47)
整个控制系统如图3所示。
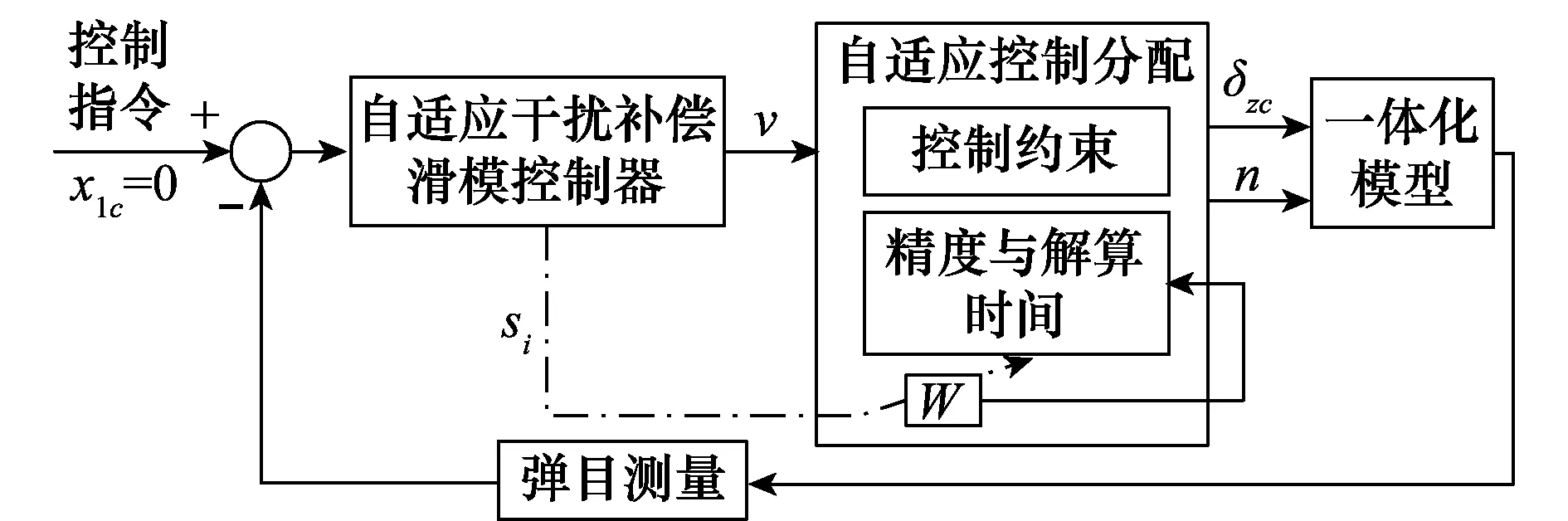
图3 控制系统结构图Fig.3 Structure of control system
控制分配算法本质上属于迭代算法,由于控制系统实时性要求较高,设计迭代终止条件为分配权值限制和迭代次数限制,即
(48)
式中,β为容忍的权值限;M0为最大迭代次数。若系统以增大的速度远离滑模面,则按照梯度法增大整体精度权重Wu,此时使得权值变化大,系统更易达到权值限制,从而提高实际控制力矩对虚拟控制力矩的跟踪精度,并使算法易收敛,提高实时性,使系统快速趋于滑模面;若误差面增长较缓慢,则对实时性要求不高,可充分寻优。控制分配策略能使系统逼近所要求的虚拟控制力矩。
2.3 系统稳定性分析
定理1对于不确定系统式(15),采用ESO对复合干扰d1、d2和d3进行观测,使用在线自适应律式(24)、式(30)和式(38)对观测误差进行补偿,并取滑模控制律式(39),则闭环系统的状态跟踪误差将在有限时间内收敛至原点附近任意小的紧集,x1趋于0。
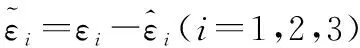
取准Lyapunov函数
(49)
式(49)对时间求导得
(50)
将式(22)、式(23)、式(26)、式(28)、式(29)、式(34)、式(36)、式(37)代入式(50),得
(51)
将在线自适应律式(24)、式(30)和式(38)代入式(51),并由观测误差有上界可得
(52)
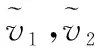
(53)
必存在非负的连续函数ξj(j=1,2)使得
(54)
将式(54)代入到式(53)可得
(55)
由式(53)和式(55),可得
(56)
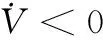
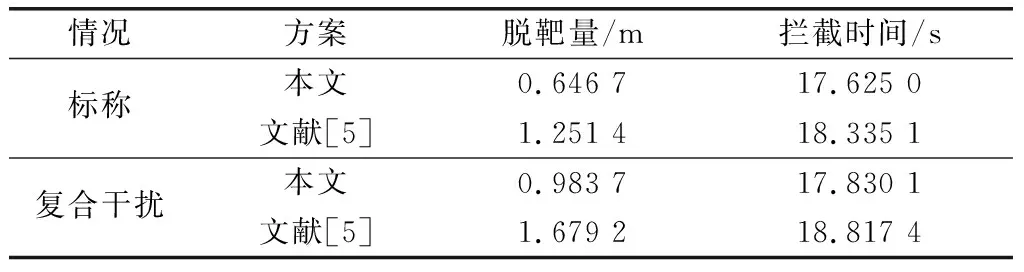
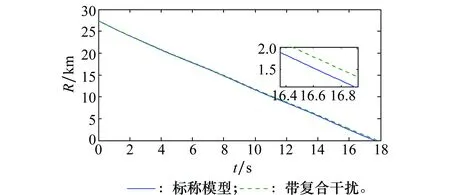
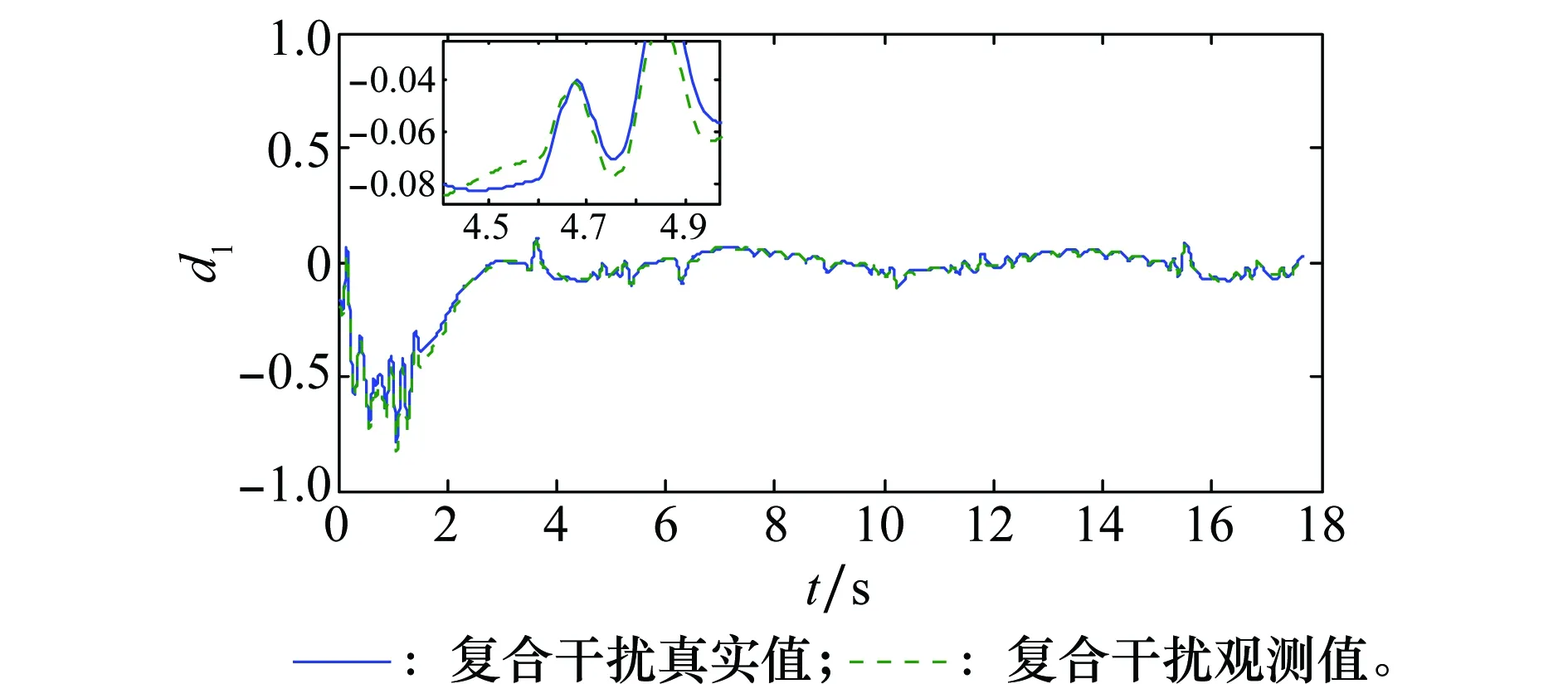
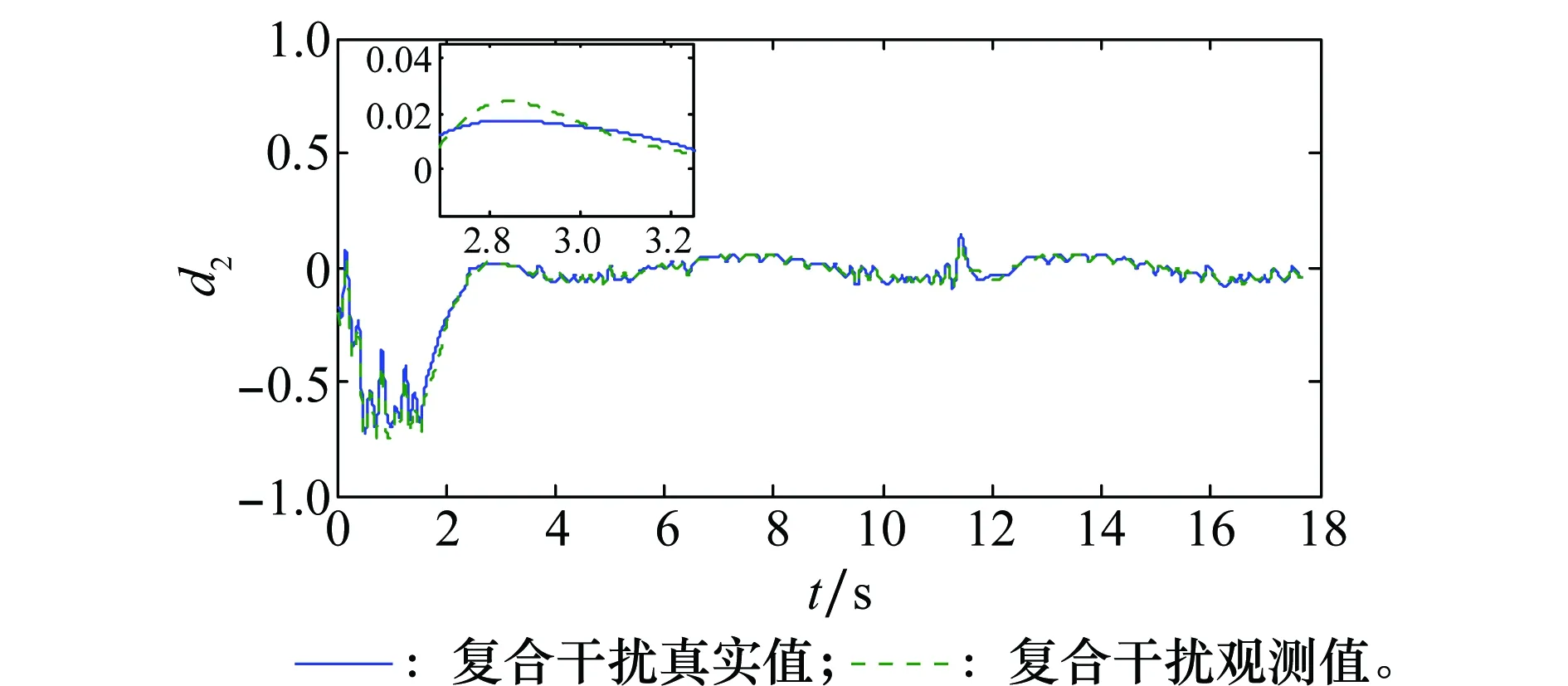
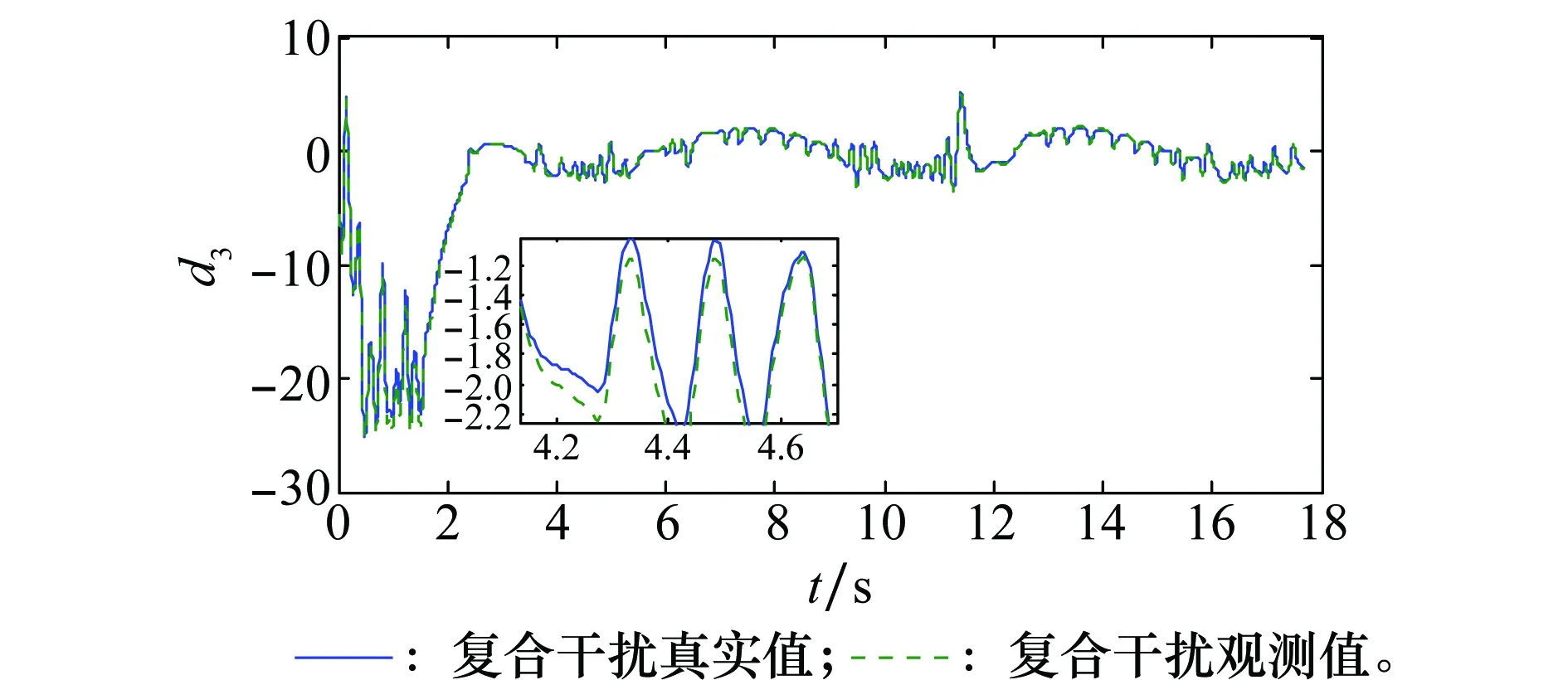
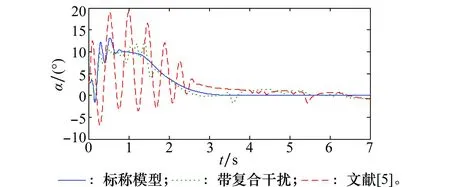
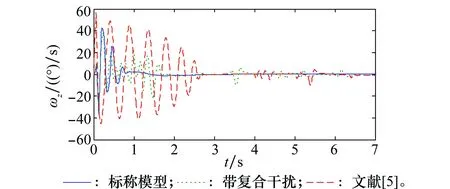
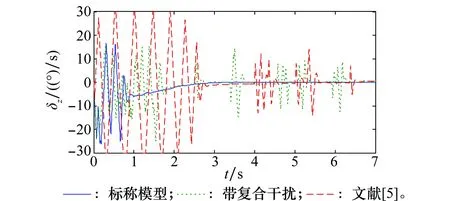
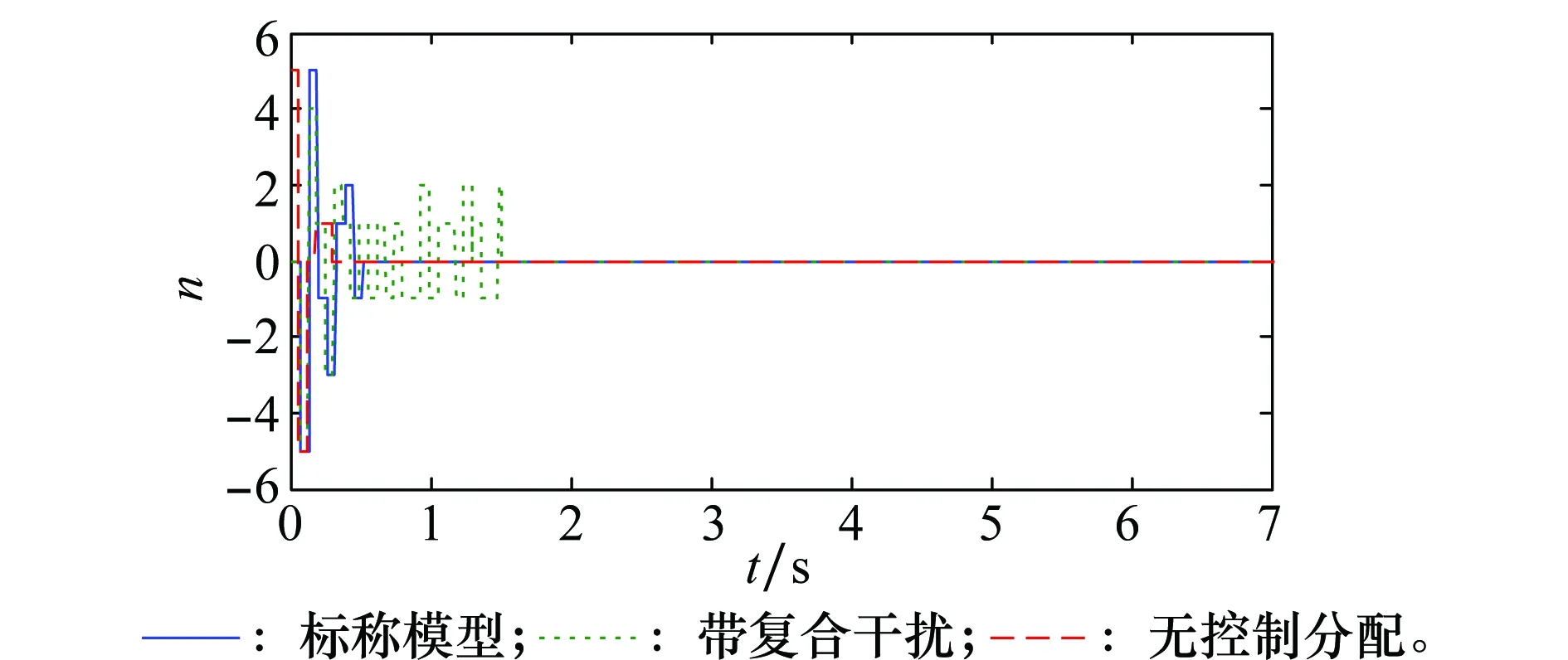
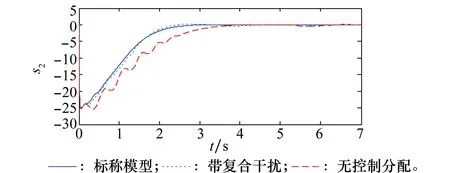
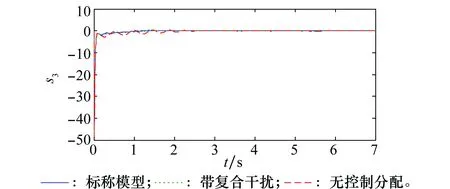
应用Young不等式ab (57) 将式(56)和式(57)代入到式(52)可得 (58) 取滤波器时间常数τi足够小,则 此时有 则式(58)退化为 (59) (60) 将式(60)代入到式(59)可得 这意味着系统跟踪误差si最终有界稳定,并满足 至此,可以证明闭环系统一致最终有界,误差收敛至距离原点任意小的邻域,且此邻域大小与有界复合干扰无关,仅由控制器设计参数决定,最终使得x1→0。 证毕 为验证本文提出了控制方法及分配策略的正确性、高精度,针对如下模型进行仿真验证。 导弹速度初始速度1 197 m/s,初始弹道倾角θM0为30°,初始攻角α(0)为10°,俯仰角速率ωz(0)为0,导弹初始位置为(xM,yM)=(0 m,11 000 m);目标初始速度为926 m/s,初始弹道倾角θT0为160°,目标初始位置为(xT,yT)=(23 000 m,28 000 m)。导弹标称气动力参数为 设计控制器参数k1=29,k2=1.6,k3=1.6,自适应律参数为 c1=c2=c3=1.5;γ1=γ2=1 γ3=0.01;ρ1=ρ2=ρ3=0.000 1 ESO参数为 β11=β21=β31=5;β12=β22=β32=30 μ11=μ21=μ31=0.25;δ1=δ1=δ1=0.2 分配策略权重取为:Wn=1,Wδz=0.1,Wu初值取Wu(0)=100,其他参数取κ=-0.1,权值限β=1.2,最大迭代次数M0=500。 对本文提出的方法在标称情况下和存在复合干扰情况下分别进行仿真。标称情况综合扰动信号d1=d2=d3=0;复合干扰包括气动参数存在±20%不确定性,目标以6g振幅、周期3/π正弦机动,喷流干扰d11=0.1sin(πt/2),d21=0.2sin(πt/2)和d31=0.1sin(πt/2)。 使用文献[5]中的无控制分配的自适应反步滑模控制设计方法作为对比,表1和图4~图14为结果对比。 表1 脱靶量和拦截时间 图4 弹目相对距离RFig.4 History of missile and target relative distacnce R 图5 复合干扰d1Fig.5 History of disturbance d1 图6 复合干扰d2Fig.6 History of disturbance d2 图7 复合干扰d3Fig.7 History of disturbance d3 图8 攻角αFig.8 History of attack angle α 图9 俯仰角速率ωzFig.9 History of pitch rate ωz 图10 升降舵偏角δzFig.10 History of deflection δz 图11 直接脉冲力Fig.11 History of pulse engine 图13 滑模面s2Fig.13 History of surface s2 图14 滑模面s3Fig.14 History of surface s3 由表1和图4可以看出,本文提出的一体化控制及控制分配策略具有较小的脱靶量,并能快速拦截目标。 图5~图7为复合干扰观测曲线,可以看出,本文设计的ESO能够准确估计系统中存在的随机扰动,说明ESO对随机扰动观测较为精确且具有鲁棒性。 图8~图10分别为攻角、俯仰角速率、升降舵偏角响应曲线,可看出文献[5]无控制分配的滑模反步设计方法响应量大,变化剧烈,且舵面存在饱和现象;而本文提出的方法,攻角、俯仰角速率、舵偏角响应明显减小且变化平缓,无饱和现象;图11为直接力使用情况,直接脉冲力在存在复合干扰时动作频繁,而文献[5]直接求解出的控制量未充分利用直接力,导致舵偏饱和。 图12~图14为设计的滑模面响应曲线,本文设计方法快速收敛且无增长,最终趋近于零。 综上,本文设计方法能够使得导弹快速精确打击到目标,自适应干扰补偿能够使系统对复合干扰具有鲁棒性,自适应控制分配避免了反复设计,减小了舵偏量,使得系统状态量响应小,变化平滑,滑模误差面无震荡较快收敛。 本文针对直接力/气动力复合控制导弹的IGC问题,设计ESO对系统复合干扰进行观测,构造自适应误差滑模面补偿观测误差,并使用反步法设计控制器,实现对复合干扰的抑制。 本文提出一种自适应控制分配方法,综合考虑控制的实时性和精度要求,使用滑模误差对控制分配权值进行在线自适应调整,设计算法迭代终止条件,在误差增大时提高实时性和分配精度,加快系统收敛。 仿真结果表明,所设计的广义控制律和控制分配策略可以对复合干扰进行补偿,使得动态过程较为平滑,控制量较小,提高了系统鲁棒性,脱靶量较小。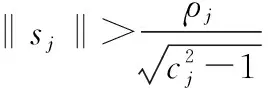
3 仿真验证
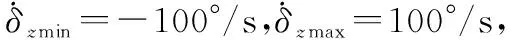
4 结 论
