软件缺陷传播的概率模型研究

何睿，张力生

（重庆邮电大学软件工程学院，重庆 400065）

0 引言

随着科技、经济的高速发展，我们早已进入大数据时代，软件已是人们生活不可或缺的技术。现在，人们的需求相较于以往更加丰富而多样，使得软件开发的规模更加庞大而复杂，以开发出满足需求的软件。软件质量保证[1]是评判软件开发的重要标准，与客户满意度直接相关，决定软件项目是否成功[2]。软件质量保证的主要方式是排除软件缺陷。

IEEE 729-1983对软件缺陷有一个标准的定义：从产品内部看，缺陷是软件产品开发或维护过程中存在的错误等各种问题；从产品外部看，缺陷是系统所需要实现的某种功能的失效或违背。错误是人为错误，指软件开发人员在开发软件的过程中无意间犯下的技术错误，失效是软件运行时不能完成规定功能[3]。正是错误导致软件工作产品的失效。

从广义来说，软件的本质是软件开发过程的所有结果，即文档、程序、数据；从狭义的软件运行的角度而言，软件是可以在图灵机等计算模型上可以运行的计算机语言（程序），是计算机模型可运行的操作序列。按照图灵机理论，每一个操作序列对应着图灵机的一个格局。当图灵机的一个格局出错时，软件的运行就无法得到正确的输出结果，则没有达到用户对软件系统的期望，表现为软件缺陷。

本文首先将软件抽象为一棵函数树，并讨论函数树的叶子结点、操作序列，以及操作序列对应图灵机格局，建立了软件缺陷的传播概率模型，通过稳定性理论求解出系统的平衡点，并分析了平衡点的局部稳定性和全局稳定性。

1 软件与函数树

结合软件开发方法中抽象与分解的思想，软件开发过程是对软件不断细化的过程。每一次的细化抽象为一个函数，函数之间的关系为细化的逻辑关系。函数为顶点，函数与函数之间的关联为边，构建了一棵描述软件本质的函数树。根据软件的生命周期理论，将软件的生命周期分为需求、分析、设计、实现、测试、维护6个阶段，图1表示了6个阶段与函数树的大致对应关系。

需求分析阶段，主要任务是使用恰当的工具，分析获取用户对系统将提供的服务要求，即是对复杂而大型软件系统进行高粒度地抽象与分解的过程。

分析设计阶段，主要任务是根据需求阶段的结果，采用不同的方法与恰当的工具，分析和设计出软件逻辑构成。有很多分析设计工具，但面向对象分析设计方法及UML工具已成为主流。

图1 函数树软件生命周期的划分示例

实现阶段，编码实现阶段的主要任务是基于分析设计的结果，使用计算机语言编写程序，从本质上讲，定义在计算机上能够运行的操作序列，以实现预期的功能。多采用面向对象程序语言作为工具，而面向对象程序语言仍然可分为面向对象和过程式编程两部分，最终都要使用过程式编程部分定义操作序列。

2 软件缺陷传播概率模型

软件缺陷改变在函数树上叶子结点，操作序列所对应的格局状态的过程如下：

根据上述格局状态的改变过程，结合文献[4-5]的建模思想、思路及方法，以一个格局为一个结点，构建了软件缺陷传播概率模型。模型将结点状态划分为三个状态：无缺陷状态S（没有缺陷的结点），缺陷潜伏状态L（有缺陷但是还未被发现的结点）和缺陷暴露状态A（有缺陷且已被发现的结点）。在任意时刻t，每个结点只能处于上述状态中的任意一种。分别用S(t)，L(t)和A(t)表示t时刻处于S状态，L状态和A状态的结点密度，为方便起见，分别简写为：S，L，A。

根据实际软件开发过程中软件缺陷的传播过程，为建立结点函数缺陷状态传播模型，给出如下假设：

①大型复杂软件系统的软件函数结点数量是恒定；

②在开发过程之初，开发人员未进行任何开发活动，没有错误产生，结点初始状态为无缺陷状态S；

③在开发过程的迭代中，S状态结点通过每个成员失误变为L状态的概率相等为ε()t；

④在开发过程的迭代中，由不同成员之间协作时失误的影响，S状态结点变为L状态的概率相等为 θ(t)；

⑤在测试阶段，假设测试人员发现缺陷的概率为α，即L状态结点转变为A状态结点的概率为α；

⑥测试人员发现软件缺陷后，假设开发人员消除缺陷使得软件变为无缺陷状态的概率相等为γ，即为γ；

⑦测试人员发现软件缺陷后，开发人员修复有缺陷状态结点时因错误而产生新潜在缺陷状态的概率相等为δ，即A状态结点转变为L状态结点的概率相等为δ。

根据上述假设，如图2所示。其中，状态S转换成状态L的概率：

图2 软件缺陷状态传播模型

微分方程为：

设Anew为可以传递缺陷的节点数，r为传递对象的平均数。根据软件缺陷与开发过程的关系可得，时间间隔Δt内，节点由S状态转变为L状态的数目是：

根据状态模型有：在时间间隔Δt内，节点由S状态转变为L状态的数目是：

其中，N是节点总数。

将方程（1）和（2）结合起来计算可得：

同时，根据状态模型，可以传递缺陷的节点数Anew为：

结合方程（3）和（4）计算，可以得到V(t)的表达式：

根据假设（1）可知：

将方程（6）和（7）代入系统（1）中，系统（1）可化简为：

由于L代表了t时刻处于L状态的节点密度，A代表了t时刻处于A状态的节点密度，由公式（7）可知系统（7）的正向不变集Ω为：

3 模型分析

3.1 平衡点

定理1：系统有唯一的有缺陷平衡点E*=(L*,A*)，其中：

证明：为了获得系统（8）的平衡点，系统（8）必须满足如下方程：

整理方程组（12），可得：

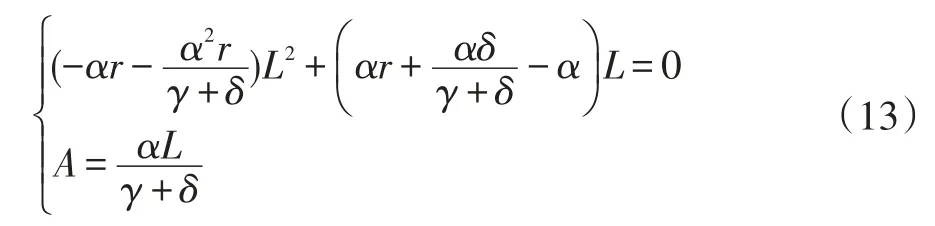
显然，方程组恒有如下解：

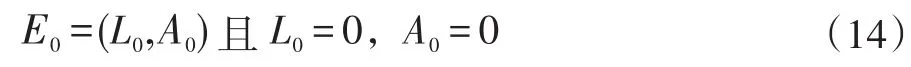
因为E0中L0和A0均为0，所以平衡点E0是无缺陷平衡点，且系统始终存在无缺陷平衡点E0。这意味着S0=1-L0-A0=1，代表系统（8）在无缺陷的情况下各节点的存在状态。

通过计算，方程组另有一非零解：

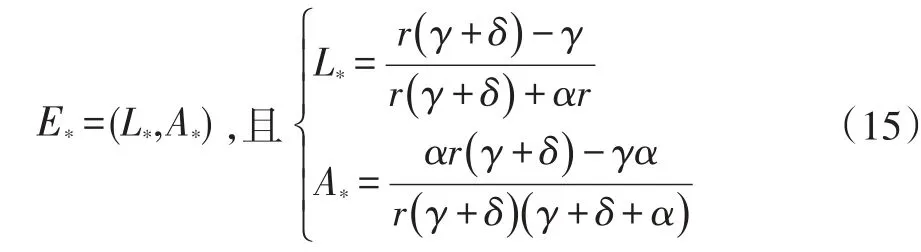
在无缺陷平衡点E0=(L0,A0)处线性化系统对应的特征方程为：

其中：

通 过 公 式（17）可 以 看 出 a＞0 ，c＞0 ，且根据一元二次方程根与系数的关系可知公式（16）必有一根大于0，方程即该线性系统的特征根不全具有负实部，根据Lyapunov定理[6]，平衡点E0不稳定。根据稳定性理论可知，系统只有唯一的有缺陷平衡点E*。

3.2 局部稳定性分析

定理2：有缺陷平衡点E*局部渐进稳定。

证明：系统在平衡点E*处的Jacobian矩阵为：

其所对应的特征方程为：

其中：

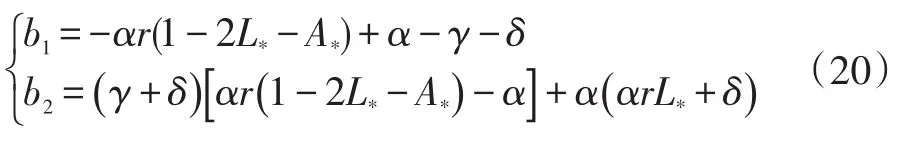
将 S*=1-L*-A*代入方程（4.3）的 L˙=0 中，可得：

于是，将等式（21）代入b1，b2中，则：

3.3 全局稳定性分析

定理3：有缺陷平衡点E*是全局渐近稳定的。

证明：考虑如下函数[7]：

根据系统（8）计算可得：

4 结语

本文给出了描述软件本质的数学模型、函数树。以函数树的叶子结点对应图灵机的格局，以一个格局为讨论对象，构建了软件传播概率模型。软件最开始是没有缺陷的，随着软件开发工作的进行，格局状态变为有缺陷的状态，通过测试工作软件缺陷会被消除，也会产生新的缺陷。

基于软件缺陷概率传播模型，使用微分动力系统理论其进行分析，推导出软件缺陷概率传播模型存在唯一的有缺陷平衡点，同时分析证明该平衡点不仅局部稳定，而且全局稳定，从理论上证明了这意味着开发过程中的软件缺陷将无法根除。