障碍环境下线段反k最近区域查询方法研究*
2018-10-12张丽平任玲玲郝晓红
张丽平,任玲玲,郝晓红,李 松
哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
1 引言
近年来,随着智能识别系统、地理信息系统、交通网络系统等的广泛应用,空间数据查询技术具有越来越重要的作用。近邻查询是空间数据库中的重要查询类型。近邻查询包括许多种类:最近邻[1](nearest neighbor,NN)查询、k最近邻[2-4](knearest neighbor,kNN)查询、反向最近邻[5-6](reverse nearest neighbor,RNN)查询、线段最近邻[7](line nearest neighbor,LNN)查询、组最近邻[8](group nearest neighbor,GNN)查询等,研究成果解决了最近邻查询领域的一系列重要问题。
反k最近邻[9](reverseknearest neighbor,RkNN)查询是k最近邻查询的一个重要变体,获得将查询对象作为k最近邻的数据对象集合。RkNN查询通常反映出查询点对哪些空间数据点影响较大,因此一般用来评估查询对象的影响力。例如,游客出去度假(多为海边或是山等),可以根据对其周边设施的反k最近邻查询,来获得合理的旅游方案。由于山脉、海、湖泊等不适合抽象为点或线段,但可以抽象为不规则图形。由于其他景点或道路形成的障碍,因此需要考虑障碍环境下的线段反k最近区域的查询方法。
国内外对无障碍空间下的kNN查询和RkNN查询以及障碍空间的kNN和RkNN查询进行了一些重要研究。针对于无障碍空间的kNN查询问题,文献[10]中为了有效查询和更新给定点的最近邻,研究了基于空间网格的Voronoi图的方法,并提出了相关算法。文献[11]进一步考虑查询结果的可用性,制定一个新的查询类型MkDNN(movingkdynamic nearest neighbor),并且提出了一种增量维护k多样性最近邻算法。文献[12]利用Voronoi图预计算的优势,可以解决kNN查询,并提高了用户的查询效率。针对无障碍空间的反向k最近邻(RkNN)查询问题,文献[13]提出了反向最近邻的搜索方法,考虑反方向的查询对象和目标对象之间的位置。文献[14]提出了基于距离的方法可以在高维环境中产生更多的对比离群分数。采用经典的k-NN的评价方法,提出了基于无监督距离的离群点检测中的反向最近邻。文献[15]提出了一种新的剪枝方法,该方法使用了一个多边形近似未被剪枝的区域。
针对障碍环境下的kNN查询问题,文献[16]提出了一个地区的障碍处理MkNN(movingknearest neighbor)查询方法,介绍和采用高效MkNN处理算法。文献[17]主要提出障碍空间中的连续反k近邻查询问题。通过定义控制点和分割点,提出了针对该问题的处理框架。进一步地,提出了一系列的过滤和求精算法,包括剪枝数据集、获取障碍物、剪枝和计算控制点和更新结果集等处理策略。文献[18]通过有效的对象之间的路径,提出了障碍环境下的连续kNN查询的优化方法。针对障碍空间下的RkNN查询问题,文献[19]提出了剪枝算法,优化障碍反向最近邻查询算法。文献[20]提出了一种基于Voronoi图的剪枝方法,根据Voronoi图和障碍距离的特性,减少了数据点处理个数。
目前的空间查询方法仅限于对象为点或是线段的近邻查询,并没有涉及到障碍空间下的线段最近区域。因此,在障碍空间中,如何查询反向线段最近区域是一个新问题。为了有效解决该问题,本文首次提出了障碍环境下的反k线段最近区域查询方法。该方法首先对数据区域集进行约减,缩减了查询的搜索范围。然后根据剪枝过程所提定理对候选集进行过滤,获得更精确的候选集。最后根据Voronoi图的性质提出相关定理,精炼OLRkNR(obstacle line reverseknearest region)查询的结果集。
2 定义及性质
在给定的数据空间内,存在着区域和障碍物,其中区域为不规则图形,障碍物为线段形状。设障碍线段为O={o1,o2,…,om},区域集Rs={r1,r2,…,rn}以及一个查询线段l。障碍物与区域之间不相交,即O={o1,o2,…,om|Oi=oi1oi2,oi1oi2⋂rj=∅ ,i∈[1,m],j∈[1,n]}。
基于线段Voronoi图[21]和点与线段之间的最近距离[22]的定义,本章进一步给出障碍线段反k最近区域查询、线段区域最近距离和线段区域Voronoi图等定义。
定义1(线段障碍最近距离)已知查询线段L和障碍物O,点li,lj,l∈L,点oi,oj,o∈O,dist(l,o)表示点l到点o的距离,则线段L与线段O的最近邻距离为dist(L,O)={dist(li,oi),dist(li,oi)≤dist(lj,oj)}。
定义2(线段与区域的可视性)给定一个查询线段l,区域r∈Rs和障碍物集O,l和r是可视的当且仅当l的两端点与r形成的不规则图形与O中任何障碍都不相交,即o∈O,[l,r]⋂o=∅ 。
定义3(线段区域最近距离)障碍空间中存在查询线段l,设其左右两端分别为m和n。若线段与区域可视,则线段与区域的欧式距离即为最短可视距离distv(l,r),则障碍距离等于线段与区域的最短可视化距离disto(l,r)=distv(l,r);若两线段之间完全不可视,则线段区域之间的障碍距离为线段区域绕过障碍物的最短距离。即disto(l,r)=min{dist(m,oi1)+dist(r,oi1),dist(n,oi2)+dist(r,oi2)}。
定义4(障碍线段反k最近区域查询,OLRkNR)在障碍空间中,给定一查询线段l,互不相交的生成区域集合Rs={r1,r2,…,rn}和一个整数k,当一个对象r∈Rs在Rs上的kNN的结果包括L中的任意一个时,r是OLRkNR(Rs,L,k)的一个结果,具体形式为:OLRkNR(Rs,L,k)={∃l∈L,∃r∈Rs|l∈kNN(l,k,Rs)}。
定义5(线段区域Voronoi图,line region Voronoi diagram,LRVD)给定一组互不相交的生成区域集合Rs={r1,r2,…,rn}和生成线段L={l1,l2,…,lm},节点集合P={p1,p2,…,pi},边的集合E={e1,e2,…,ek}。令rj为不同于ri的生成区域,lj为不同于li的生成线段,线段区域Voronoi图将平面分成若干区域,则线段li或区域ri所在的区域称为LRVP(line region voronoi portion)。则LRVP(li,ri)可以形式化表示为:LRVP(li,ri)={l,r|r∈Rs,l∈L,dist(r,ri)≤dist(r,rj),dist(l,li)≤dist(l,lj)}。
若区域集合Rs中的每一个区域和数据线段集中的线段L都可以生成一个LRVP,则LRVD由n+m个LRVP组成,因此可以定义LRVD:LRVD(Rs,L)={LRVP(r1),LRVP(r2),…,LRVP(rn),LRVP(l1),LRVP(l2),…,LRVP(lm)}。
由线段区域Voronoi图的结构和定义可以得出以下性质:
性质1(最近邻特性)生成区域ri的最近邻必存在于与LRVP(ri)邻接的LRVP中。
性质2(线性特性)令生成区域ri,生成线段li和Voronoi棱的数量en,则en≤3(ri+li)-6。
根据区域Voronoi图的定义及性质,进一步提出了线段区域Voronoi图生成算法,如算法1所示。
算法1Create_LRVD(L,Rs,E,N)
输入:区域集Rs,边集合E,节点集合N,数据线段集L。
输出:LRVD。
begin:
1.根据数据线段集L生成线段Voronoi图;
2. 令l∈L,使l′//l且l′交ri于点q,设l′的左右端点分别为a、b;
3.过节点n做l′的垂线,垂足为o;
4.ifo∈rithen
5.dist(ni)=dist(ni,o);
6.elseo∉ri
7.dist(ni)=dist(ni,q);
8.end if
9.ifdist(ni,ri) 10.ni∈LRVP(ri); 11.end if 12.for each(ni,nj)∈E 13. if(ri⋂rj=null)then 14. 计算LRVP(ri)与LRVP(rj)边界点 15.h=(ni,nj|dist(ni)-dist(nj)-dist(ni,nj)/2)的位置; 16.end if 17.end for 18.return LRVD; End 定理1算法Create_LRVD能正确地求出LRVD,其时间复杂度为O(nlgn)。 证明(正确性)令dist(ni,ri)为节点ni到区域ri的最短距离,其中ni存在于LRVP(li)中。当k=1时,有dist(ni,r1)≤dist(ni,ri),则节点ni的反向最近区域RNR(reverse nearest region)为r1,即线段li的RNR为区域r1。当k>1时,令dist(ni,rk)≤dist(ni,ri),0 (时间复杂度分析)该算法首先生成线段Voronoi图的时间复杂度为O(nlgn)。for循环的执行次数为n次,时间复杂度为O(n)。该算法总的时间复杂度为O(nlgn+n)。故该算法的时间复杂度为O(nlgn)。 □ 数据集包含区域集、障碍物集。基于Voronoi图的性质和结构提出了定理2。根据定理2,去掉非候选者集合,获得候选集合。该过程减少了大量的数据集合,缩小了查询范围。 定理2给定一组区域集Rs和查询线段l,则计算出到查询线段l经过的最少区域个数小于或等于k的区域ri存在于候选集中。 证明令count(r,l)为区域r到查询线段l需要经过最少的区域个数。当k=1时,相当于查询线段l的反向最近区域(RNR),则l的RNR的区域r是查询线段l的Voronoi邻居,即区域r满足count(r,l)≤1;当k≥1时,令count(ri,l)≤i,0≤i≤k,则count(rk+1,l)≤k+1。根据线段Voronoi图[21]定义可知,rk+1是ri∈{r1,r2,…,rk}中的一个Voronoi邻居。即:count(rk+1,l)≤max(count(r,ri)+1)≤k+1,故定理2成立。 □ 根据定理2,本节给出算法OLRkNR_Reduct,其主要思想为:将查询线段l的前k级邻接区域放入候选集Rl中,而高于k级的邻接区域则约减。该过程首先根据障碍物集合生成线段Voronoi图,判定l的位置。最后依据l的位置进行数据区域约减。 基于以上讨论,本文进一步给出了约减数据集算法,如算法2所示。 算法2OLRkNR_Reduct(l,Rs,O,k) 输入:查询线段l,区域集Rs,障碍物集O,k值。 输出:约减的区域候选集Rl。 begin: 1.Rl←null;/*初始化候选集Rl为空*/ 2.Create_LRVD(l⋃O); 3.fori=1tokdo 4.ifl∈LRVP(ri)then 5.Rl←Rl+ri;/*将l的第一个反向最近区域加入到Rl中*/ 6.end if 7.else ifri与l是邻接的then 8.Rl←Rl+ri; 9.end if 10.ifcount(ri,l)≤kthen 11.Rl←Rl+ri; 12.end if 13.end for 14.returnRl; End 定理3算法OLRkNR_Reduct是正确的,其时间复杂度为O(nlgn)。 证明(正确性)根据定理1,已经证明创建LRVD是正确的。假设查询线段为l,令该算法返回的区域为ri,且ri不是l的反向最近区域对象。令rk(l)为线段l的反向最近区域对象,dist(rk(l),l)表示l的RNR的距离。如果ri不是l的RNR,则必有dist(rk(l),l) (时间复杂度分析)该算法生成线段Voronoi图的时间复杂度为O(nlgn)。for循环的执行过程是k次,k远小于n,故算法2的时间复杂度为O(nlgn)。□ 该过程主要对候选集Rl进行过滤,剪枝掉大量非候选集,获得更精确的候选集。为了有效进行剪枝,提出了定理4、定理5。 定理4令区域r在查询线段l的最近邻的第n级邻接生成区域中,且r到l的路径上经过的区域个数小于等于n,即sumcount(r,l)≤n。若sumcount(r,l)≥k,则区域r被剪枝。 证明令ri为区域r到查询线段l之间经过的若干对象。当区域r到查询线段l之间不存在障碍物时,则可以知道ri到l一定比r到l的欧氏距离近;当区域r到查询线段l之间存在障碍物时,那么ri到l的距离也一定比r到l的距离近。当k=1时,显然dist(ri,l)≤dist(r,l)。当k>1时,ri的个数不小于k个,那么r的k最近邻不包含l,即sumcount(r,l)≥k时,r一定不是候选集里的对象。 □ 定理5给定任意r∈Rl,若r的Voronoi邻居都被剪枝了,则区域r也被剪枝。 证明令r为候选集Rl中的任意区域且r的Voronoi邻居都被剪枝。由线段Voronoi图的性质可知,查询线段l到r一定会经过r的Voronoi邻居rv。若无障碍无环境下l到ri之间的区域数目为NoObs_Count(rv,l)≥k,因此NoObs_Count(r,l)≥k+1≥k。由定理4可知,区域r被剪枝。 □ 根据定理4、定理5,进一步给出了剪枝算法Prune_Neighbor,如算法3所示。 算法3Prune_Neighbor(Rl,l) 输入:候选集Rl,查询线段l。 输出:剪枝后的候选集Rl。 1.Rl←null;/*初始化候选集为空*/ 2.Rl←OLRkNR_Reduct( )l,Rs,O,k; 3.PruneFlag=true; 4.for eachrjinRldo 5.for eachrj∈VN(ri)do 6. ifrj∈Rlthen 7. PruneFlag=false; 8. end if 9.end for 10.end for 11.if PruneFlag=true then 12.Rl←Rl-ri; 13.end if 14.end for 15.returnRl; End 定理6算法Prune_Neighbor是正确的,其时间复杂度为O(nlgn)。 证明(正确性)该算法首先调用了算法2,定理3已经被证明是正确的。然后依据PruneFlag为true来标记对象是需要剪枝的。判断区域rj是否在VN(ri)中,如果不在则直接剪枝掉。该算法可以正确找到剪枝后的候选集合。故该算法是正确的。 (时间复杂度分析)该算法执行算法2的时间复杂度为O(nlgn)。执行两个嵌套for循环的最坏时间复杂度为O(mn)(m远小于n),故该算法的时间复杂度为O(nlgn+mn),化简为O(nlgn)。 □ 本文提出的精炼过程主要针对候选集Rl进行处理,得到最后的查询结果。首先依据Voronoi图的性质与定理提出了定理7。根据定理7对候选集中的区域进行处理。该过程可得到更精确的候选集。 定理7给定查询线段l,区域r∈Rl,区域r的质心为m。当查询线段l与r是可视的,则以查询线段l的中点pmid为圆心,以diste(pmid,m)为半径画圆,将判定圆内r可视的数据点个数设为sum_regions,如果sum_regions≥k,则r被剪枝。当查询线段l与r是不可视的,以查询线段l的中点pmid为圆心,以disto(pmid,m)为半径画圆。同理,如果sum_regions≥k,则r被剪枝。 证明(1)当r∈Rl且r对查询线段l可视时,首先设置OLRkNR中的k值为2。如图1所示,以点pmid为圆心,以dist(pmid,m1)为半径画圆。其中,pmid为线段l的中点,m1为区域r3的质心。则由图可看出,在判定圆中的区域有{r1,r2},因此sum_regions=2=k,显然r3的2NN是{r1,r2},不包含查询线段l,则查询线段l的RkNR一定不包含r3,则r3被剪枝。 Fig.1 Example of proof 1 based on theorem 7图1 基于定理7证明情况1的示例 (2)当r∈Rl且r对查询线段l1不可视时,如图2所示。以查询线段l1的中点pmid为圆心,以disto(pmid,m1)为半径画圆,则在判定圆中的区域有{r1,r2,r4}且对查询线段l1都是可视的,则sum_count=3。当k=3时,显然r3的3NN是{r1,r2,r4},不包含线段l1。当k<3时,区域{r1,r2,r4}到r3的距离一定小于查询线段l1到r3的距离,故r3的kNN是{r1,r2,r4}中的k个,一定不包含查询线段l1。故查询线段l1的RkNR一定不包含区域r3,因此将r3剪枝。 □ Fig.2 Example of proof 2 based on theorem 7图2 基于定理7证明情况2的示例 根据定理7,提出了精炼算法Refine_OLRkNR,该方法查看区域集Rs中的ri和查询线段l。当r与l之间有大于k个无障碍物的对象,那么r被剪枝。 基于以上论述,进一步给出了精炼算法,如算法4所示。 算法4Refine_OLRkNR(Rl,l,O,k) 输入:候选集Rl,查询线段l,障碍物集O,OLRkNR中的k值。 输出:约减的候选集Rl。 begin: 1.Rl←null;/*初始化候选集为空*/ 2.Rl←Prune_Neighbor(Rl,l); 3.sumcount=0; 4.令m为区域r的质心,pmid为查询线段l的中点; 5.令C(r)以dist(pmid,m)为半径的圆 6.for eachriinRldo 7.for eachrjinRl⋂C(r)do 8. ifrj与l之间无障碍物then 9.sumcount←sumcount+1; 10. end if 11. else ifrj与l存在障碍物且大于kthen 12.Rl←Rl-r; 13. end if 14.end for 15.end for 16.returnRl; End 定理8算法Refine_OLRkNR是正确的,其算法复杂度为O(nlgn)。 证明(正确性)该算法首先调用算法3,根据定理6可知,算法3是正确的。然后对于候选集中的每个区域r,以区域r中的质心m为圆心。令查询线段中点pmid,则dist(pmid,m)为半径的圆C(r)。如果在候选集中的区域r也在这个圆中,那么判断l与r之间是否存在障碍物。若对于r与l之间有多于k个障碍物,则r被剪枝。故该算法是正确的。 (时间复杂度分析)该算法执行算法Prune_Neighbor的时间复杂度是O(nlgn),执行两个嵌套for循环的最坏时间复杂度为O(nlgn),故该算法的时间复杂度为O(2nlgn),化简为O(nlgn)。 □ 本章通过实验对算法Refine_OLRkNR进行性能分析。由于已有的研究成果无法直接处理障碍环境下的线段反k最近区域查询问题,为了得到比较算法,分别对文献[20]所提的RkNNobs算法、文献[23]提出的LNN_Search算法以及文献[24]提出的STA_RVLRkNN(static_road voronoi line reverseknearest neighbor)算法为基础,将这3种算法进行适当的调整。根据文献[20]设计了第一个较为基础的算法RkNNobs_Basic,将该算法中的输入查询点、障碍物集合调整为线段输入,将对象点集合调整为不规则图形输入。文献[23]设计了第二个基础的算法LNN_Basic,反复调用LNN_Search算法,并在Voronoi图中随机生成区域集合。根据文献[24]设计了RVLRkNN_Basic算法,在Voronoi图中随机生成区域集合并在线段集合中随机设定为障碍集合。 本实验环境设置:2.0GHzCPU,4GB内存,500GB硬盘,Windows 7操作系统。实验采用的数据是美国旧金山和加州的路网信息[25],该实验数据集包含1955206个节点,2766607条无向边,其中交叉点和端点由节点表示,连接这些交叉点或道路端点则由无向边表示。实验中,对数据分布进行了适当调整,障碍集O和区域集Rs是由随机生成器产生的均匀分布的线段以及不规则图形数据。此外,用A表示子区域占整个路网的百分比。参数F表示边的权值与实际长度的偏离程度,F=权值/欧氏距离。在默认情况下,每次查询5的倍数个查询区域,分布在A=5%的路网中,目标区域的密度P=0.05,参数F=2。实验测试的指标为CPU时间、I/O代价影响以及准确率,并取200次查询的平均结果。 如图3所示,首先分析k值对CPU时间的影响。实验采用的是真实数据集,查询线段数量为50,区域数量为5000,障碍物数量为1000。图3给出了4种算法的CPU时间随着k值变化的对比结果。随着k值的不断变大,算法的CPU时间均呈上升趋势。LNN_Basic算法需要对区域集中的每个区域都计算它的kNN,随着k的增加,造成了搜索区域大量重叠的情况,从而使得查询时间较长。RkNNobs_Basic算法将空间分为6等份,然而某些区域可能横跨两个空间,则会造成搜索区域的重叠,降低了查询性能。RVLRkNN_Basic算法并不能优化障碍物集合,这使得k值在增加时,搜索过程中障碍物的数量会增加,降低了查询速度。而本文提出的OLRkNR查询算法在约减数据集过程中就排除了大量的非候选数据集,之后又通过剪枝过程和精炼过程得到了精确的查询结果,有效缩小了查询范围。因此查询所用时间比其他3组对比算法要少。 Fig.3 Effect of k on CPU time图3 k值对CPU时间的影响 进一步分析k值的变化对算法I/O代价的影响。如图4所示,3种对比算法的I/O代价随着k值的增长,上升趋势比较显著,而OLRkNR算法相对来说I/O代价趋势较为平缓。这是因为LNN_Basic算法需要计算每一条线段的线段最近区域,随着k值的增加算法在查询过程中所要访问的区域也逐渐增多,从而造成算法的I/O代价较高。RkNNobs_Basic算法在将空间划分为6等份后,随着k值的增加,在查询过程中重复搜索的区域也会变多,这就造成了算法的I/O代价升高。RVLRkNN_Basic算法随着k值的逐渐增加,搜索区域中的障碍物也会增加,这也会造成I/O代价较高。对于OLRkNR算法,由于在数据集约减过程中将大量的非候选集过滤掉,又通过剪枝过程得到了更精确的候选集,因此降低了查询算法的I/O代价。 Fig.4 Effect of k on I/O cost图4 k值对I/O代价的影响 在其他条件不变的情况下,实验设定k=15,障碍物数量为1000,区域数量为5000。测试在不同数量的查询线段环境下对算法CPU时间的影响。如图5所示,这4组算法的CPU时间均随着查询线段数量增加呈上升趋势。但本文所提算法OLRkNR的上升趋势较为平缓,而其他3组算法的变化在达到一定程度时上升迅速。这是由于OLRkNR算法有效利用过滤过程和剪枝策略,提高了查询效率。而LNN_Basic算法随着查询线段增加,所要访问的区域数量也随之增加,这样浪费了大量的时间。RVLRkNN_Basic算法对查询线段集中每条线段都要搜索它的kLNR(kline nearest region),从而降低了查询效率。RkNNobs_Basic算法随着查询线段数量增加,区域重叠现象严重,这种情况会使CPU时间增加。故在其他条件相同时,只考虑对CPU时间的影响,OLRkNR算法较优。 Fig.5 Effect of query lines number on CPU time图5 查询线段数量对CPU时间的影响 进一步分析不同数量的查询线段对I/O代价的影响。如图6所示,4组算法的I/O代价呈上升趋势,OLRkNR算法上升趋势较其他3组对比算法平缓。这是因为OLRkNR算法在过滤过程筛选掉大量非候选者,降低了I/O代价。故其他条件相同时,只考虑I/O代价的影响,OLRkNR算法性能较优。 Fig.6 Effect of query lines number on I/O cost图6 查询线段数量对I/O代价的影响 Fig.7 Effect of region set size on CPU time图7 区域集规模对CPU时间的影响 图7给出了区域集规模对CPU时间的影响。实验设定k=15,查询线段数量为50,障碍物数量为1000。从图中可以看出随着区域集数量的增加,4种算法的CPU时间均呈现上升趋势,但本文提出的OLRkNR算法的上升趋势较为平缓,其余3种对比算法的变化趋势比较显著。这是由于OLRkNR算法利用了剪枝过程,缩小了查询范围,从而降低了查询时间。对于LNN_Basic算法来说,该算法需要对数据集中的每个区域进行搜索,浪费大量时间,因此它的上升趋势最为明显。故在其他条件相同时,只考虑CPU时间的影响,OLRkNR算法较优。 Fig.8 Effect of region set size on I/O cost图8 区域集规模对I/O代价的影响 在实验设定条件不变的情况下,进一步测试在不同大小的区域集环境下对算法I/O代价的影响,实验结果如图8所示。从图中可以看出OLRkNR算法的变化趋势较为缓慢,而其他3组对比算法增长变化的趋势较为明显。这是因为LNN_Basic算法中需要计算每一区域的k级最近邻,由于区域集数量越多,造成查询过程中无关数据访问量越多,从而导致I/O代价不断变大。RVLRkNN_Basic算法随着区域数量增多,障碍物的搜索数量也逐渐增多,则会造成算法I/O代价较高。RkNNobs_Basic算法可以将空间分成6等份,则在区域集数量增多的情况下,搜索区域频繁重叠的现象也会增加,使得算法I/O代价升高。因此在其他条件不变的情况下,只考虑对I/O代价的影响,OLRkNR算法更优。 接下来测试障碍物数量对算法CPU时间的影响。实验设定k=15,查询线段数量为50,区域数量为5000。实验结果如图9所示,4种算法的CPU时间随着障碍物的增加均有所增加。OLRkNR算法受障碍物数量改变的影响较小,这是因为算法中有针对障碍物剪枝过程,在查询过程中只需要考虑有效障碍物对查询的影响即可,减少查询的运行时间。 Fig.9 Effect of obstacles number on CPU time图9 障碍物数量对CPU时间的影响 改变障碍物数量测试4种算法随着障碍物数量增加I/O代价变化情况。如图10所示,3组对比算法I/O代价增幅较大。这是因为LNN_Basic算法需要对数据集中的每个区域进行搜索,浪费大量时间,所以它的上升趋势最为明显。RVLRkNN_Basic算法随着障碍物数量的增多,它所要搜索的数据就会增加,那么就会造成I/O代价升高。RkNNobs_Basic算法将数据空间分成6等份,那么随着障碍物增加,重叠区域就会增加,这样就造成I/O代价逐渐增加。故OLRkNR算法较优。 Fig.10 Effect of obstacles number on I/O cost图10 障碍物数量对I/O代价的影响 本文提出了障碍环境下的线段反k最近区域查询方法。解决了在障碍环境之下的线段到区域的近邻问题。本文的查询过程主要分为数据约减阶段、剪枝过程以及精炼过程。在数据约减过程中,结合线段Voronoi图的定义与性质,障碍环境下的线段最近区域定义以及线段障碍距离的定义,提出了针对区域集合和障碍物集合的剪枝策略,给出了相应的剪枝算法。在精炼过程中,主要针对剪枝过程后的数据候选集进行筛选,得到更为精确的查询结果,并给出了相应的精炼定理和算法。通过实验证明本文所提的算法具有较高的效率。未来研究重点集中在路网环境下的组k最近区域查询方法。3 障碍环境下线段反k最近区域查询方法
3.1 约减数据集
3.2 剪枝过程
3.3 精炼过程
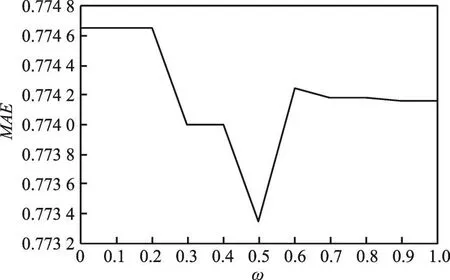

4 实验与分析






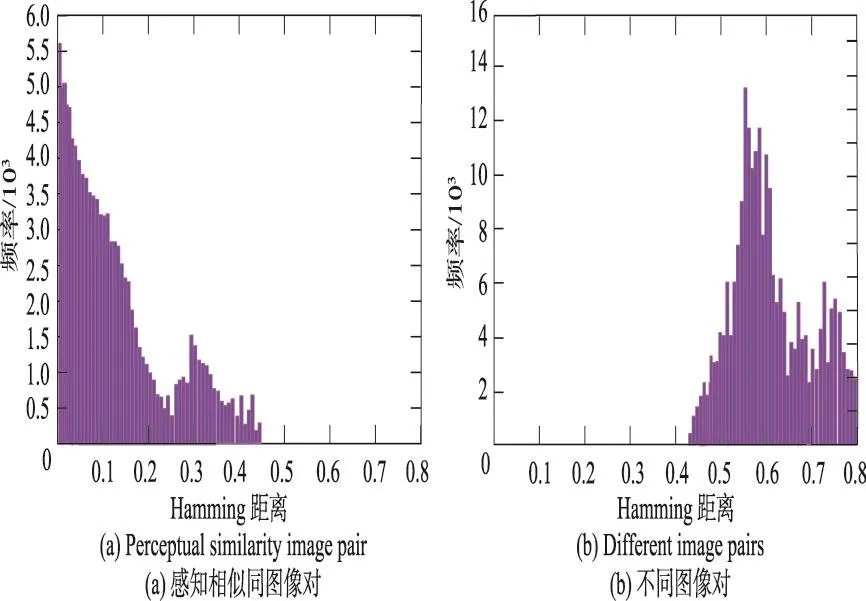

5 结束语
