互连网络的故障诊断研究综述*

郭 晨，彭 硕，王 博，肖志芳，刘 华

井冈山大学 电子与信息工程学院，江西 吉安 343009

1 引言

超大规模集成电路和晶片规模集成电路的飞速发展，推动着并行计算技术的不断进步。当前，几乎所有的自然科学都转向了精确化和计算化的道路，从而产生了一系列诸如计算物理学、计算化学、计算生物学、计算地质学、计算气象学和计算材料学等计算科学。并行计算技术的发展极大地增强了人们从事科学研究的能力，加速了科技转化为生产力的过程，深刻地改变着人类认识世界和改造世界的方法与途径。

并行计算技术是将复杂的计算任务交由一组处理器来协同完成。因此，并行计算需要一个支撑通信和数据交换的运行策略[1]。互连网络（interconnection network）就是这么一个专门服务于处理器和内存模块的通信机制[2]。现行互连网络的一个典型事例就是拥有成千上万个处理器的超级计算机系统。以2017年蝉联世界最强超级计算机TOP10第一名的神威∙太湖之光为例，它使用了40960块国产的申威26010众核处理器。在一个规模如此巨大的计算机系统的运行过程中，出现处理器故障的风险很高，而处理器故障若不能被及时诊断出并得到正确处理，将可能带来极其严重的灾难性后果。而如果超级计算机系统是按照具备一定规则的互连网络拓扑结构进行连接，通过对互连网络拓扑结构的可靠性研究，可以得出其在各种条件下的诊断度（诊断能力）。当故障处理器数目低于诊断度时，就可以根据简单的诊断算法在带电状态下进行快速的诊断，找出故障处理器的所在位置，进而进行及时的修复和更换处理。由此，引发了学界对互连网络诊断度为代表的可靠性问题的研究，其中又以系统的运行可靠性最为典型。维持系统运行可靠性的主要手段之一就是系统的故障诊断。当前，仍有部分系统还在沿用传统的故障诊断方式，通过一个所谓的“中心处理器”来测试每一个处理器的运行状态，从而给出故障评价。这种诊断方式工作量巨大并且多数情况都需要断电乃至拆解系统，既不准确又缺乏实际的操作性。因此，Preparata等人提出了一种基于图论的“系统级故障诊断”（system level diagnosis）理论[3]。系统级故障诊断充分利用了每一个处理器的处理能力，让处理器之间进行相互测试，通过综合分析来识别故障。通常情况下系统级故障诊断可以带电进行。因此，系统级故障诊断既经济又便捷，是多处理器并行计算机故障诊断的主要发展方向之一。

使用系统级故障诊断进行故障诊断的前提是要得到互连网络拓扑结构的各种诊断度性能指标。当前，规则互连网络仅有超立方网络在得到较为完整的诊断度研究之后被成功地应用到INTEL和NCUBE计算机[1]。而以超立方网络变种为代表的其他互连网络的故障诊断研究尚不系统，普遍缺乏完整的诊断度参数，这种情况势必影响到互连网络在多处理器并行计算机中的应用和推广。基于此，本文以超立方网络及其变种为代表的互连网络为研究对象，通过拓扑结构研究对以超立方网络及其变种为代表的互连网络拓扑结构的继承关系、拓扑性质、成本、连通度进行了系统分析。在此基础上，系统阐述了互连网络的故障诊断度研究现状，包括精确故障诊断度、非精确故障诊断度、条件故障诊断度、顺序故障诊断。并阐明了在互连网络上执行非精确故障诊断和顺序故障诊断是进一步提高系统诊断能力，保障运行可靠性的有效手段，以及相关研究鲜见报道的研究现状。最后指出包括互连网络拓扑结构研究、互连网络的非精确故障诊断研究和互连网络的顺序故障诊断研究在内的3个主要研究方向。本文的综述为互连网络的可靠性研究提供了较为完整的数据参数和关联体系，从而促进互连网络在多处理器并行计算机的应用和推广。

2 互连网络拓扑结构研究

互连网络几乎出现在所有涉及通信的计算机系统中。在设计一个系统的通信网络时，需要考虑从连接的物理属性到通信协议等诸多因素，而其中的首要问题是要确定连接的方式，也就是互连网络的拓扑结构[4]。互连网络的拓扑结构研究是互连网络研究的核心问题之一，它直接决定了系统的协同处理能力[1]。互连网络的拓扑结构通常采用图论表示，其中结点表示处理器，边表示处理器之间的通信连接。在选择互连网络的拓扑结构时，需要着重考量网络直径、构造成本（连接边数）和可靠性等因素。其中，网络直径是评价互连网络静态性能的主要参数之一，也是衡量并行计算速度的主要指标[5]，而构建成本通常以连接边数的形式出现，可靠性则以连通度与诊断度为主要指标，体现出系统的容错能力与诊断能力。

2.1 线性阵列和树形结构

线性阵列和树形结构被认为是最简单的并行计算机互连网络拓扑结构[6]。对于n个结点组成的线性阵列而言，它只需要n-1条边就可以连通整个网络，构造成本超低。但是，任何位置的故障就会使得线性阵列陷入瘫痪。树型结构则是一个易扩展的无环图，其中每一条边都是一条割边，任意两个结点都只有唯一的一条路径连通。因此，任何位置的故障也会使得树型结构不连通。与线性阵列类似，树型结构的构造成本也很低。由于结构都无环，线性阵列和树形结构的网络直径都等于最长路径的长度，具体数值与总结点数在同一级别，这显然过大。

2.2 超立方网络

为了降低网络直径，学者们充分利用维数空间的优点，相继提出了 Cosmic cube[7]、N-cube[8]、Binaryn-cube[9]、Booleann-cube[10]等多种类似拓扑结构。Saad等人把这类高度并发并且松散耦合的互连网络拓扑结构统称为超立方网络（hypercube，Qn）[11]。超立方网络具有规则性、对称性、网络直径小、连通性强、递归结构、可划分性和相对较小的连接复杂性等优点。基于超立方网络的并行计算机由于具有高能力的互连性和更加优秀的连通度，被认为是较为理想的并行计算机互连网络拓扑结构之一[11]。然而，超立方网络并没有充分利用好其硬件条件来有效减低网络直径[4]，从而影响到整体的并行计算速度。

同时，超立方网络的连接边会随着维数的增加成几何对数增长，这种增长对于低维超立方网络而言影响不大，但是对于高维超立方网络而言影响巨大。同时，超立方网络的结点数目被限定为2的n次方，因此超立方网络的结点规模并不能随需要进行任意的扩展[12]。基于此，后续又提出了新一代的超立方网络拓扑结构，包括广义超立方网络（generalized hypercube）[13]、不完全超立方网络（incomplete hypercube）[14]、超级立方网络（supercubes）[15]和增量可扩展超立方网络（incrementally extensible hypercube）[16]。但是这些拓扑结构不规则、不对称、结点的度也差异较大，难以取代超立方网络的地位。

2.3 扭立方网络

为了使系统具有较好的实用性，通常互连网络必须具有一定的规则性和可扩展性。一般的做法是通过让互连网络具有笛卡尔积构造性来实现[17]。其中最为极端的一个例子就是超立方网络。虽然构建简单和规则可以简化对网络直径和路由的分析，但是这将会产生太多的对称性（包括结点对称和边对称），如图1所示。通过笛卡尔积生成的超立方网络包含有太多类似的通路，由此必然造成一个不必要的较大网络直径[17]。为了减低超立方网络的网络直径，1987年，Hilbers等人根据特定规则对超立方网络的边实施“扭曲”（Twist）操作，提出了扭立方网络（twisted cube，TQn）[17]。TQn保持了超立方网络Qn原有的n正则性，整体连通度为n。如图2所示，TQ3中任意两个结点之间的最大距离是2，而图1所示的超立方网络Q3是3。因此，扭立方网络几乎降低了一半的网络直径，并且具有更好的汉密尔顿性质和嵌入性[18]。但是，扭曲操作势必破坏超立方网络的超高对称性，使得扭立方网络无法通过笛卡尔积生成[17]，从而失去结构的可划分性，并且加大了连接复杂性。

Fig.1 Topology ofQ3图1 Q3拓扑结构图

Fig.2 Topology ofTQ3图2 TQ3拓扑结构图

2.4 折叠超立方网络

为了减低网络直径，同时维系一定的对称性，1991年，El-Amawy和Latifi提出了折叠超立方网络（folded hypercube，FHn）[19]。折叠超立方网络是在超立方网络的基础上，通过增加一些额外边来降低系统的网络直径。FHn(n=3)的拓扑结构如图3所示。折叠超立方网络结点数与超立方网络一样，其网络直径却几乎只有超立方网络的一半，而边数更是比超立方网络多出2n-1条。折叠超立方网络保持了超立方网络的部分对称性，但是额外增加的2n-1条边将较大程度增加系统的构造成本，严重影响到系统的性价比。

Fig.3 Topology ofFH3图3 FH3拓扑结构图

2.5 交叉立方网络

为了减低网络直径，同时保持相对合理的对称性和性价比，1991年，Efe提出了交叉立方网络（crossed cube，CQn）[20-21]。交叉立方网络是在超立方网络的基础上，通过关联对[20]的对应关系“交叉”部分边而形成的一种互连网络拓扑结构。交叉立方网络继承了超立方网络的规则性、递归结构、可划分性、强连通性的特点，拥有和超立方网络一样的结点数、边数和连通度[20,22-23]。如图4所示，CQ3中结点之间的最大距离为2，同样低于超立方网络Q3的3。因此，交叉立方网络以牺牲超立方网络的超高对称性为代价，缩小了几乎一半的网络直径，并且表现出很强的嵌入性。

Fig.4 Topology ofCQ3图4 CQ3拓扑结构图

交叉立方网络CQn与扭立方网络TQn相比，在结点数、边数、网络直径和连通度等多方面都具有相同的取值。但CQn具有在故障结点存在的条件下的哈密尔顿特性，该性质TQn不具备。同时TQn的扭曲操作具有双向性，而CQn的关联对交叉操作仅仅会使得最左边的不同取值地址位和偶数地址位发生变化，这就会影响到特定结点间的连通，从而带来了一定程度的不确定性，影响到系统的稳定性[24]。

2.6 莫比乌斯立方网络

“扭曲”和“交叉”等操作势必降低互连网络的动态性能，从而影响系统的信息交互能力。为了平衡互连网络拓扑结构的静态性能和动态性能，1995年，Cull等人提出了莫比乌斯立方网络（Möbius cube，MQn)[1]。MQn(n=3)的拓扑结构如图5所示。莫比乌斯立方网络与超立方网络一样，具有相同的结点数、边数和结点的度。莫比乌斯立方网络的网络直径也几乎只有超立方网络的一半，结点间的平均步数只有超立方网络的2/3，表现出优于超立方网络的动态性能[1]。此外，莫比乌斯立方网络还具有超立方网络不具有的汉密尔顿性质和嵌入性[25]。但是，莫比乌斯立方网络不具有超立方网络的超高对称性。各种算法都是基于特定结点或边，复杂度也相对较高。

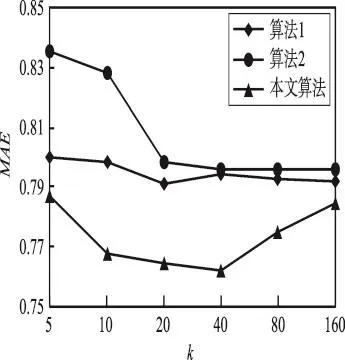
Fig.5 Topology ofMQ3图5 MQ3拓扑结构图

2.7 平衡立方网络

超立方网络及其前期的大多数变种都普遍关注于缩小网络直径和信息交换两方面[26]。而随着处理器规模的不断扩大，系统发生故障的可能性也成倍乃至成几何倍数增加，因此互连网络的设计需要充分考虑拓扑结构的容错能力。基于此，1992年，Wu和Huang提出了平衡立方网络（balanced hypercube，BHn）[27]，BHn(n=3)的拓扑结构如图6所示。平衡立方网络在继承超立方网络的强连通性、规则性和对称性的同时，还具有特殊的负载均衡能力，使得它具备即时容错能力。具体表示为当故障处理器发生故障后，其任务可以及时地在备份处理器中即时恢复。因此，平衡立方网络在不改变任务间邻接关系的基础上，支持有效的重构。此外，平衡立方网络相比超立方网络也有更低的网络直径。但是其结点数、边数都远大于超立方网络，构建成本较高，性价比较低[27]。

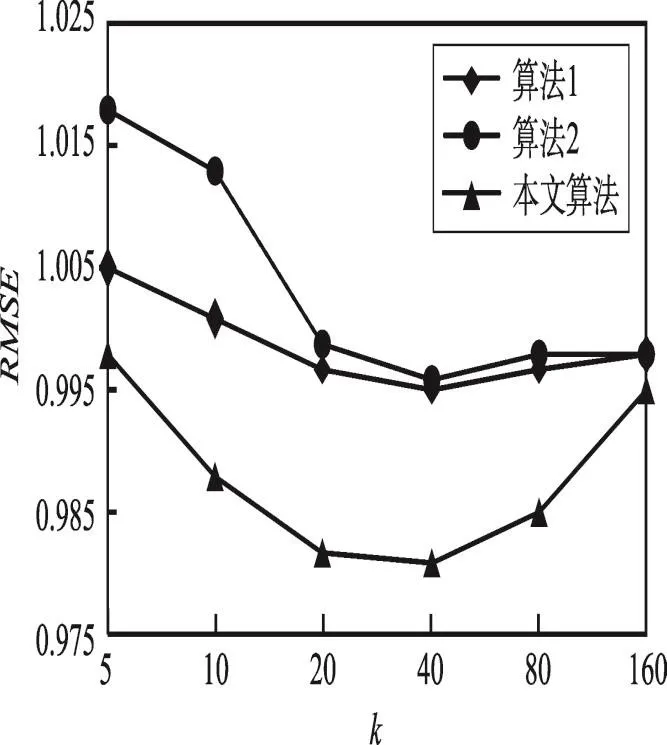
Fig.6 Topology ofBH3图6 BH3拓扑结构图

2.8 增广立方网络

扭立方网络、折叠超立方网络和交叉立方网络都以牺牲超立方网络的超高对称性为代价来减低网络直径，其实用性颇有争议[28]。为了保持较高对称性，2002年，Choudum和Sunitha提出了增广立方网络（augmented cubes，AQn)[28]，AQn(n=3)的拓扑结构如图7所示。增广立方网络是超立方网络的一个加强网络，它不仅保持了超立方网络的良好拓扑性质，并且在网络直径、嵌入性等方面拥有更好的属性。但是在硬件成本和连通度上却付出了较大的代价，其边数和连通度都几乎是超立方网络的2倍。

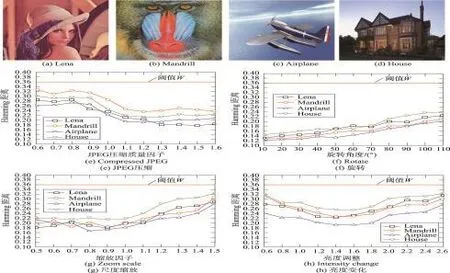
Fig.7 Topology ofAQ3图7 AQ3拓扑结构图

2.9 交换超立方网络

随着维数的增加，超立方网络及其多数变种，如扭立方网络、交叉立方网络、莫比乌斯立方网络等，其连接边的增加远比结点的增加要快，而且这种差异会越拉越大。更为严重的是，连接边数以及复杂度直接与硬件成本和集成电路的实现效果相关联[29]。而单纯的缩小连接复杂度会严重损害到系统的性能、应用支持、连通度、路由和可靠性等多个方面[29]。因此简单地缩小连接复杂度难以有效地提高性价比，而在拓扑结构上新的创新才是研究的方向。基于此，2005年，Loh等人通过移除超立方网络的一些连接边，提出了交换超立方网络（exchanged hypercube，EH(s,t)）[29]，EH(s,t)(s=1,t=2)的拓扑结构如图8所示。交换超立方网络在连接边几乎只有超立方网络一半的情况下保持了与超立方网络相似的网络直径，同时还继承了超立方网络的偶泛圈性和强连通度等特点。交换超立方网络包含有两个参数，这也使得互连更加灵活。

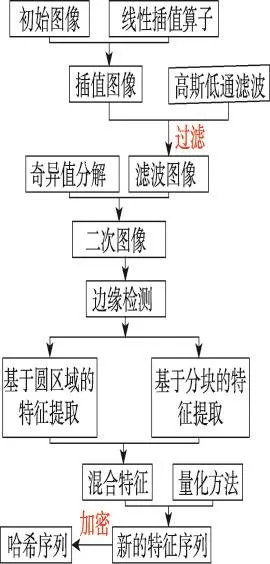
Fig.8 Topology ofEH(1,2)图8 EH(1,2)拓扑结构图

2.10 超立方网络二次变种拓扑结构

近年来，互连网络拓扑结构研究进入了新的阶段，出现了一些超立方网络的二次变种，包括：2002年Zhang提出的折叠交叉超立方网络（folded-crossed hypercube，FCHn）[30]，2005年Yang等人提出的局部扭立方网络（locally twisted cubes，LTQn）[31]，2013年Li等人提出的交换交叉立方网络（exchanged crossed cube，ECQ(s,t)）[32]以及Peng等人提出的折叠局部扭立方网络（folded locally twisted cubes，FLTQn）[33]。

3 互连网络的故障诊断与诊断度研究

互连网络定义了并行计算机中各处理器之间的互连关系，而互连关系又影响到并行计算机的协同性能和构建成本。几种主要互连网络拓扑结构的拓扑参数如表1所示。迄今为止，超立方网络及其变种的实际应用还很少，影响超立方网络及其变种应用和推广的主要原因之一是其可靠性研究尚不系统，其中又以故障诊断度研究最为突出。互连网络的故障诊断是支撑互连网络运行可靠性的主要指标之一，需要展开系统研究。

多处理器并行计算机系统的故障诊断分为逻辑电路级别和系统级[44]。由于包含了大量的互连单元，所以多处理器并行计算机的故障诊断解决方案应该倾向于系统级别，而不是逻辑电路级别。系统级故障诊断充分利用了多处理器并行计算机中每一个处理器的测试能力，让处理器之间进行相互测试，通过诊断算法对测试结果进行综合分析来识别出故障结点的所在。因此，系统级故障诊断理论实现了多处理器并行计算机故障诊断的自我诊断以及用户透明重构与恢复[45]，是多处理器并行计算机故障诊断的主要研究方向之一。

Table 1 Topological parameters of several main interconnection networks表1 几种主要互连网络拓扑结构的拓扑参数

经历了半个世纪的研究与发展，迄今为止，系统级故障诊断已经提出了一系列故障诊断理论，具体包括：t-可诊断[3]、t/s-可诊断[46]、t1/t1-可诊断[47]、t/k-可诊断[48]、条件t-可诊断[49]、g正确邻结点条件t-可诊断[50]和条件(t,k)-可诊断[51]。根据诊断特征的不同可归纳为3种类型，分别为：精确故障诊断、非精确故障诊断和条件故障诊断，如表2所示。同时，t-可诊断和t/k-可诊断又可进一步分为一步故障诊断和顺序故障诊断两种具体形式。因此，故障诊断理论也可以根据诊断迭代次数的不同归属为一步故障诊断和顺序故障诊断两种范畴。

传统的t-可诊断对故障结点没有任何限制，诊断精确而全面，因此被称为精确故障诊断。非精确故障诊断全面而不精确（允许小部分正常结点被误诊断）。条件故障诊断限制一些低概率情况的发生。间歇性故障诊断面对的是间歇性故障。其中顺序t-可诊断[3]、(t,k)-可诊断[52]、顺序t/k-可诊断[53]和条件(t,k)-可诊断属于顺序故障诊断范畴。每一种故障诊断理论都具有各自不同的适用性和使用范围，发展的过程体现出诊断能力和诊断效果的不断进步，同时也会伴随着一定的负面效果和诊断代价。

系统级故障诊断的执行还依赖特定的诊断模型（diagnosis model）。当前主要的诊断模型有Preparata Metze Chien（PMC）模型[3]和Maeng Malek（MM）模型（包括MM*模型）[54]。PMC模型中，每一个处理器都可以测试它的邻接处理器，并且对它们的状态进行评价。但是研究发现，要直接评价处理器的故障与否有时候非常复杂，且容易出现一定程度的误判断，而通过比较的方式来界定测试结果相比直接评价要简单很多[48]。基于这种考虑，MM模型通过一个比较器把测试任务发给与它相邻的两个处理器，然后比较它们的测试结果来进行诊断。MM模型也被称为比较故障诊断模型[54]。1992年，Sengupta等人进一步提出一种特殊的MM模型——MM*模型[55]。MM*模型要求每一个处理器都必须对它的任意两个邻接处理器进行测试。PMC模型和MM模型是使用广泛的两种诊断模型，二者各具特色。

接下来，就超立方网络及其变种为代表的互连网络故障诊断研究现状进行详细说明。

3.1 互连网络的精确故障诊断与诊断度研究

1967年，Preparata等人将图论方法应用于多处理器计算机系统的故障诊断，创造性地提出了t-可诊断理论[3]。t-可诊断指的是当故障结点数目不超过t时，所有故障都可以被诊断出来。t-可诊断又可以进一步分为一步t-可诊断和顺序t-可诊断两种类型。其中顺序t-可诊断将在后续顺序故障诊断中详细说明。一步t-可诊断指的是当系统的故障结点数不超过t时，可以一步找出所有的故障结点。一步t-可诊断的诊断能力（诊断度）与点连通度关系密切[56]。但是，如表3所示，一步t-可诊断的诊断能力很小，甚至可以忽略，而难以发挥出实际的诊断作用。以n维超立方网络为例，它的诊断度为n[57-58]，与总结点数的占比仅为n/2n，当n≥10时n/2n<1%。

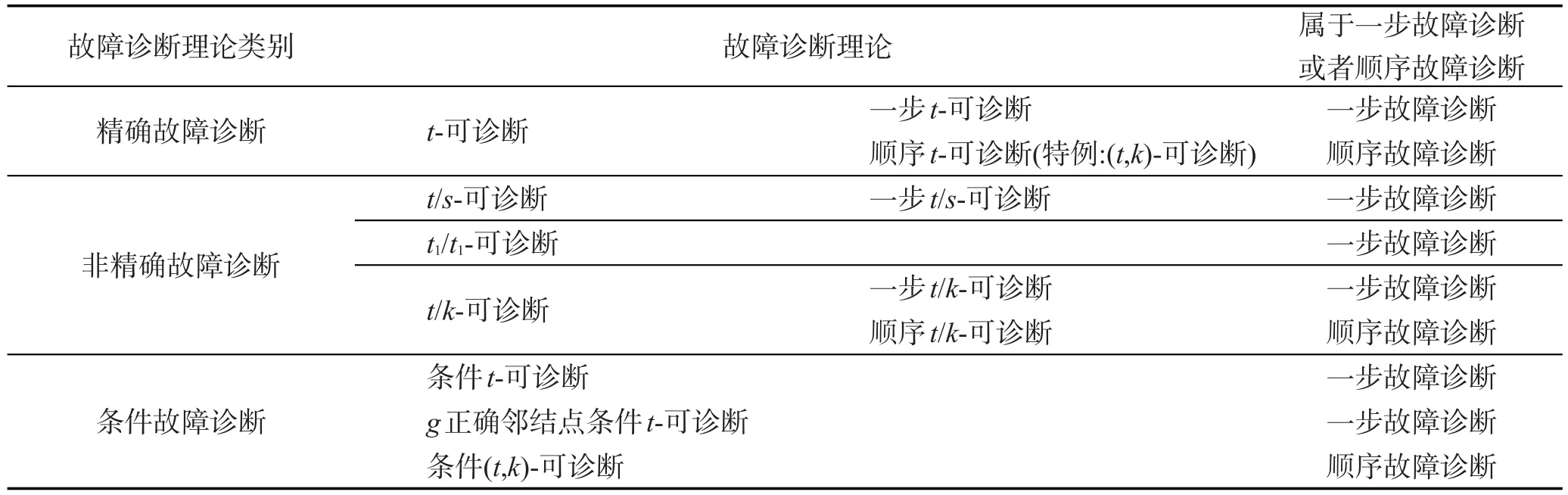
Table 2 Classification of fault diagnosis theory表2 故障诊断理论分类

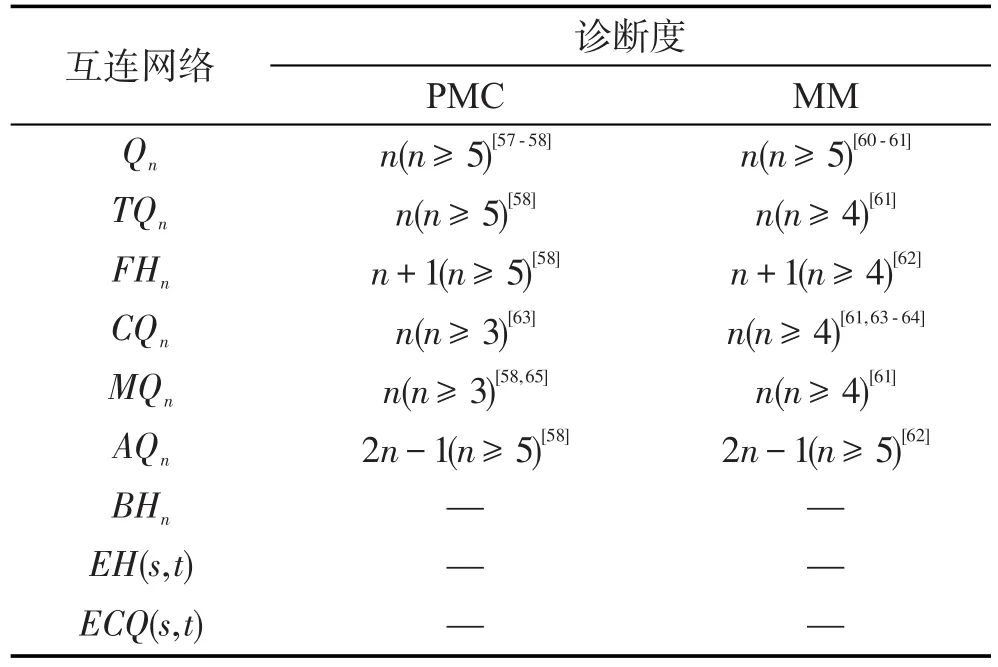
Table 3 Precise diagnosabilities of several main interconnection networks表3 主要互连网络的精确故障诊断度

3.2 互连网络的非精确故障诊断与非精确诊断度研究

为了提高系统的诊断能力，1975年Friedman以牺牲诊断的部分精确性为代价提出了一种新的故障诊断理论——t/s-可诊断[46]，t/s-可诊断在确保故障被全部诊断的同时允许出现小部分的误诊断（正常处理器被误诊断为故障处理器），是一种非精确的故障诊断理论。t/s-可诊断表示当故障结点数目不超过t时，所有的故障结点可以被圈定在一个大小不超过s的结点集合中。t/s-可诊断有误诊断略高的缺点，最坏情况下误诊断数可达s-1。t/s-可诊断的性质也很难获取，即使s=n-1研究难度依然巨大[59]。因此，严重制约了t/s-可诊断的研究和发展。而当t=s时，研究难度略微舒缓，此时的t/s-可诊断表现出诸多的性能优势，这就是t/s-可诊断的典型特例——t1/t1-可诊断[47]。

t1/t1-可诊断是1978年Kavianpour等人提出的一种故障诊断理论[47]。t1/t1-可诊断要求在故障结点数目不超过t1的情况下，所有的故障结点可以被圈定在一个大小不超过t1的结点集合中。t1/t1-可诊断也被称为悲观故障诊断。之后，Kavianpour等人进一步证明同等诊断能力的t1/t1-可诊断系统，相比t-可诊断系统而言，可节省一半的测试边[47]。1981年Chwa等人给出了t1/t1-可诊断的充要条件，并且指出t1/t1-可诊断至多只有一个被误诊断的结点[59]。t1/t1-可诊断是t/s-可诊断的一种特例，相比t/s-可诊断，t1/t1-可诊断可以有效降低误诊断率。

由于t/s-可诊断中允许存在着较大比例的误诊断结点，并且这种故障诊断理论难以控制被误诊断的结点数，特别是当故障集合只是一个结点时，它的误诊断比例显然不可接受。基于此，1996年Somani等人提出了t/k-可诊断[48]。t/k-可诊断认为当系统的故障集合F满足|F|≤t时，根据症候可将系统的所有故障结点圈定到结点集合F1中，F1至多有k个被误诊断的结点，即|F1|≤|F|+k。t/k-可诊断也可分为一步t/k-可诊断和顺序t/k-可诊断两种类型，其中顺序t/k-可诊断也将在后续顺序故障诊断中说明。t/k-可诊断是非精确故障诊断中一种可以控制误诊断数目并且有效提高诊断能力的故障诊断理论。

如表4所示，互连网络的非精确故障诊断度大幅度提高了系统的诊断能力，但是由于研究难度较大，其中绝大多数诊断度未被求得。

3.3 互连网络的条件故障诊断与条件诊断度研究

条件t-可诊断是2005年Lai等人提出的一种限定条件的故障诊断理论[49]。条件t-可诊断要求系统中的每一个结点至少有1个正确（未发生故障）的邻结点。但是对于一个维数较大的互连网络而言，只是要求每一个结点至少有1个正确邻结点的设定条件相对保守。基于此，2012年Peng等人提出另一种限定条件的故障诊断理论——g正确邻结点条件t-可诊断[50]。g正确邻结点条件t-可诊断要求每一个正确的结点至少有g个正确的邻结点。通常情况下，g正确邻结点条件t-可诊断的诊断度是条件t-可诊断的数倍[76]，但是g如何合理取值业内没有定论，也缺乏依据。

条件故障诊断是以牺牲故障发生的小概率事件为代价，成倍提高系统诊断能力的一种故障诊断理论。但是，这种牺牲势必造成故障诊断的局限性。同时，诊断能力的提升也较为有限。以n维超立方网络为例，它在PMC模型下的条件诊断度为4n-7[36,49,77]，与总结点数的占比为(4n-7)/2n，当n≥10时(4n-7)/2n<3.3%，仍然很小。迄今为止，如表5所示，互连网络的条件故障诊断度基本都已求出，而g正确邻结点条件诊断度却仍有大部分未被求出。

Table 4 Inaccurate diagnosabilities of several main interconnection networks表4 主要互连网络的非精确故障诊断度

3.4 互连网络的顺序故障诊断与顺序诊断度研究

顺序故障诊断是一种采取多步迭代进行难度分散的故障诊断理论。其中顺序t-可诊断是通过反复迭代的方式来诊断系统的故障集合，每一次迭代至少要有一个新的故障结点被确认，这个被确认的故障结点子集会在下一次迭代开始之前被维修和替换，迭代会一直持续下去，直到所有的故障结点被确认并被维修替换为止[3]。和顺序t-可诊断类似，顺序t/k-可诊断要求在故障结点数不超过t的情况下，允许迭代过程中出现误诊断，要求总的误诊断数不能超过k个[53]。根据顺序t-可诊断的定义可知，最坏情况下，顺序t-可诊断的每一次迭代都只能确定一个故障结点的所在，因此整体的迭代过程可能需要一定的时间，这就可能降低诊断的实时性。基于此，2003年，Araki等人提出了新一代的顺序t-可诊断理论——(t,k)-可诊断[52]。(t,k)-可诊断要求在故障结点数不超过t时，每次迭代至少可以确定k个故障结点，其中k≤t。(t,k)-可诊断最坏情况下的最大迭代次数仅为ét/kù，比顺序t-可诊断的最大迭代次数t要小很多。因此，(t,k)-可诊断改善了顺序t-可诊断的过度延时，是顺序故障诊断的发展方向。

事实上很多故障诊断理论都存在故障随机分布和故障条件分布两种情景[51]，(t,k)-可诊断也不例外。在故障随机分布的情况下k=t时的(t,k)-可诊断就是传统的一步t-可诊断，k=1时的(t,k)-可诊断就是顺序t-可诊断。而当故障结点不是随机分布，而是和条件t-可诊断一样，要求所有的结点都遵循至少有一个正确的邻结点。这种情况下的(t,k)-可诊断称为条件(t,k)-可诊断[51]。条件(t,k)-可诊断充分融合了条件t-可诊断和(t,k)-可诊断的优点，在有效利用测试资源的基础上提高了系统的诊断能力。

（2）拓宽目的层频带，即特殊处理过程。将目的层地震资料做小波变换，在小波域进行信号重构，保障提高地震分辨率的同时，还保留了地震资料很好的保真度。

Table 5 Conditional diagnosabilities of several main interconnection networks表5 主要互连网络的条件诊断度

如表6和表7所示，迄今为止，互连网络的顺序故障诊断度多数未被求出。

基于上述分析，互连网络的精确故障诊断精确，但是诊断能力差。互连网络的条件故障诊断能力有所提高，但是提高程度有限，且条件故障诊断忽略的小概率事件现实情况下时有发生。因此，在互连网络上执行非精确故障诊断和顺序故障诊断是进一步提高系统诊断能力，保障运行可靠性的有效手段。然而，如表4、表6和表7所示，相关研究鲜见报道，研究成果也较为零星。

4 互连网络的故障诊断研究展望

根据互连网络故障诊断的研究现状，接下来对未来的研究方向进行展望，具体包括互连网络的拓扑结构研究、互连网络的非精确故障诊断研究和互连网络的顺序故障诊断研究三方面。

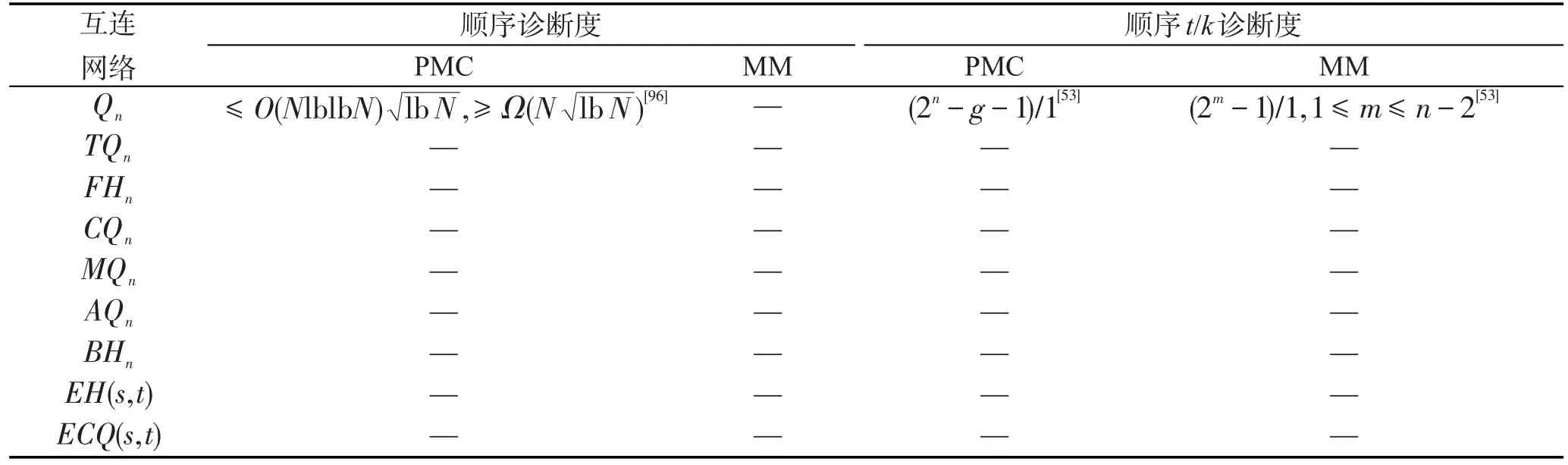
Table 6 Sequential diagnosabilities of several main interconnection networks(1)表6 主要互连网络的顺序故障诊断度（1）

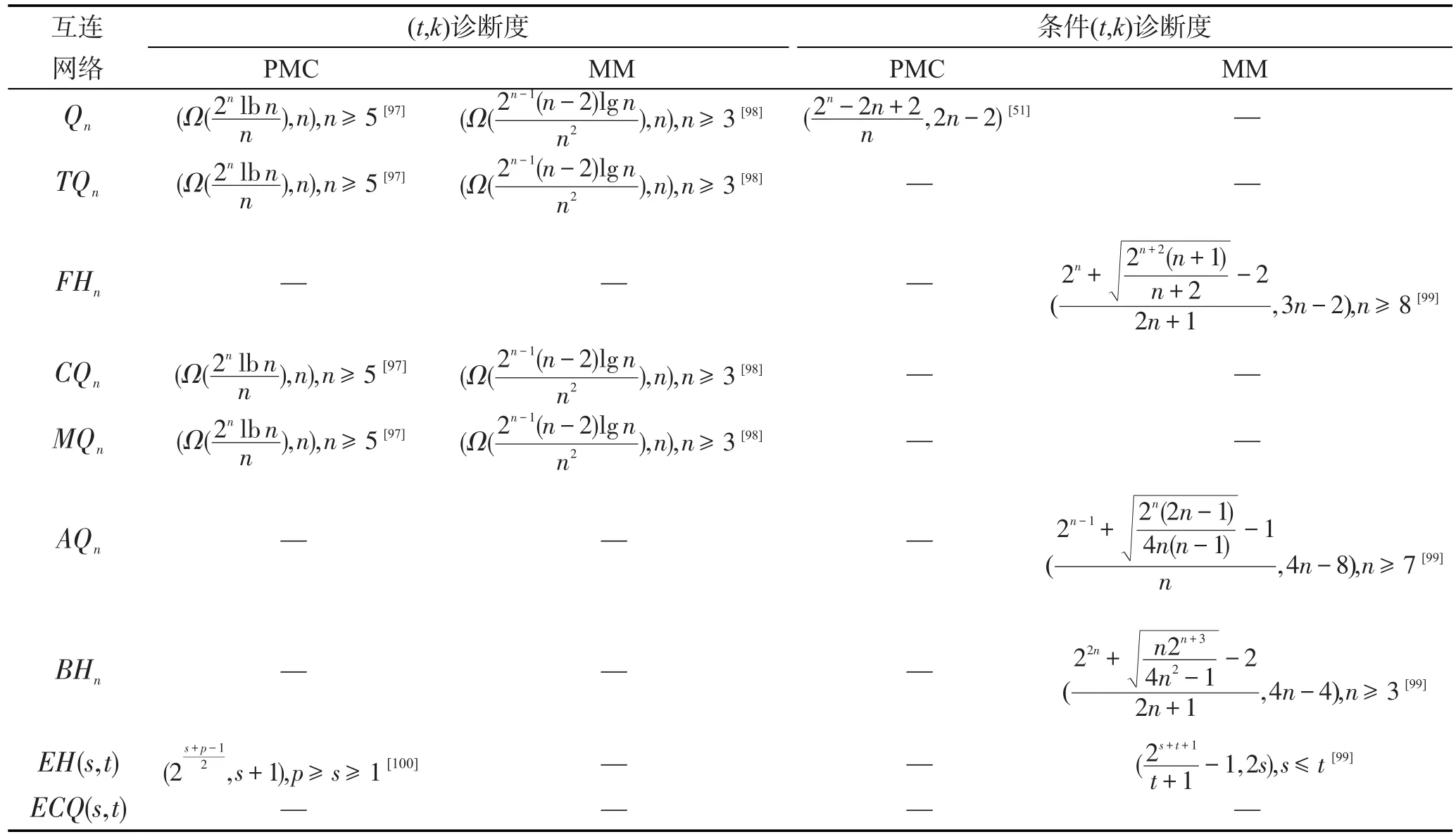
Table 7 Sequential diagnosabilities of several main interconnection networks(2)表7 主要互连网络的顺序故障诊断度（2）

4.1 互连网络的拓扑结构研究

由互连网络拓扑结构的研究现状可知，要设计一个各个方面表现都最优的互连网络几乎不可能。因此，实际应用中就需要根据具体的需求进行必要的妥协，特别是在性能和成本之间进行合理的权衡，选择出一个符合当前实际需要的互连网络拓扑结构。由于需求的多面性，客观上经常要求使用的互连网络需同时具有几种现有互连网络拓扑结构的优点。因此，互连网络的二次变种甚至多次变种将成为后续互连网络拓扑结构研究的主要方向之一。通过二次或者多次变种，可以使得新生成的互连网络拓扑结构同时继承两种或者多种互连网络拓扑结构的优点，进而最大程度地发挥出综合的性能优势，以提供更为适用的互连网络拓扑结构。

4.2 互连网络的非精确故障诊断研究

如表4所示，互连网络的非精确故障诊断度大幅度提高了系统的诊断能力。但是由于研究难度较大，其中绝大多数诊断度未被求得，主要原因在于缺乏非精确故障诊断的关键性特征。然而，Ye等人在研究超立方网络、交叉立方网络、莫比乌斯立方网络等互连网络时发现，这些互连网络在满足非精确故障诊断时，存在着一个结点规模超过总结点数一半的巨大连通分支[101-102]，这个连通分支富含众多性质特征，比如：连通分支内的结点状态值相同，连通分支和允许故障集合（allowable fault set）[3]以外的结点数不超过2个。如果以这个连通分支为抓手，借助“集团”的概念和性质定理[103]，可以进一步确定与这个连通分支所在的集团相邻的集团都是故障集团，所包含的结点都是故障结点[104]。进而，在充分研究集团性质和各类连通度的基础上，极有可能提炼出非精确故障诊断的关键性特征，进而展开互连网络的非精确故障诊断度研究。因此，互连网络的非精确故障诊断研究存在着重新展开的有利条件。利用可区分性的充要条件和允许故障集合的性质特征构建起非精确故障诊断的关键性特征。最后，结合具体的互连网络拓扑结构，以相关拓扑性质和非精确故障诊断的关键性特征为基础，求出互连网络非精确故障诊断度的取值上限和下限，并通过仿真实验验证相关结论。因此，互连网络的非精确故障诊断研究是一个值得广泛关注的研究方向。

4.3 互连网络的顺序故障诊断研究

如表6和表7所示，互连网络的顺序故障诊断度可以有效地提高系统的诊断能力。但是，需要牺牲一定的时间复杂度，这对于诊断的及时性有一定影响，但是在当前的处理能力下这点影响并不明显。同样，互连网络顺序故障诊断度的研究也存在着较大难度。然而，在(t,k)-可诊断时发现，其诊断度与P(t)[92]、Q(t)[92]、Dˉ(σ)[92]、φ(x1)[97]、ϕ(x1,x2)[97]和I(m)[97]等特定函数密切相关，而这些特定函数又与互连网络的相关拓扑性质密切关联。因此，在得到互连网络相关拓扑性质的基础上，结合顺序故障诊断的关键性特征，再借助系列特定函数，极有可能求出互连网络的顺序故障诊断度。

同时，到目前为止，只有t-可诊断和t/k-可诊断进一步分成了一步故障诊断和顺序故障诊断两种类型。但是就定义而言，顺序故障诊断的多步迭代也同样适用于t/s-可诊断、t1/t1-可诊断、条件t-可诊断和g正确邻结点条件t-可诊断。因此，顺序故障诊断理论存在着进一步拓展的可能。

因此，互连网络顺序故障诊断研究也是一个颇具潜力的研究方向。

5 总结

本文以提高多处理器并行计算机的运行可靠性为目标，系统梳理了互连网络的拓扑性质、互连网络的精确故障诊断度、互连网络的非精确故障诊断度、互连网络的条件故障诊断度和互连网络的顺序故障诊断度等研究成果。进而在比较分析的基础上，提出互连网络故障诊断研究的3个重要发展方向。本文的研究有助于促进互连网络在多处理器并行计算机系统的应用和推广。