一种有效的基于GraphX的分布式结构化图聚类算法*
2018-10-12时生乐赵宇海王国仁
时生乐,赵宇海,李 源,印 莹,王国仁
东北大学 计算机科学与工程学院,沈阳 110819
1 引言
图模型强大的表达能力,使其在社交、化学、生物等领域有着广泛的应用,例如在社交领域,使用图模型进行建模,将数据用一个图来表示,图中的顶点表示个体,边表示个体与个体之间的关系。随着图应用的不断增长,人们对图数据分析和管理中的基本问题进行了大量研究,其中发现聚类或社区结构是图数据分析中最重要的任务之一,通过发现数据中潜在的结构,人们可以从海量数据中提炼出有价值的信息。例如在社交网络中,通过对社交网络进行聚类分析,可以找到网络中的社区,进而可以分析社区中人们的行为并向对该社区感兴趣的人推荐社区。
在当前文献中,已经提出各种各样的图聚类算法,例如基于模块性的图聚类算法[1]、k-core算法[2]、kedge算法[3]、k-truss算法[4]、谱聚类算法[5]和局部密集子图发现算法[6]等。然而上面这些算法都不能区分一个图中顶点的不同角色,而对图中顶点的角色进行区分在现实中有重要应用。为了能够区分图中顶点的不同角色,Xu等人第一次提出结构化图聚类算法[7]。该算法使用图中顶点之间公共邻居作为聚类条件对图进行聚类,并且同时将图中的顶点分为聚类中的点、中心点、离群点3类。其中,聚类中的点指算法找出的每个簇中的顶点,中心点指横跨两个及两个以上聚类的顶点,离群点指除聚类中的顶点和中心点之外的其他顶点。例如在图1中,通过结构化图聚类算法找到图中的两个聚类:由顶点v1~v8组成的聚类1,顶点v10~v15组成的聚类2(分别用虚线圈出);同时也找到了连接聚类1和聚类2的中心点v9和离群点v16、v17、v18。
结构化图聚类在实际生活中有重要应用。例如,如果将图1看作用于传染疾病防控的图数据,图中的每个顶点表示一个人,顶点之间的连线代表人与人之间的接触关系。在传染疾病爆发时,如果能够找到连接群体之间的关键人物(例如顶点v9),并对其隔离,就能够有效阻止传染疾病在群体之间进行传播,对疾病的防控具有重要意义。
Fig.1 Structural graph clustering图1 结构化图聚类
本文通过对结构化图聚类中顶点间相似性定义和基于Hadoop[8]的MapReduce分布式结构化图聚类算法进行分析,提出一种基于GraphX[9]的分布式结构化图聚类算法。
本文主要贡献如下:
(1)通过对结构化相似性定义的分析,找到一种减少图中顶点之间结构化相似性计算数量的削减策略;
(2)通过对结构化相似性计算过程的分析,提出一种通过非精确计算顶点之间相似性来确定顶点之间是否相似的方法;
(3)通过发现现有分布式结构化图聚类算法在计算过程中需要大量磁盘I/O开销的不足,提出一种基于GraphX的结构化图聚类算法消除计算过程中的磁盘I/O开销。
本文剩余部分组织如下:第2章阐述和分析了分布式图聚类的相关工作;第3章对分布式结构化图聚类问题和相关概念进行定义;第4章详细阐述本文提出的基于GraphX的结构化图聚类算法;第5章通过对比实验分析算法的效率和可扩展性;第6章对全文进行总结。
2 相关工作
近年来,随着社交网络、生物、医学等领域的快速发展,产生大量大规模图数据集,由于内存限制,使得传统基于单机的图聚类算法[1,7,10]已经不能够处理这些大规模图数据集,因此基于分布式的图聚类算法不断出现。
分布式的图聚类算法[11-12]主要思想是将图数据集按照一定规则分布到集群的各个结点上,然后在各个结点处理一部分数据集,在计算过程中只涉及结点间的网络通信,不需要磁盘I/O开销,且可以根据数据集的规模任意添加机器,可扩展性好,理论上可以处理任意规模的数据集。因此开发分布式的图聚类算法是图挖掘研究的重点之一。
由于结构化图聚类算法能够识别出顶点的不同角色,因此在图分析中扮演着重要角色,文献[13]是目前最具代表性的图聚类算法之一,但是该算法存在大量磁盘I/O开销和大量精确计算顶点之间结构化相似性等问题。
随着分布式计算技术的快速发展,目前已经出现了以Hadoop[8]和Spark[14]为代表的分布式系统,并在商业和研究中得到广泛应用。Hadoop具有高可靠、高扩展、高容错等优点,是目前商业领域使用最多的分布式系统之一。但Hadoop也有磁盘I/O开销大、对图计算和迭代计算支持不好等缺点。Spark是一个开源的分布式内存计算框架,GraphX是Spark上的一个专门用来进行图计算的弹性分布式图系统。GraphX通过Spark将数据并行和图并行有效结合起来,极大提高了图计算的存储和执行效率,且GraphX中内置许多对图进行计算的原子操作,极大地方便图计算应用程序的开发。和Hadoop相比,Spark对迭代计算和图计算的支持更加好,而在图计算中像kcore、PageRank[15]等许多算法都需要迭代计算,这使得基于GraphX实现的图算法执行效率将会得到极大提升。
3 问题描述
3.1 相关定义
本研究主要聚焦于无向无权重图G=(V,E),其中V表示图G中所有顶点的集合,E表示图G中所有边的集合,用|V|=n表示图中顶点个数,|E|=m表示图中边的条数,(v,w)∈E表示两个端点为v和w的边,Nv、Nw分别表示顶点v和w邻居顶点的集合。
定义1(结构化邻居)对于图G中任意一个顶点v∈V,顶点v的结构化邻居定义为:H[v]={w|(v,w)∈E}⋃{v}。
例如,在图2中顶点v6的结构化邻居为H[v6]={v4,v5,v6,v7,v8,v11},顶点v7的结构化邻居为H[v7]={v6,v7,v8,v9,v10,v11}。
Fig.2 Simple example图2 一个简单示例
定义2(结构化相似性)对于图G中任意两个顶点v,w∈V,顶点v、w的结构化相似性定义为:
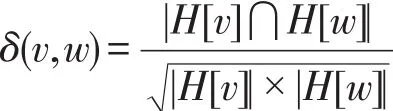
其中,|H[v]|、|H[w]|分别表示顶点v和w的结构化邻居的个数。
例如在图2中,顶点v6和顶点v7的结构化相似性为:
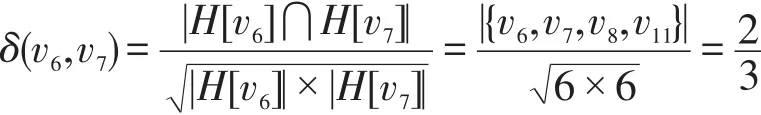
给定一个相似性阈值ε(0<ε≤1),如果顶点v和顶点w的相似性阈值δ(v,w)≥ε,则称顶点v和顶点w是相似的。例如在图2中,设定相似性阈值为ε=0.8,顶点v6和v7相似性为δ(v6,v7)=2/3=0.667<0.8,因此顶点v5和v6不相似;顶点v4和v5相似性为δ(v4,,因此顶点v4和v5相似。
3.2 基于MapReduce的算法
现有分布式结构化图聚类算法[13](parallel structural clustering algorithm for big networks,PSCAN)的主要思想是给定一个用邻接列表表示的无向、无权重图和一个相似性阈值ε(0<ε≤1),返回图中所有的聚类;该算法首先根据顶点的邻接列表计算图中所有邻接顶点对之间的结构化相似性,然后去掉图中相似性小于给定阈值ε的顶点对之间的边,最后找到图中所有的连通分量,每个连通分量就是所要找的聚类,具体算法如算法1所示。
算法1PSCAN算法
输入:一个由邻接列表表示的图G(V,E),一个相似性阈值ε(0<ε≤ 1)。
输出:图G中所有聚类的集合。
1.Mapper阶段:
2.for图中每个顶点v∈Vdo
3.for顶点v的每个邻居顶点vido
4. ifID(v) 5. 取(ID(v),ID(vi))作为key; 6. else 7. 取(ID(vi),ID(v))作为key; 8. end if; 9. 取顶点v的邻居Nv作为value; 10. 发送键值对(key,value); 11.end for; 12.end for; 13.Reducer阶段: 14.得到从Mapper阶段发送的键值对; 15.for每一个key相同的两个键值对do 16.计算这两个顶点的相似性e; 17.end for; 18.for图中的每条边(v,w)do 19.if顶点v、w的相似性e<εthen 20. 移除边(v,w); 21.end if; 22.end for; 23.计算连通分量; PSCAN算法伪代码如算法1所示,在Mapper阶段(行1~12),计算每个顶点和它们的每个邻居组成的键值对,使用ID(v)、ID(vi)的升序作为key(行4~8),使用顶点v的邻居作为value;在Reducer阶段(行13~22),计算每条边(v,w)两个端点的相似性e,如果e<ε(说明两个顶点不相似),移除边(v,w)(行19~21),最后计算图中的连通分量(行23)。算法使用标记传播算法来求连通分量,求得连通分量的集合就是最终的聚类结果。 上面算法产生大量的磁盘I/O开销,且算法需要精确计算图中所有邻接顶点对之间的相似性,降低了算法的执行效率。该算法除了执行效率较低外,存在的另一个问题是算法不能够去掉只有少量顶点组成的聚类(例如有少量顶点组成的clique[16]),因为只有少量顶点组成的聚类在图分析中没有什么意义,所以这样的聚类不应包含在最终结果中。例如在图1中,使用该算法将找到聚类1、聚类2和由顶点v17和顶点v18组成的聚类,因为根据相似性定义可知,只有两个顶点组成的聚类顶点之间的相似性恒为1,所以无论ε值为多大,只有两个顶点组成的聚类始终包含在最终结果中,降低了算法的准确性。 针对第3章PSCAN算法存在产生大量I/O开销等不足,本文提出一种基于GraphX的分布式结构化图聚类算法GXDSGC(GraphX-based distributed structural graph clustering algorithm),该算法能够很好解决上述问题。给定一个无向无权重图、一个相似性阈值ε(0<ε≤1)和聚类中顶点的最小个数minNum,GXDSGC算法找到图中所有聚类和由中心点和离群点组成的顶点的集合。下面介绍算法中用到的两个削减规则。 在现有的PSCAN算法中是计算图中所有边所关联的顶点之间的相似性,顶点之间相似性的计算在整个算法中是一个比较耗时的操作,如果能够减少图中顶点之间相似性的计算量就会大大增加算法的执行效率。通过对顶点之间相似性定义进行分析后,得到下面的削减规则。 引理1对于一个给定的相似性阈值ε(0<ε≤1)和两个顶点v和w,如果|Η[v]|<|Η[w]|×ε2或|Η[w]|<|Η[v]|×ε2,那么顶点v和w不相似。 证明因为|Η[v]|<|Η[w]|×ε2,所以 即δ(v,w)<ε,所以顶点v和w不相似;同理当|Η[w]|<|Η[v]|×ε2时,δ(v,w)<ε。 因此当 |Η[v]|<|Η[w]|×ε2或|Η[w]|<|Η[v]|×ε2时,顶点v和w不相似。 □ 利用上面的削减规则,得到下面判断两个顶点不相似的算法。 算法2disSimWithPrune算法 输入:顶点v和w的结构化邻居Η[v]和Η[w],一个相似性阈值ε(0<ε≤1)。 输出:如果不相似输出true,否则输出false。 1.if(|Η[v]|<|Η[w]|×ε2or|Η[w]|<|Η[v]|×ε2) 2.returntrue 3.else 4.returnfalse 该算法使用引理1来判断两个顶点不相似,如果两个顶点v和w满足引理1中的条件,则顶点v和w一定不相似,输出true,否则不能确定这两个顶点是否相似输出false。 计算图中顶点之间相似性的目的是判断这两个顶点是否相似,根据定义需要计算这两个顶点公共邻居的个数,在给定相似性阈值ε(0<ε≤1)时,如果能够找到使得这两个顶点相似的最小公共邻居的数目,这样在求公共邻居数目时,一旦公共邻居的个数大于使得顶点之间相似的最小公共邻居的数目,就不需要再往下计算其他的公共邻居。为了实现上述思想,本文给出下面的引理。 引理2对于一个给定的相似性阈值ε(0<ε≤1)和顶点v和w的结构化邻居Η[v]和Η[w],设mincount(v,w)为大于等于的最小整数,即那么顶点v和w相似的充要条件是|Η[v]∩Η[w]|≥(v,w)。 利用引理2,算法3给出在不精确计算两个顶点相似性的情况下,确定两个顶点是否相似的算法。 算法3isSim算法 输入:顶点v和w的邻居Nv和Nw,用Nv[i]表示顶点v的第i+1个邻居(其中Nv和Nw中的顶点按照顶点标号的升序排列),一个相似性阈值ε(0<ε≤1)。 输出:如果顶点v和w相似,输出true,否则输出false。 3.counter=2;/*记录已求公共邻居的个数*/ 4.i=0;j=0;/*指示数组下标*/ 5.dv=Nv.length;dw=Nw.length; 6.whilecounter 7.if(Nv[i] 8.dv=dv-1;i=i+1; 9.else if(Nv[i]>Nw[j])then 10.dw=dw-1; 11.j=j+1; 12.else 13.counter=counter+1; 14.i=i+1; 15.j=j+1; 16.end if 17.end while 18.if(counter 19.returnfalse; 20.else 21.returntrue; 22.end if; 算法3中,首先求出使得顶点v和w相似的最小结构化公共邻居的个数(行1~2);然后定义记录已求结构化公共邻居个数的变量counter,因为算法传入的是顶点v和w的邻居顶点,算法后面只是求顶点间公共邻居的个数,并没包含顶点v和w本身,而算法是求结构化邻居的公共顶点个数,因此初始化为2(行3);接着初始化指示数组的下标i=0,j=0(行4);定义两个邻接列表中除已比较的不相等的邻接顶点后剩余的顶点的个数,初始化为对应两个邻接列表中元素的个数(行5);在while循环中求结构化公共邻居的个数(行6~17),当求得的结构化公共邻居的个数大于等于mincount或者除已比较的不相等的邻接顶点后剩余的顶点的个数du,dv的最小值小于使得两个顶点结构化相似的最小结构化公共邻居的最小个数时,没有必要再求后面的公共邻居,直接跳出while循环;最后,判断已求的结构化公共邻居数counter是否小于mincount,如果小于说明两个顶点不相似,返回false,否则两个顶点相似,返回true(行19~22)。 在计算图中的每个连通分量时,本文使用Pregel框架[17]来分布式计算图中所有的连通分量。Pregel将计算过程分为一个个超步,计算开始时标记所有顶点为活动状态。在每个超步中,每个顶点接受上一个超步发送给它的消息后进行处理并更新当前顶点的状态,更新后当前顶点仍为活动状态则将处理后的结果发送给下一个超步,否则该顶点什么也不做,当前超步中每个顶点都处理完成后进入下一个超步,当所有顶点都处于非活动状态时算法结束。下面通过一个简单的例子来介绍使用Pregel计算连通分量的过程。 如图3所示,例如,要求值为1、2、3、4的4个顶点组成的连通分量,白色顶点表示该顶点处于活动状态,灰色顶点表示该顶点处于非活动状态,实线表示顶点之间的边,虚线表示向下一个超步中的顶点发送的消息。初始时4个顶点都处于活跃状态,因此在超步0中,每个顶点都向它的邻居发送自己的当前值,在超步1中,每个顶点接受超步0发送过来的值,如果接收到的值的最大值比当前顶点值大,则更新当前值为接收的最大值,然后将该顶点标记为活跃状态并向邻居顶点发送更新后的值,如果接收到的最大值比当前顶点值小,则将该顶点标记为非活跃状态。例如,第一顶点收到的值为{2,3},其中收到的最大值3大于当前顶点,因此更新当前顶点值为3,将该顶点标记为活动状态并向下一个超步发送该顶点的当前值,第4个顶点收到的值为3,小于当前顶点的值4,标记该顶点为非活动状态,超步2和超步1处理类似,最后在超步3中,由于所有顶点都成为非活动状态,因此算法结束,值相等的顶点在同一个连通分量中。 Fig.3 Computing connected component图3 计算连通分量 基于算法2、算法3、连通分量算法,下面给出基于GraphX的分布式结构化图聚类算法(GXDSGC)。 算法4GXDSGC算法 输入:一个无向无权重图G(V,E),一个相似性阈值ε(0<ε≤1),聚类中顶点的最小个数minNum。 输出:图G中所有的聚类的集合。 1.求出每个顶点的邻居顶点; 2.将每个顶点的邻居顶点作为该顶点的属性值; 3.for在图中的每个邻接顶点对v,wdo 4.if(disSimWithPrune(Nv,Nw))then 5. (v,w).isSim=false; 6.else 7. (v,w).isSim=isSim(Nv,Nw); 8. end if; 9.end for; 10.for(v,w)∈Edo 11.if((v,w).isSim=false)do 12.移除边(v,w); 13.end if; 14.end for; 15.计算图G的连通分量; 16.for每个连通分量CCdo 17.ifCC.num 18. 移除CC; 19.end if; 20.end for; 基于GraphX的分布式结构化图聚类算法(GXDSGC)如算法4所示,算法首先使用GraphX中的两个函数aggregateMessages和outerJoinVertices求出图中每个顶点的邻居顶点并将邻居顶点作为该顶点的属性值(行1~2);然后对图中的每个邻接顶点对v,w求相似性(行3~9),在求相似性时,首先使用削减规则(算法2)判断当前顶点v,w是否不相似,如果不相似设置这两个顶点间的相似性为false(行4~5),否则使用算法3来求这两个顶点之间的相似性(行7);接着移除图中所有不相似的邻接顶点对之间的边,使用4.3节“连通分量算法”求得图中所有的连通分量(行15);然后删除顶点个数小于指定阈值minNum的连通分量;最后求得的连通分量就是所要求的聚类。 本实验所用的软硬件环境如下:集群由5台服务器组成,每台服务器的配置为:Red Hat 64位操作系统,16核CPU,主频1.9 GHz,16 GB内存,2 TB硬盘;Hadoop版本为2.6.0,Spark版本为1.6.0,Java版本为1.8.0,Scala版本为2.10.4。 开发环境配置:操作系统为Windows 732位旗舰版,主频3.10 GHz,4 GB内存,500 GB硬盘;开发工具IntelliJ IDEA Community Edition 15.0.2,Java版本为1.8.0,Scala版本为2.10.4。 实验数据集:本文使用DBLP、Youtube、LiveJournal 3个真实数据集和人工数据集进行实验。其中,DBLP是一个作者协作网络;Youtube是一个用户到用户链接网络;LiveJournal是一个在线社交网络。人工数据集使用文献[18]中的算法生成。数据集统计信息如表1、表2所示。 Table 1 Real datasets表1 真实数据集 Table 2 Synthetic datasets表2 合成数据集 下面将本文中提出的GXDSGC算法和Zhao等人提出的PSCAN算法[13]进行对比实验。实验从运行时间、削减策略和可扩展性三方面来进行比较。PSCAN算法和GXDSGC算法在相同配置的集群上运行,因为PSCAN算法并没有指定聚类的最小尺寸,所以在实验中将GXDSGC算法的最小聚类尺寸设置为2,使得两种算法的结果相同。下面分别从这三方面对GXDSGC算法进行分析。 (1)运行时间 在该实验中,对于不同数据集,在相似性阈值分别取0.6、0.7、0.8、0.9的情况下,分别运行GXDSGC算法和PSCAN算法。算法在表1中数据集上的运行时间如图4所示。 从图4中实验结果可以看出,在相似性阈值不断增大情况下,两个算法的运行时间都逐渐减小,并且GXDSGC算法在4个数据集上的运行时间比PSCAN算法快30多倍,说明该算法和PSCAN算法相比是非常有效的。 GXDSGC算法速度比较快的原因主要有两个:第一个是GXDSGC算法是基于GraphX的算法,当集群的内存足够大时,数据在处理过程中整个数据都在内存当中,中间结果也是存储在内存的,避免了大量的磁盘I/O,节省了大量时间,而PSCAN在Hadoop集群中运行时需要经历多个Mapper和Reducer阶段,即使集群的内存有足够的空间,在每个阶段都需要将中间结果存储在磁盘中,在下一个阶段从磁盘读取中间结果,极大增加了磁盘I/O开销,进而增加了程序的运行时间。第二个原因是GXDSGC算法在计算邻接顶点之间相似性时,通过两种削减策略来计算顶点之间的相似性,在不精确计算顶点间相似性的情况下,判断出两个顶点是否相似,进一步减少了程序的运行时间。 (2)削减策略 为了比较算法中两个削减规则的有效性,在实验时,只记录图中顶点间相似性计算消耗的时间,对于每个数据集运行5次算法,然后对消耗的时间求平均值,得到结果如图5所示。 Fig.4 Running time图4 运行时间 从图5中可以看出,对于每个数据集,使用削减规则和不使用削减规则相比,使用削减规则计算相似性所花费时间明显减少,说明算法中削减规则确实减少了相似性计算消耗的时间。从图5中还可以看出,对于每个数据集,随着相似性阈值不断增大,使用削减的算法运行时间不断减少,这是因为随着相似性阈值不断增大,更多的相似性计算通过削减规则计算出来,说明相似阈值越大,削减规则越有效。 为了进一步比较算法中削减规则的有效性,下面实验使用表2中的合成数据集进行实验。实验结果如图6所示。 Fig.5 Pruning strategy图5 削减策略 Fig.6 Pruning strategy on synthetic datasets图6 合成数据集上的削减策略 首先,保持图中边条数不变,改变顶点个数,使用削减和不使用削减消耗时间如图6(a)所示。然后,保持图中顶点个数不变,改变边的条数,使用削减和不使用削减消耗时间如图6(b)所示。从图6可以看出,无论是改变顶点个数还是改变边条数,使用削减策略能够明显减少相似性计算所消耗的时间。从图6(a)可以看出,随着顶点个数增加,两种算法消耗时间都不断增大,但使用削减算法增幅较小,因为使用削减策略的算法能够通过削减策略减少计算时间。从图6(b)可以看出,在图中顶点个数不变的情况下,随着边条数的增加,没有使用削减策略计算相似性所消耗时间增加,而使用削减策略算法所消耗时间也增加但增幅较小,因为在顶点个数不变的情况下,随着边数的增加,有更多相似性需要计算,所以增加了整个相似性计算时间;对于使用削减的算法,虽然有更多相似性需要计算,但是随着边数的增加,顶点邻居个数会变大,就会有更多之前不能使用削减规则计算相似性的邻接顶点能够通过削减策略判断其相似性,所以随着边条数的增加,计算相似性的时间虽然增加但增幅较小。从图6还可以发现,一个图越稠密,将会有更多的邻接顶点能够通过削减策略判断其相似性,这样削减策略就越有效,就能够明显减少算法在计算相似性时所消耗的时间,加快计算速度。 (3)可扩展性 在该实验中,为了比较GXDSGC算法的可扩展性,对于3个真实数据集,GXDSGC算法的相似性阈值设置为0.6,最小聚类尺寸设置为2,实验结果如图7所示。图7(a)表示在改变集群中机器数的情况下GXDSGC算法在各个数据集上的加速比。图7(b)表示在改变集群中机器数的情况下GXDSGC算法在各个数据集上运行时间的相对加速比。在该实验中,相对加速比的计算公式为: 从图7中可以看出,GXDSGC算法具有良好的可扩展性,且随着数据集规模的增加,算法的加速性能更好,因为随着图尺寸的增加,减少集群中机器间的通信开销在整个运行时间中所占的百分比。从图7(b)中可以看出,算法并没有达到理想的相对加速比,因为集群中机器之间需要进行通信和数据交换,增加了运行时间,使得相对加速比比理想加速比要小。 Fig.7 GXDSGC speedup图7 GXDSGC加速比 SCAN算法利用顶点之间的结构信息不仅能够对图进行聚类,还能识别出图中顶点的不同角色,为用户提供丰富的信息;而PSCAN算法是SCAN算法在分布式集群上的扩展。本文提出的GXDSGC算法是对PSCAN算法的进一步优化,GXDSGC算法在执行过程中能够极大减少I/O开销,并能够通过使用两个削减策略减少相似性计算时间,通过实验表明GXDSGC算法处理数据更加高效,但GXDSGC算法在求连通分量时需要多次迭代,花费大量时间且通信开销也比较大,如何进一步优化算法,降低求连通分量的时间和通信开销仍需进一步研究。4GXDSGC算法
4.1 削减规则1
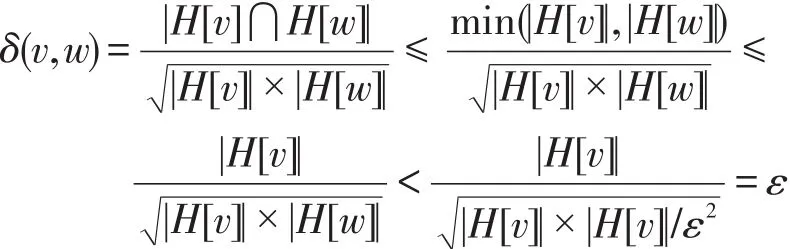
4.2 削减规则2
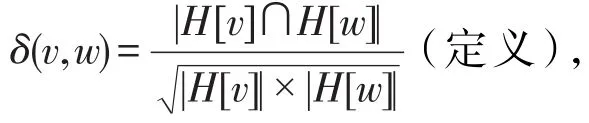
4.3 连通分量计算
4.4 完整算法描述
5 实验与分析
5.1 实验环境配置
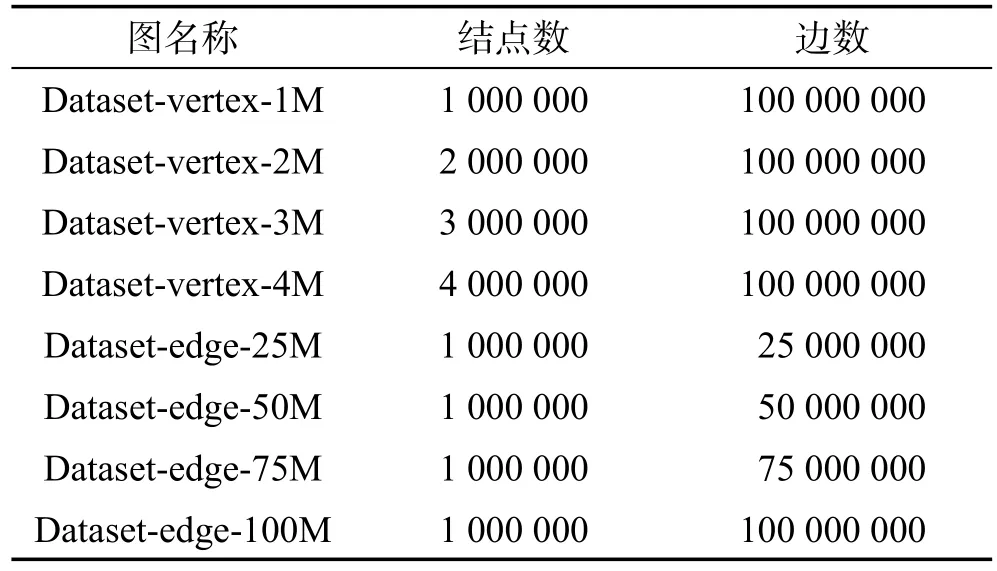
5.2 实验所用数据集
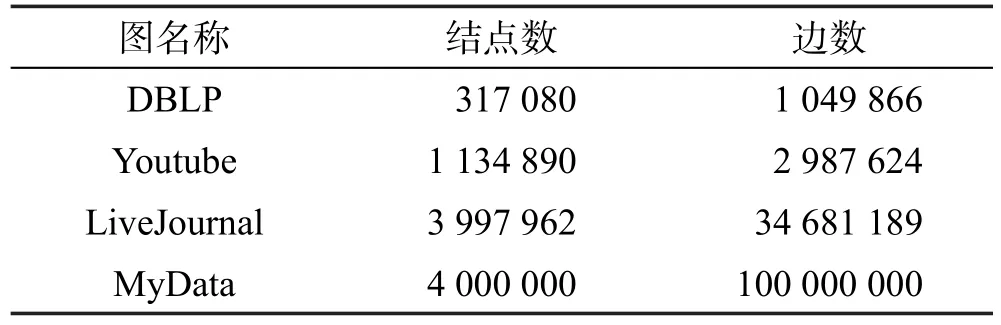
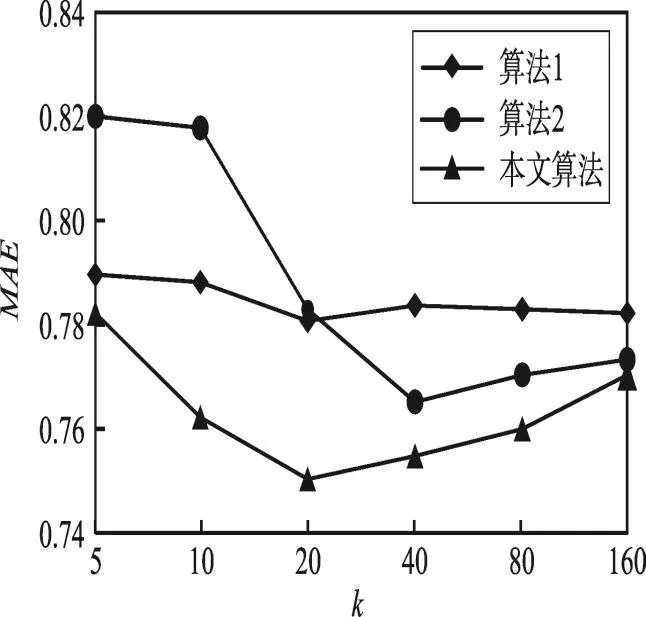
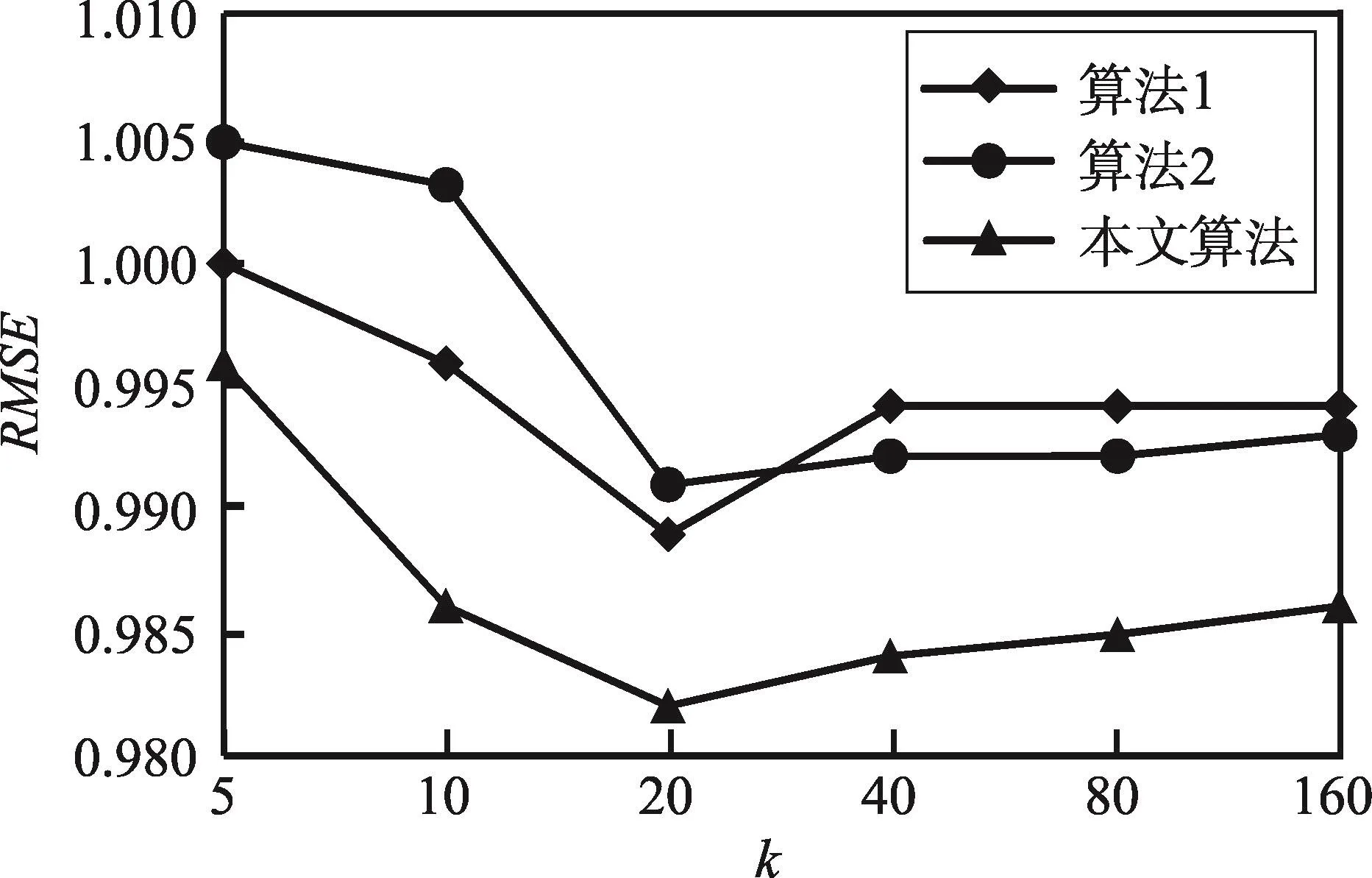
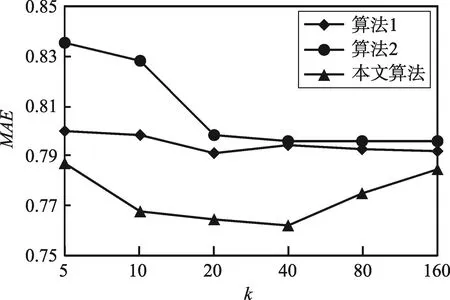
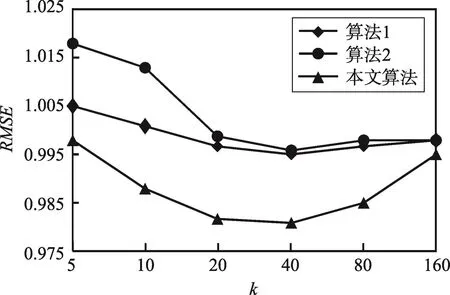
5.3 实验结果及分析

6 结束语
