基于统计能量分析的热效应对高频声振响应影响研究

王用岩，金伟，付焕兵，黄虎

（中国航空工业集团公司 成都飞机设计研究所，成都 610091）

随机激励下结构声振响应问题是工程中的常见问题，如高速飞行器在飞行过程中会面临复杂的振动、噪声和热环境[1-3]，此时热效应对声振响应的影响不可忽略。针对此问题，相关学者开展了一系列涉及热效应的声振响应分析研究。Avsec等[4]进行了简支梁和固支梁在热环境下声振响应分析，Jeyaraj等[5]，Liu和 Li[6]，Kumar等[7]分别研究了热效应对各向同性板、复合材料板和功能梯度材料板声振响应的影响。这些研究主要集中在中低频段，在高频段热效应对声振响应影响的研究鲜有报道。

高频声振响应问题的求解方法有统计能量分析（Statistical Energy Analysis, SEA）、能量有限元等。Zhang等[8]和 Wang等[9]利用能量有限元法分别研究了热效应对高频激励下梁和板声振响应的影响。统计能量分析是现阶段高频声振响应问题最常用的求解方法，针对此方法已经有比较多的研究[10-11]，但是目前鲜见专门针对SEA的热效应影响研究。

板壳结构是统计能量分析中最常用的子系统，文中以L型耦合板为例，研究热效应对统计能量分析中重要参数的影响。分别利用波法和有限元法（Finite element method, FEM）分析了不同温度下材料参数和热应力对耦合损耗因子的影响，以此来得到热效应对高频声振响应的影响规律。

1 统计能量分析

统计能量分析是求解高频声振响应问题的有效方法，现在已经广泛应用到航空航天等各领域。在统计能量分析中，能量是主要控制变量，其他变量如位移、应力等，均由能量计算而来。能量平衡方程为[10]：

式中：L是由耦合损耗因子和内损耗因子组成的矩阵；E是各子系统能量；Pin是输入功率，f是分析频带的中心频率。由式（1）可知，要求得各子系统的能量分布，需要确定三个重要参数：输入功率、内损耗因子和耦合损耗因子。

对于单点激励，板的输入功率为：

式中：｜F｜为激励力的幅值；Zm为激励点的阻抗，当分析频率较高时，与无限大结构的阻抗 Z∞相近。无限大板的阻抗为：

式中：Y、ρ和 μ分别为材料的弹性模量、密度和泊松比；h为板的厚度。热效应对输入功率的影响主要体现在材料参数的变化上，主要是弹性模量的变化。

内损耗因子大小为子系统阻尼比的2倍，通常由试验测得。热效应对它的影响同样体现在材料参数的变化上。热效应对输入功率和内损耗因子的影响较为单一，文中不再作具体分析。相对而言，热效应对耦合损耗因子的影响较为复杂，一方面是温度变化引起材料参数的变化，主要是指材料弹性模量发生变化，另一方面是热应力的影响，使得结构刚度发生变化。耦合损耗因子最常用的计算方法是波法[12-13]，但是此方法仅能考虑材料参数变化造成的影响，而不能考虑热应力的影响。有限元法能够有效解决中低频声振响应问题，求得结构的耦合损耗因子[14-15]。在某些情况下，如结构简单、网格划分密集时，可进行拓展从而解决中高频问题[16]。文献[14-16]的计算结果表明，虽然有限元法计算出耦合损耗因子与波法结果不完全一致，但是也有一定的参照意义。文中在这些工作的基础上，结合有限元法在处理热问题和预应力问题时的优势，利用有限元法分析热效应对耦合损耗因子的影响，进而得到热效应对高频声振响应问题的影响，具有一定的工程参考意义。

2 耦合损耗因子计算

文中在计算耦合损耗因子时主要利用的是有限元法，波法计算出的结果作为参照对比。SEA中最常用的子系统为梁和板结构，文中选取典型的L型耦合板为研究对象，梁的计算结果与此类似。

2.1 波法计算

L型耦合板如图 1所示，利用波法[14-15]对两板间的耦合损耗因子进行计算。如图1所示，两板在相应坐标系下的三个位移分量分别为un、vn、wn（n=1,2，为所在板的编号）。入射角为 θ的弯曲波入射时，将在两板上产生反射行波、透射行波以及反射近场波、透射近场波，弯曲、拉伸和剪切波与x轴的夹角分别为 αn、βn、γn，则 α1=θ。

由Snell定律得，一列行波在边界发生反射或透射时，其反射波或透射波在平行于边界面的方向波数必须相等，即有：

式中：kBn、kLn、kTn分别为板n的弯曲波数、拉伸波数、剪切波数，可由式（3）求得：

式中：f为分析频率；cBn、cLn和cTn分别为三种波的相速度。

各种波的具体形式表示如下：

反射和透射近场波

投射和反射拉伸、剪切波与式（7）类似。根据边界处的位移连续条件，转角连续条件，弯曲平衡条件和力平衡边界条件，可将波的能量求出。

对混响声场，板1弯曲入射波对板2弯曲波的耦合损耗因子为：

式中：l12为两板交线长度；A1为板 1面积；cg1为波群速度。其他各种波形对应的耦合损耗因子可用类似方法求出。

2.2 有限元法计算

结构振动方程的有限元形式为[17]：

式中：Ks、Cs、Ms分别为结构的刚度、阻尼和质量矩阵；dj为节点位移；Fs为激励力；ω为圆频率。

利用有限元法可求得节点位移，进一步可求出结构的振动能量为：

式中：EKE和EPE分别为振动的动能和势能最大值。

当温度变化不大时，材料的密度通常变化不大，故 Ms保持不变；材料阻尼(内损耗因子)随温度的变化这里也不再考虑，故 Cs保持不变。热效应对刚度矩阵的影响分为两方面：一是材料参数随温度变化，引起弹性模量发生变化；二是热应力引起刚度矩阵发生变化。

当温度发生变化时，式（11）修正为：

式中：KT是材料参数变化引起的刚度矩阵变化量；Kσ是热应力引起的附加刚度矩阵。求解式（12）后，再利用式（11）可求得考虑热效应后结构的振动能量。

当只有两个子系统时，SEA的控制方程为：

式中：ηn、En、Pn分别为板n的内损耗因子、振动能量和输入功率；η12和η21为两子系统间耦合损耗因子。

当两个子系统相同时，η12=η21；如果只在子系统1上施加激励，则P2=0，由式（14）得：

板的振动可分为三种形式，即弯曲、拉伸和剪切振动。在SEA中，这三种振动被区分为三类子系统。在FEM中，这三种变形耦合到一起难以区分。在薄板假设条件下，结构在受到垂直于板面方向的激励时主要为弯曲振动，此时可近似地把板的振动能量等效为弯曲波的能量。在式（15）中，内损耗因子是已知的，子系统的能量通过计算得到，然后可求出结构间弯曲-弯曲的耦合损耗因子，这也是SEA中最常用的耦合损耗因子。

3 算例研究

3.1 分析模型

文中采用典型的L型耦合板为研究对象，如图2所示。激励位置为板1中心处，激励力为幅值为1 N的简谐力，除耦合边外其他边均固支。

板的材料为铝合金，边长为0.4 m，厚度为6 mm，材料参数见表1。弹性模量随温度变化而变化，随温度变化的材料参数H可表示为[18]：

式中：H0、H-1、H1、H2和H3为温度T的系数，见表2。计算可得，材料弹性模量在20 ℃ （293 K）时为 71.1 GPa，60 ℃时为 66.5 GPa，320 ℃时为47.7 GPa。

表1 板材料参数

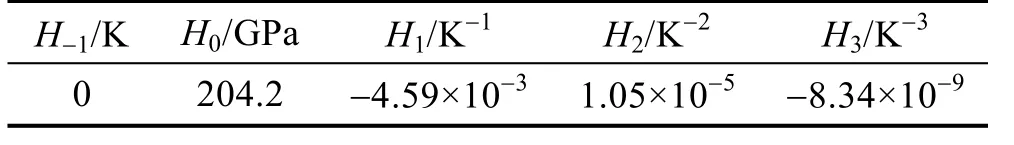
表2 铝合金弹性模量的热相关参数

SEA主要用于处理高频问题，耦合损耗因子在高频段才具有意义。同时，由于FEM在处理高频问题时具有限制，计算频率不能过高，因此文中设置的分析频带为400～5000 Hz，计算的频率间隔为20 Hz。

3.2 FEM计算结果验证

有限元分析使用软件ANSYS完成，板结构采用Shell181单元进行计算。因分析频率较高，故网格需划分十分密集，为了兼顾计算效率和计算精度，需对网格收敛性进行考查。经过验证，0.002 m的网格可以满足计算精度要求。

利用波法和有限元法计算出板的耦合损耗因子如图3所示，FEM 计算结果在频域上存在一个比较大的波动。为了便于与波法结果作比较，需将 FEM计算结果拟合为一条光滑的曲线。直接将FEM曲线进行拟合结果并不理想，由于波法计算出的耦合损耗因子在双对数坐标下为一条直线，因此在双对数坐标系下将FEM计算出的耦合损耗因子进行拟合。FEM曲线上的数据点(xi, yi)，转化到对数坐标下变为(lg(xi),lg(yi))，利用最小二乘法拟合为直线 y=kx+b, 则转化到线性坐标下的曲线方程为lg(y)=klg(x)+b，在图中记为”Fitted FEM”。

由图3可知，波法和拟合前的FEM计算结果在高频段比较接近，在低频段差距较大。造成这一差距的原因是多方面的：第一，两种方法在输入功率计算和边界条件处理等方面有所不同，尤其在低频段，边界条件造成影响较大；第二，波法主要用于求解频率较高时的耦合损耗因子，而FEM则主要用来解决低频问题，这两种方法在求解时存在自身的局限性；第三，FEM计算时将所有的能量等效为弯曲振动能量，而波法同时考虑了弯曲、拉伸、剪切三种波形，这也会造成一定误差。拟合后的FEM与波法计算出的耦合损耗因子相比，整体趋势上一致，具体数值上有一定差距，但是差距有限。

总的来说，利用FEM和波法计算出的耦合损耗因子，虽然存在一些差距，但是从整体上看，两种方法的计算结果仍然是相近的，其他文献[10,15]的一些计算结果也在某种程度上说明了这一点。在 SEA中，波法是最常用的耦合损耗因子计算方法，其计算结果已经得到认可，通过FEM和波法的计算结果对比，说明对于文中所研究的 L 型耦合板结构，在关注的频带（400～5000 Hz）范围内，利用FEM计算出的耦合损耗因子是可信的。

3.3 不同温度下材料参数对耦合损耗因子的影响

在不同温度下，结构材料参数有所不同，主要是弹性模量发生变化。20 ℃和 60 ℃时计算出的板耦合损耗因子如图4所示。从图4可知，波法计算出的不同温度下耦合损耗因子几乎完全一致，FEM 计算出的结果在横坐标上有一个比较小的偏移量，对结果影响不大。

20 ℃和 60 ℃时板的固有频率见表 3，可以看出，60 ℃时板的各阶固有频率相对于 20 ℃时变化很小，减小约为3.23%。不论低阶还是高阶固有频率，其减小幅度是一致的。可以用四边简支矩形薄板的固有频率计算公式对此现象进行说明。

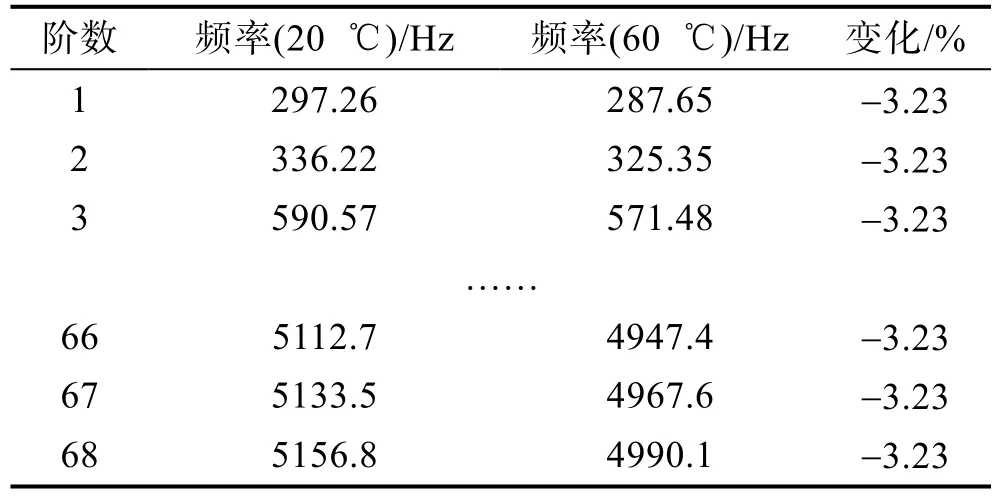
表3 不同材料参数下板的固有频率

长和宽分别为a和b的矩形薄板，第(i, j)阶的弯曲固有频率ωi,j为：

则板的各阶固有频率变化率为：

将温度变化的幅度增大，在 320 ℃时材料的弹性模量为 47.7 GPa，结构的模态特性也会有显著变化。由式（18）可知，320 ℃时板的各阶固有频率相对于20 ℃时大约减小18%。此时，板的耦合损耗因子如图5所示，与固有频率的变化规律相同，当温度升高后，耦合损耗因子在整体上有所减小。利用波法计算出的耦合损耗因子，320 ℃的值小于20 ℃时的值 10%左右，FEM 的计算结果虽然与波法有一定差距，但是在温度改变时曲线变化规律与波法一致，这从某种程度上也证明了FEM计算耦合损耗因子方法的可靠性。

总的来说，温度变化时材料参数的改变会使结构间耦合损耗因子整体上发生变化，当温度升高时材料弹性模量减小，对应的耦合损耗因子有所减小，温度降低时结果相反。耦合损耗因子变化的幅度由温度改变的大小控制，当温度变化较小时（40 ℃），材料参数变化对耦合损耗因子的影响可以忽略不计；当温度变化较大时（300 ℃），耦合损耗因子受一定影响，但变化幅度并不是特别大。

3.4 热应力对耦合损耗因子的影响

如图 2所示的四边固支板，温度由 20 ℃变为60 ℃时，固支板受到压应力作用，其应力分布如图6所示。除个别应力集中位置处，板的绝大部分位置应力为100 MPa左右，这已经可以表征出比较恶劣的温度变化环境。

零应力（Standard）和压应力（Δt=40 ℃）作用下板的固有频率见表4。从表4中可以看出，压应力作用后板的固有频率有所减小，尤其是前几阶固有频率减小的幅度很大，当阶次升高后，两种状态板的固有频率变得比较接近。第66到68阶固有频率，两者的差距不超过 4%。两种状态下计算出的耦合损耗因子如图7所示，其分布规律与固有频率一致，均是在频率较低处有一定差距（拟合曲线“中和”了原曲线的一些细节，因而比较接近），在频率较高时压应力的作用对板的耦合损耗因子几乎无影响。

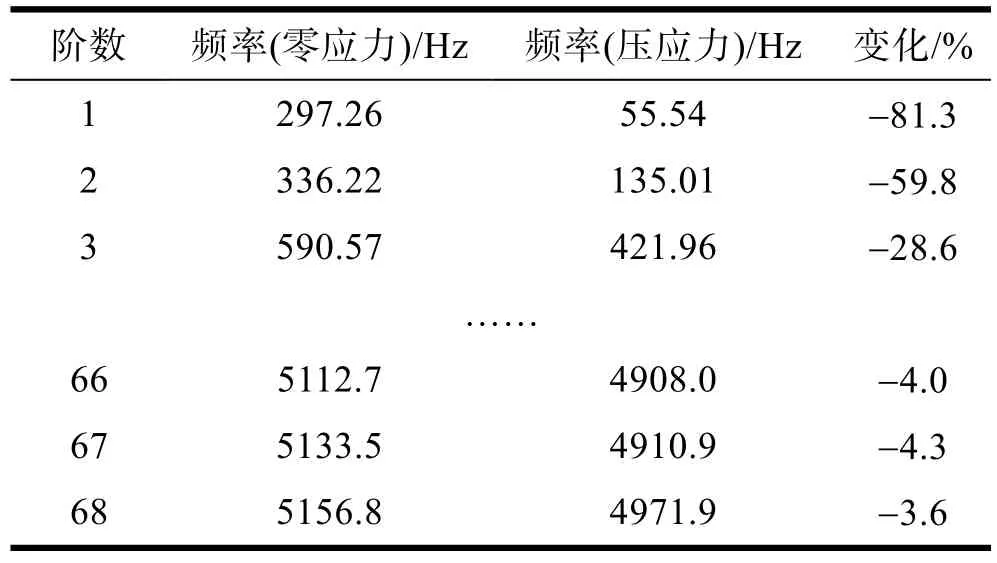
表4 压应力(20～ 60 ℃)作用下板的固有频率

零应力和拉应力作用下板的耦合损耗因子如图8所示，曲线分布规律与如图7一致，拉应力作用使得频率较低处板的耦合损耗因子产生了一定变化，而对频率较高处计算出的耦合损耗因子影响很小。热应力的施加会使结构的固有频率产生一定变化，其中，拉应力会使结构固有频率增大，压应力会使结构固有频率减小。预应力会使结构前几阶固有频率产生比较大的变化，而对高阶固有频率的影响有限。与之相对应，预应力的施加会使低频段结构的耦合损耗因子产生比较大的变化，而对高频段的耦合损耗因子影响较小

3.5 热应力对耦合损耗因子的影响

将材料参数变化和热应力的影响叠加，综合考虑热效应对耦合损耗因子的影响。当温度由20 ℃变为60 ℃时，热效应对 L型板固有频率的影响见表 5。该表可以看作是表3和表4的叠加。热效应使低阶固有频率变化较大，这主要是热应力作用的影响。此时，材料参数变化和热应力对结构的高阶固有频率影响不大，故此时热效应的影响也有限。

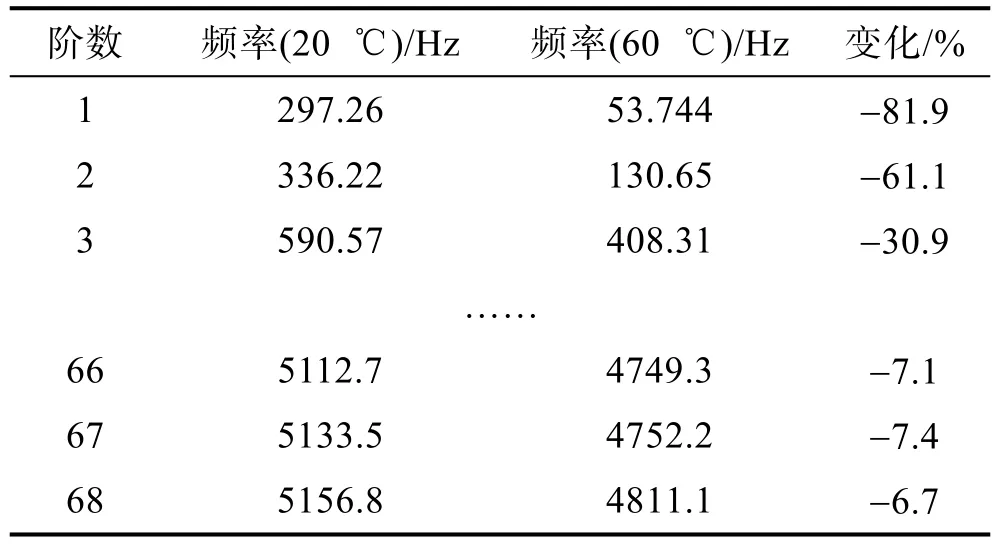
表5 热效应对板固有频率影响

当温度由 20 ℃变为 60 ℃时，热效应对 L 型板耦合损耗因子的影响如图9所示。由于温度变化幅度比较小，材料参数变化有限，所以热效应的影响主要体现在热应力作用上。因此，图9中曲线与图7类似，在低频段热效应的影响较明显，在高频段热效应的影响有限。

5 结论

有限元法在工程中常用于解决低频问题，但是在结构简单、网格划分足够密集时可作适当拓展用于解决中高频问题。在400～5000 Hz频带范围内，文中利用FEM 计算了L型板线连接的耦合损耗因子，其计算结果与波法计算结果基本一致，证明了FEM计算耦合损耗因子的有效性。

热效应对耦合损耗因子影响可分为两方面：一方面是温度变化引起材料参数变化；另一方面是温度变化会使结构受到热应力作用。以固支板为研究对象，利用波法和 FEM，研究了温度变化时材料参数变化对耦合损耗因子的影响：在温度升高时，材料弹性模量降低，会使结构的各阶固有频率有所降低，耦合损耗因子在整体上会有所减小；温度降低时结果相反。利用 FEM研究了热应力对耦合损耗因子的影响：热应力对模态的影响主要体现在低频段，对高频段的影响有限；与之相对应，热应力对低频段（此低频段指的是在400～5000 Hz中频率相对较低的频段，实际上也属于高频范畴）耦合损耗因子的影响较大，对高频段耦合损耗因子的影响较小。

分析计算表明，在通常情况下，热效应对耦合损耗因子的影响，低频段需要考虑材料参数变化和热应力共同作用，而在高频段主要考虑材料参数变化即可。热效应对耦合损耗因子的影响，实际上体现的是热效应对声振耦合问题响应的影响。当温度变化较大时，热应力较大，此时热效应对 SEA 的影响不可忽略，尤其是在低频段，热效应的影响更为明显。