全复合材料翼面振动主动控制技术研究

2018-10-12雷鸣李阳寇宝智

装备环境工程 2018年9期

雷鸣，李阳，寇宝智

（中国飞行试验研究院飞机所，西安 710089）

相较于传统的金属材料，复合材料具有比强度、比刚度高、耐腐蚀、可设计性等诸多优点，在飞机结构设计中得到了广泛的应用。机翼作为飞机提供升力的重要部件，也越来越多地应用到了复合材料上，飞机的平尾和垂尾也大量应用了复合材料。另一方面随着飞机性能的不断提高，飞机的振动问题越来越突出。在某些高性能双垂尾战斗机上，如美国的F-14、F-15、F-16、F-18和F-22等[1-4]，常常发生一些典型的振动问题。国内型号试飞过程，多次出现严重的飞机振动问题。

为了解决复合材料翼面结构可能出现的振动问题，文中进行了全复合材料翼面振动主动控制技术研究。振动主动控制是根据传感器检测到的结构振动，应用一定的控制策略，经过实时计算，驱动作动器对结构或系统施加一定的力或力矩，以控制结构或系统的振动。美国已经将振动主动控制技术应用在了一些柔性空间结构和直升机机身上，B-1B、F-15、F-16和F-18飞机上已经使用了振动主动控制技术[5-6]。

为了应对飞机复合材料结构出现的某些振动问题，文中将使用 MFC（Macro Fiber Composites，MFC）压电作动器作为控制作动器，针对全复合材料翼面结构展开结构振动主动控制技术研究。通过结构建模、控制律设计、仿真实验以及地面试验，为解决飞机的振动控制问题寻找高效的办法。

1 全复合材料翼面仿真建模

被控对象为带后掠角的全复合材料翼面，1/4弦线的后掠角为45°，翼型选用NACA65004翼型。该翼面采用全复合材料结构设计，即翼梁、翼肋和蒙皮均采用全复合材料制造。翼面模型结构主要包括蒙皮、梁缘条、梁腹板、（泡沫）填充物、配重杆、配重，翼面的主要承力部件为翼梁，翼梁设计为复合材料盒式梁。

选择压电复合材料粗纤维复合材料MFC为控制作动器。压电作动器应布置在相应模态的应变能最大处[1,7-8]。压电作动器安装位置和加速度测量点如图 1所示。

建立压电作动器激励仿真模型。设带有压电作动器的复合材料结构翼面有阻尼振动微分方程为[9]：

式中：m、c、k分别为翼面结构的质量矩阵、阻尼矩阵和刚度矩阵；y代表翼面各自由度的位移；Ritz矩阵 Tr为加入单位电压时压电作动器使得翼面结构产生的变形量。将上述振动方程经过一系列转变得到状态空间方程[10]。

首先利用有限元分析软件计算两组压电作动器分别作用时机翼结构的位移，再将它们组合得到 Tr矩阵。结构试验机翼的振动是小变形线性的，将上述振动方程通过坐标变换转化为模态坐标下的振动方程，引入如下坐标变换公式：

将式（3）表示为：

式中：M、C和K分别为模态坐标下的质量、阻尼和刚度矩阵。

由于 Ritz向量取静变形，导致上述方程为刚性方程，为克服这个问题，再将坐标进行转换。令，式中 W为“质量矩阵”M的右奇异值矩阵，将其带入式（4）可得，并给等式两边同时左乘以“质量矩阵”M的左奇异值矩阵U的转置。

则上述方程可简化为：

2 控制律设计与仿真结果

2.1 理论基础与建模

在连续控制系统中[11]，按偏差的比例（P）、积分（I）和微分（D）进行控制的PID控制器获得了广泛的应用，它具有结构简单、参数易于调整和适应性广等特点，对于那些动态模型不准、参数变化较大的控制对象，采用 PID控制往往能得到满意的控制效果。PID控制是一种线性调节控制，把设定值和实际输出值相减，得到控制偏差经比例、积分和微分运算后通过线性组合构成控制律的输出，即控制量u(t)。PID控制规律为：

PID 控制参数 KP、Ti和 Td相互独立，参数整定比较方便。使用中根据对象特性、负荷情况，合理选择控制规律是至关重要的。确定这些参数可通过理论分析方法，也可以采用实验方法，特别是系统被控对象参数模型不准时，通过实验方法确定控制器参数较为有效。实际中常用的参数确定方法有试凑法、临界比例度法以及多渡过程响应法。由这些方法得到的参数值在使用时不一定是最好的，在投入运行时，可以在这些值附近做一些调整，已达到更好的控制效果。文中对KP、Ti和Td参数的选取采用试凑法，取P=KP，I=KP/Ti，D= KP·Td。

控制律设计实现框图如图2所示。利用MATLAB中的Simulink仿真平台设计PID控制律。PID控制仿真系统图如图3所示。

2.2 变参分析

分析控制律中的三个参数：比例参数P、积分参数 I和微分参数 D对控制效果的影响。随着参数 P的变化，翼梢后缘测点振动幅值变化见表1。

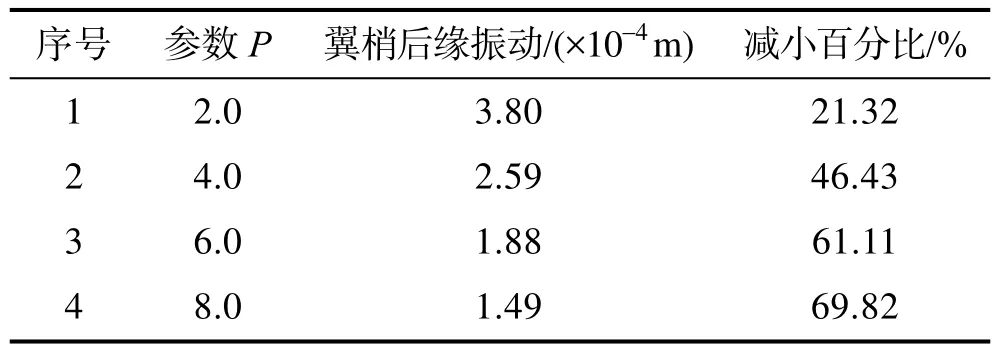
表1 参数P变化对控制效果的影响

不同 P值下翼面梢部后缘测点振动位移时间历程如图4所示。分析仿真结果发现，随着P值的增加振动幅值减小，但不能无限增加P值。一方面，随着P值的增加，控制律输出会越来越大，当达到门限值时，控制效果提高不会很明显；另一方面，P值的增加也意味着控制能量的增加。

随着I值的变化，翼梢后缘测点振动位移响应幅值见表2。不同I值下，翼面梢部后缘测点的振动位移时间历程如图5所示。积分控制是对输出误差进行积分，将得到的信号反馈到输入，是为了消除输出误差的静差。文中直接采用振动响应位移作为反馈信号，没有将该信号与设定值相减，该信号不属于误差信号，不会出现静差。由表2和图5可以看出，随着参数I的增加，振动响应越来越大。

表2 参数I变化对控制效果的影响

随着 D值的变化，翼梢后缘测点振动位移响应幅值见表3。不同D值下翼面梢部后缘振动位移时间历程如图6所示。微分控制器单独作用时，随着参数D的增大，振动控制效果越来越明显，振动幅值越来越小，当 D值增大到一定程度时会导致发散。根据以上对PID参数的分析，发现参数P和参数D的增加都会使振动减小，而参数I的增加使振动增加。

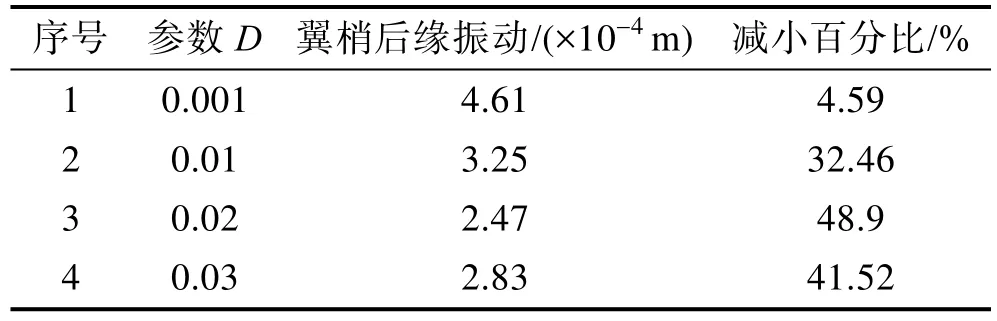
表3 参数D变化对控制效果的影响

使用PID方法进行振动主动控制时，当控制律参数P和D越大，控制律输出越大，振动幅值减小越快，并且稳定值越小。当参数I越大，响应幅值增大，因此最终将I值设为0。控制参数不能无限增大，一方面参数的增大意味着需要的控制能量增大，系统负担增大；另一方面参数设置过大可能导致发散。因此文中通过选取参数P和参数D使控制效果达到最佳。同时设置P参数和D参数时，翼梢后缘的控制效果时间历程如图7所示。

3 振动主动控制地面试验

3.1 地面试验简介

结构振动主动控制地面试验系统基本原理：在不同激励条件下，由试验者通过控制盒设置面板选择控制律方法和激励信号发送至控制计算机，按照控制规律生成相应的控制信号，在有效的安全监控下输入至压电放大器测试端口，放大后的电压送入压电作动器，据此实现对结构的激励，实现复合材料翼面振动主动控制。翼面结构振动主动控制系统工作过程如图11所示。为振动主动控制地面试验如图12所示。在翼尖布置两个振动传感器，一个用于振动主动控制反馈计算，另一个进行响应测量。试验过程中，首先用激励器对翼面翼尖进行激励，之后通过控制盒启动振动主动控制系统，进行控制。

3.2 试验结果

根据仿真试验所设计的 PID控制律参数，开展全复合材料机翼的振动主动控制地面试验。翼梢后缘的控制效果时间历程如图10所示，振动响应减小79.74%。

3.3 问题分析

地面试验与仿真试验不同之处在于地面试验中存在时间延迟，会对结果造成一定的影响。某一组地面试验和仿真试验的激励信号和加速度响应信号如图11所示。

从图11a可以明显看到激励信号在0.35 s前已经加入，而翼梢后缘测点2直到0.35 s以后才有响应，明显可以看出系统中存在时间延迟。而仿真中就不存在这样的情况。从图11b可以明显看出，激励时间和响应时间基本是同一时刻开始变化。不同的延迟时间会对控制造成不同的影响，有可能会使控制效果变差，反而使控制下的振动增加。