一种线性电路状态空间模型的提取方法

丁家峰，梁 健，李新梅，丁一鹏，赵 岩

（中南大学 物理与电子学院，长沙 410012）

0 引言

电路的动态分析是电路分析的重要组成部分，是了解电路系统动态复杂行为的重要手段。对电路进行动态分析，常常使用节点分析法和状态变量法。节点分析法是早期用于处理电路直流分析而建立起来的方法，后来经过发展常被用于电路的动态分析中[1]。使用节点分析法对电路进行动态分析时，一般使用数值积分法将储能元件如电容、电感等效为电流源与电阻的并联或串联，从而在每一个时刻点将电路等效为电阻网络进行求解[2,3]。由于无法得到任意时刻的电路状态，近年来，对节点分析法研究仅限于如何加速求解过程，很少涉及电路理论本身[4]。

状态变量法是分析电路的有力工具，其最早应用于控制系统分析，后来被广泛运用到电路网络的动态分析中。状态变量法对系统进行分析的关键是提取出系统的状态方程。状态方程是用一组状态变量和输入信号共同描述的微分方程组。状态变量一般是系统内部的量，在线性网络中，一般选取电容电压和电感电流作为系统状态变量[5]。使用状态变量法分析电路，相比其他的分析方法，具有如下优点：1）无论是线性电路还是非线性电路，只要找出合适的状态变量，都可以使用状态变量法进行分析[6]；2）只要得到电路在某个时刻t0的一组状态变量，就可根据状态方程得出任一时刻t（t＞t0）的电路状态；3）使用状态变量法对电路进行分析，最终都会得到一组一阶微分方程，其十分便于利用计算机进行求解。因此，状态变量法常常被用于系统的建模和分析中[7]。但是系统状态方程的提取不是一个简单的问题，传统的以电容电压和电感电流作为状态变量的提取方法一般通过复杂的网络分析得到标准形式的状态方程，其过程包含了复杂的网络图论理论[8]。这种方法列写状态方程十分复杂，有时甚至不能得到标准形式的状态方程。为了使用状态变量法分析电路方便研究工作，人们提出了一些非标准形式的状态空间模型[9,10]，最常用的就是基于系统传递函数的状态空间模型。根据系统传递函数提取系统状态方程的问题被称为传递函数的实现问题。如果选取的状态变量不同，根据传递函数可以得到不同的状态方程。每个状态方程被称为传递函数的一个实现，其中能控规范形和能观规范形是最基本的两种实现[11]。这类状态方程与标准的状态方程的不同之处在于其不能保证选取的状态变量为电容电压或者电感电流，甚至有可能是一个不存在物理意义的量。但这类状态方程十分便于对系统进行描述与分析，特别是在控制系统理论中运用十分广泛，一般可以根据这类状态方程去构造真实的物理系统，对其提取方法进行研究是一件十分有意义的事情[12]。要想获得这类状态方程，就必须先得到系统的传递函数。对于简单的电路和系统，其传递函数可以通过计算直接得到，但复杂电路和系统的传递函数较难求取，往往只能通过实验或者拟合的方式得出，这给状态方程的提取带来了困难。

为了解决复杂电路和系统求取传递函数中存在的困难，方便得到传递函数的状态空间实现，本文提出了一种适用于线性电路的状态空间模型提取方法。该方法将电路复频域分析方法和改进节点法相结合，使用符号运算求解出线性系统的传递函数，通过传递函数提取出单输入——单输出系统的能控规范形和能观规范形两种基本实现。

1 线性系统的状态空间描述

单输入——单输出系统的状态空间描述可表示为：

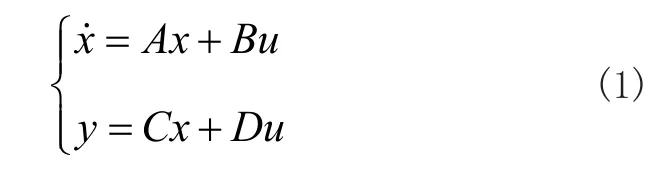
其中，x为状态变量，u为系统输入，y为系统输出，A为系统矩阵，B为输入矩阵，C为输出矩阵，D为耦合矩阵。在传递函数的多种状态空间实现中，能观规范形实现和能控规范形实现为最基本的两种实现方式。

考虑物理可实现的单输入——单输出系统的传递函数：

其中，G(s)为严真情形，d为直接输入分量。根据传递函数，可得出单输入——单输出系统的能控规范形的系数矩阵为：

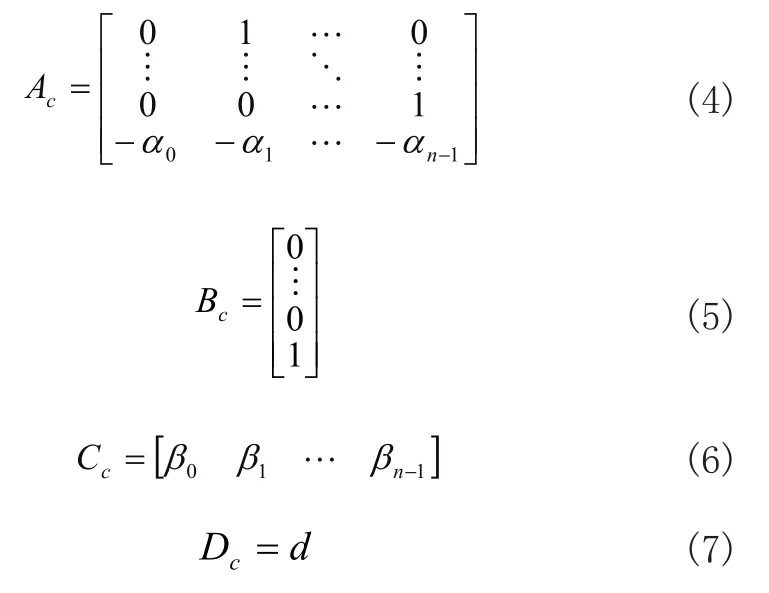
单输入——单输出系统的能观规范形的系数矩阵为：

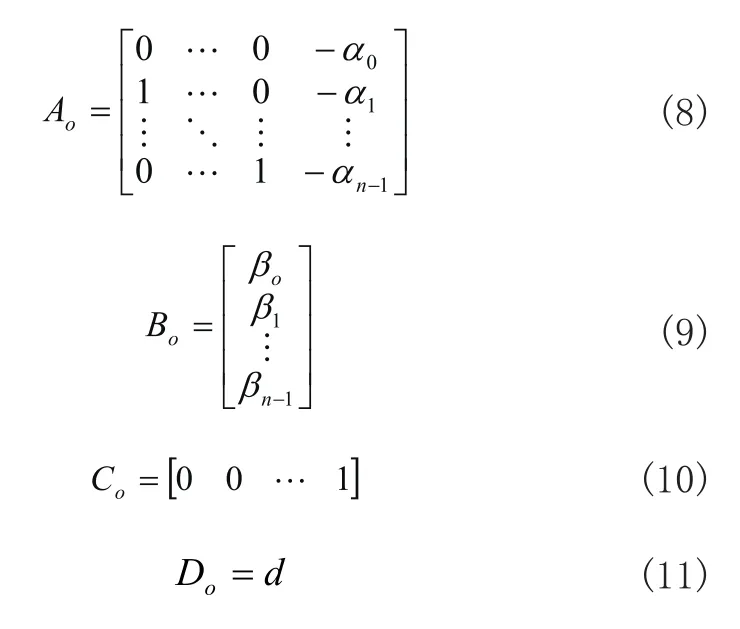
2 算法分析与设计

观察系统规范形实现的系数矩阵可知，如果已取得系统的传递函数，可将传递函数变换出严真情形，提取出分子和分母多项式的系数，根据这些系数便可构成系统规范形实现的系数矩阵。因此，如何提取系统状态方程的问题可以转变为如何求取系统传递函数的问题。根据传递函数，我们用算法实现了单输入——单输出系统的能控规范形实现和能观规范形实现这两种基本状态空间模型的提取，其算法流程图如图1所示。

图1 算法流程图

2.1 基于线性电路复频域方法的电路元件参数分析

在电路分析领域，通常把系统输入称为激励，记作f(t)，把系统输出称为响应，记作y(t)，系统传递函数可以表示为：

其中Y(s)和F(s)分别为零状态下y(t)和f(t)的拉普拉斯变换。根据式(12)可知，要想得出系统的传递函数，必须先求出系统激励和响应的拉普拉斯变换。本文使用线性电路复频域分析的方法求出电路网络激励与响应的拉普拉斯变换。

在线性电路复频域分析中，常常使用元件的S域模型，将时域的电路转换为S域的电路；再根据基尔霍夫定律对S域电路列线性方程组进行求解，便可得到各个电路变量的拉普拉斯变换。由于拉普拉斯变换的线性性质，基尔霍夫定律在S域下的形式和时域下的形式相似，可以简单表示为：对于任一节点，对任一回路，。根据元件的电压与电流的时域关系和拉普拉斯变换的性质，可以得出各个元件的S域电路模型。

对于电阻元件，其电压电流的时域关系为u(t)=Ri(t)，两边取拉普拉斯变换，可得到电阻元件的S域关系形式为U(s)=RI(s)。因此，电阻的S域电路模型如图2所示。

图2 电阻S域电路模型

图3 电感S域电路模型

图4 电容S域电路模型

对于电源元件，S域下的关系式为时域下关系式的拉普拉斯变换。其他的线性元件也可以根据拉普拉斯变换的性质得到S域的电路模型。

由上述可知，在时域中，电感及电容的电压与电流之间的微分关系，在S域中变成了线性关系。因此，时域中的电路微分方程组，在S域中变成线性代数方程组，求解这个方程组，可以得到电路中有关电流和电压的拉普拉斯变换，再根据激励和选取的响应（已求得）的拉普拉斯变换，按式(12)求得响应与激励之间的传递函数。那么，使用怎样的方法在计算机环境下生成S域电路线性代数方程组？本文采用的是改进节点法。

2.2 基于改进节点法的电路网络矩阵生成

改进节点法是常用的建立电路代数方程组的方法，其具有方便、快速等优点。许多仿真软件如Spice使用了改进节点法建立代数方程组。

改进节点法的基本思想是将元件分为了三类。第一类是可用复电导描述的元件，包括电阻、电感和电容，它们的复电导分别为1/R、1/sL和sC；第二类是不能使用复电导描述的元件，主要包括独立电流源和各种受控源；第三类元件为独立电压源。改进节点法根据三类不同元件对生成的代数方程组的贡献，将元件贡献填入代数方程组中，最终生成代数方程组TX=B。在这一过程中，第一类元件应最先被处理，这类元件的贡献是构建出最基本的系数矩阵T，此时解向量X为节点电压。第二类元件和第三类元件的处理顺序可以任意选择，其中独立电流源主要对右端向量B有贡献，各类受控源和独立电压源对系数矩阵T、右端向量B以及解向量X皆有贡献[13]。

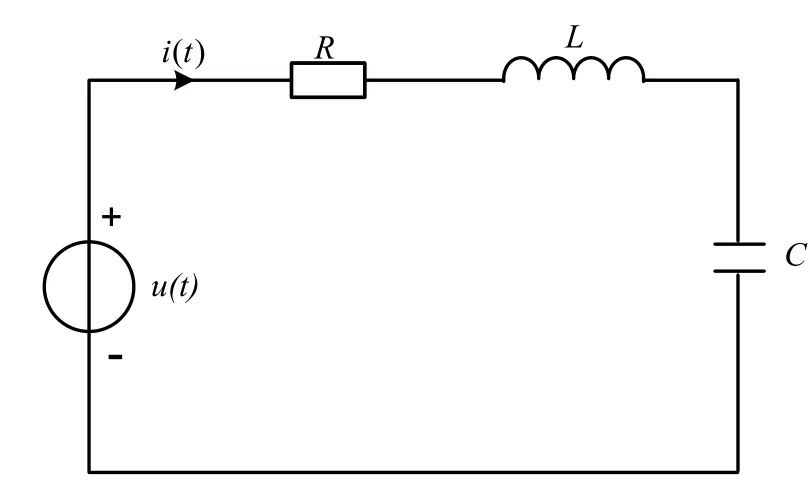
图5 时域电路图

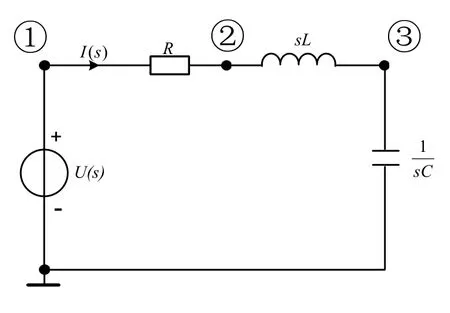
图6 S域电路图

RLC时域电路以及其在S域下的电路模型分别如图5和图6所示。使用改进节点法处理图6电路生成的代数方程组TX=B为：

其中，Vn1、Vn2、Vn3为节点电压，I(s)为流出电压源的电流，s为拉普拉斯变换符号。由于生成的代数方程组中，含有符号变量s，所以需要使用具有符号运算功能的工具进行求解。

2.3 代数方程组的求解与状态方程的提取

使用改进节点法生成代数方程组TX=B后，应使用具有符号运算功能的工具求解代数方程组。本文在MATLAB平台上对算法进行了实现，MATLAB具有强大符号运算功能。当将代数方程组TX=B求解完成后，解向量X为节点电压和非第一类元件支路电流的拉普拉斯变换表达式。由使用者确定电路系统激励和响应，根据已求出的解向量，求出系统激励和响应的拉普拉斯变换表达式，再根据式(12)求出单输入——单输出系统的传递函数。

假设得到的系统传递函数为：

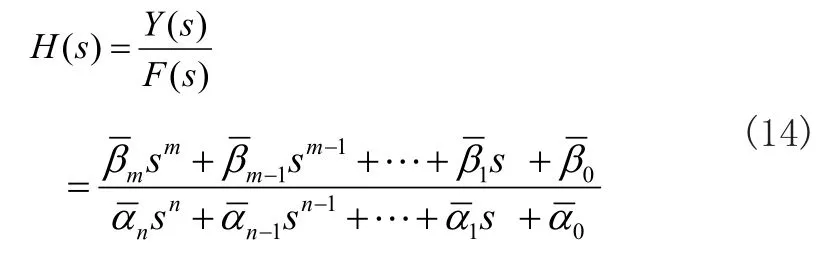
使用符号运算，分别将传递函数分子多项式Y(s)、分母多项式F(s)的系数向量提取出来，其中有：

因此：

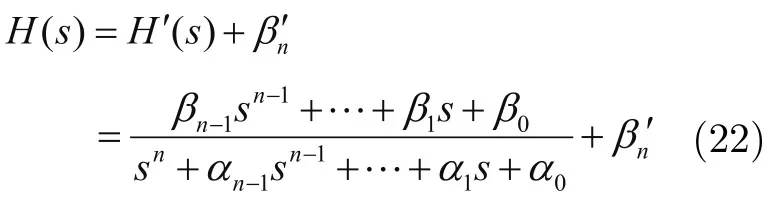
3 算例与分析

本文使用上述方法在MATLAB平台上实现了状态空间模型提取系统。图7为提取系统的运行界面，该系统采用固定格式的描述文件对电路网络进行描述。图8为提取系统的运行流程图，该系统读取电路网络描述文件进行分析，求解出系统传递函数，通过传递函数提取出电路系统的能控规范形实现和能观规范形实现的系数矩阵。下面通过算例来说明如何使用该系统提取出状态空间模型。

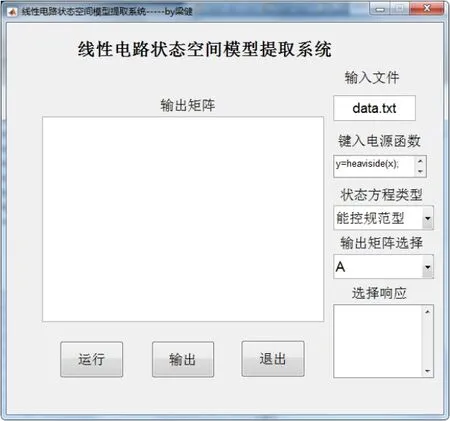
图7 系统运行界面

图8 提取系统运行流程

图9所示的算例电路较为复杂，元件E、H和G分别表示受控源VCVS、CCVS和VCCS，其传递函数较难直接求取，从而影响了状态空间模型的生成。电路中包含着受控源、纯电容回路和纯电感割集，使用传统的图论提取方法较难提出状态方程[5]。使用提取系统对图9电路进行分析，填入电路拓扑描述文件和电源函数，点击“运行”按钮，便可生成代数方程组TX=B。使用符号运算求解代数方程组，得到所有节点电压、支路电压和支路电流的拉氏变换。

图9 算例电路（电源频率1Hz）

选取电压源电压作为激励，节点5的电压作为响应。节点5电压的拉氏变换为：

对式(25)进行反拉普拉斯变换，可得到节点5点电压时域函数的近似表示为：

根据式(26)所绘出节点5电压波形和使用Pspice软件对电路进行仿真的结果的对比如图10所示，其中Pspice在仿真过程中的最大步长为5ms。图中的误差曲线为，可以看出两条曲线基本一致，误差Δ保持在6×10-5以内，充分表明了所得到节点5电压的拉普拉斯变换表达式是正确无误的。

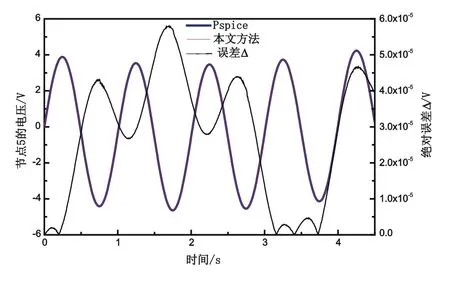
图10 节点5电压计算结果

图11 算例运行结果

根据传递函数和系统规范型实现的关系，由式(27)可得系统的能控规范型实现和能观规范型实现分别如式(28)和式(29)所示。在提取系统上，选择电压节点5作为响应，点击“输出”按钮，可得到算例运行结果如图11所示。图11中的输出矩阵为能控规范形实现的系数矩阵A。通过将式(28)的系数矩阵A与图11中的输出矩阵对比可知，提取系统的运行结果是准确可靠的。

4 结束语

本文提出了一种适用于线性电路系统的状态空间模型自动提取方法，能够提取出能控规范形和能观规范形两种基本的状态空间模型。该方法采用频域分析法和改进节点法，解决了复杂电路的传递函数难以直接求取的问题。在MATLAB平台上实现了提取系统，通过实例表明，该提取系统操作简单、运行结果准确可靠，为线性电路的分析提供了有力工具。