基于数字微流控生化检验操作调度的混合遗传算法研究
2018-10-11王鹤
王 鹤
(河南工程学院,郑州 451191)
0 引言
微流控生物芯片(即芯片实验室)的出现,推动生化分析检测向整体微型化、集成化、自动化与便携化方向迈出了一大步。样品和试剂的分配、输运、存储、混合、分离与检测等功能可以通过微流控生物芯片轻松地完成。试剂消耗小、成本低廉、检测灵敏度高以及重复使用等优势使其在生物医学、分析化学、药物诊断、食品安全以及环境监测等领域都有广泛的应用[1,2]。
与传统基于连续流的微流控生物芯片相比,数字微流控生物芯片不需要微阀、微泵等复杂的微结构,就能在二维阵列结构上独立地控制多个微液滴完成各种基本操作以实现相应的生化分析检测[3~6]。因此,数字微流控生物芯片具有可扩展、可动态重构的系统架构。然而,在许多实际应用中,往往要求不同类型的生化检验操作在同一个芯片上协同运作,这在一定程度上极大地增加了芯片系统的复杂性。而传统数字微流控生物芯片所采用的全定制设计制作技术扩展性差,而且2D电极阵列的尺寸(即资源约束)以及生化检测试验中各操作之间的功能依赖性(时序约束)均限制了片上并行操作的数量。以上各种问题的出现使得传统数字微流控生物芯片的全定制设计技术已经远不适用于大规模的生化分析与检测。因此,针对上述问题,参照超大规模集成电路(VSIA),在芯片系统中需要引入计算机辅助设计,可优化芯片结构,减少人为干预,提高芯片的利用率及效率[7~9]。
在生化检验分析中,生物样本对很多因素(如环境、温度等)都非常敏感,难以在片上保持最佳的临床(如床边检测)或实验室环境。所以,为了确保检验结果的完整性,在最终获得测定结果之前,要实现在满足目标和约束(包括资源约束和时序约束)的前提条件下,生化检验中各样本和试剂操作的并行处理达到最大化,进而减少样本液滴在芯片上的操作时间,以使生化检验完成时间最小化。因此,要实现上述目标的关键方法之一就是对数字微流控生物芯片进行架构级调度。因此,这里研究的数字微流控生化检验操作的调度问题,其实就是带有资源约束的项目调度问题。而以往学者对这方面的研究很多是将其按照单模式资源约束项目调度问题来分析处理的[7,10]。单模式资源约束项目调度问题是指项目中的每项任务只有一种执行模式,具有一组任务工期和资源需求。但是,生化检验中的各操作任务其实是具有多种执行模型的,比如,可以从2×2、2×3或2×4电极阵列混合器任选其一完成一个混合操作,那么在不同的电极阵列混合器上完成同一个混合操作就需要不同的资源需求量和完成时间。因此,当操作任务具有多种执行模式时,合理安排各个任务的执行模式,可大大节约资源,缩短完成时间。
本文将数字微流控生化检验操作的调度问题按照多模式资源源约束项目调度问题来分析,提出了利用双层混合遗传算法(DHGA)对数字微流控生化检验中液滴操作的时序调度进行优化。将关键链技术引入传统遗传算法中,在第一层算法确定液滴调度次序的基础上,采用关键链技术与第二层遗传算法相结合的方式,对芯片资源进行重新优化配置,使算法加速向最优解收敛,以达到生化检验完成时间最少的目标。
1 问题描述
数字微流控生化检验中,液滴操作步骤可以看作是一系列具有先后次序的操作,这一问题通过有向图模型进行描述,如图1所示。
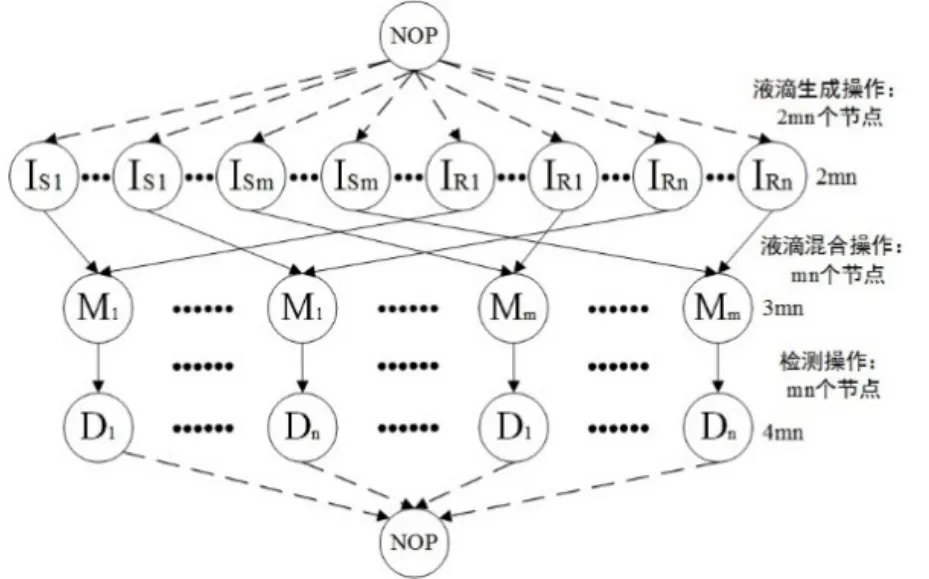
图1 多元生化检验有序图模型
在上述生化检验中,假设从芯片储液池需要生成m种样本液滴Si(i=1,2,…,m)和n种试剂液滴Rj(j=1,2,…,n),这里用I表示液滴生成操作。在后续操作中,为完成相应的酶化验,需要将m种样本液滴Si和n种试剂液滴Rj依次相互混合,那么样本液滴Si有n个生成操作,m种样本液滴就会有mn个生成操作;同理,n种试剂液滴Rj也有mn个生成操作,因此共有2mn个生成操作。液滴生成操作的时间主要由系统参数决定,而液体的流动特性对其几乎没有影响[11]。与m种样本液滴Si和n种试剂液滴Rj依次相互混合所对应的有mn个操作,而且1×4、2×2、2×3或2×4等多种不同类型的电极阵列混合器(即混合操作的执行模式)均可用于完成该操作。另外,对于各种试剂来说,在使用前往往都要用同一种液体对其进行高度稀释,因此,液滴混合时间主要由样本粘度和混合器类型决定。因此,可认为同一种样本与不同类型的试剂在同一类型混合器上完成混合操作的时间相同。注意,通常在生化检验中液滴混合操作之后往往都要进行液滴分离操作,因此这里液滴混合操作的完成时间均已包含液滴分离操作的时间。液滴混合之后,需要对其进行生化反应结果的检测,而酶测定的类型决定了光学检测时间。因此,在数字微流控生化检验液滴调度问题中共有K=4mn项操作任务,对各任务进行顺序编号。保证操作任务k(k=1,2,…,K)的编码大于它所有紧前操作的编码,并且任一操作k都必须从wj种执行模式中选择其一执行,执行过程中不允许中断或改变执行模式。不同的执行模式具有不同的资源需求和操作完成时间。这里的资源需求包含可重新配置的资源需求P和不可重新配置的固定资源需求Q。
图1是由与操作任务相对于的节点组成,各节点用vi(i=0,1,2,…,K,K+1)表示,其中设置了两个没有任何液滴操作的空节点NOP,即v0和vK+1。该有向图模型可用G(V,E)表示,节点集V={vi:i=0,1,2,…,K,K+1},边集E={(vi,vj):i,j=0,1,2,…,K,K+1}用来表示两个液滴操作的前后依赖关系。为每个节点均设置一个权重di,表示操作vi的持续时间。相比液滴生成、混合、检测等操作,液滴移动操作的时间极短,可忽略不计,因此有向图模型中两个节点之间的边权重设置为0。
2 数学模型
根据上述分析,生化检测调度问题可以看做是0-1整数线性规划问题,因此建立数学模型[7,12]如下所示:
设xi,j为二进制变量,则:

其中,1≤i≤K;1≤j≤M,M表示松弛时间因子,即为所有操作时隙数量总和。由于每个检测操作只能被调度一次,因此:
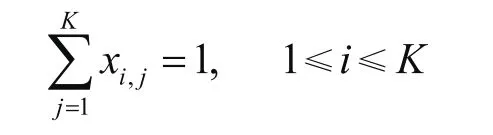
操作vi的开始时间si可以用一个变量x集{xi,1,xi,2,…,xi,m}表示。假设每个时隙长度为一个单位,那么操作vi的开始时间为:
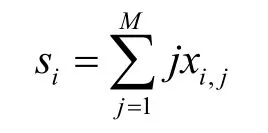
操作vi的持续时间为di,且操作vi和vi+1之间存在依赖关系,那么:

对于数字微流控生物芯片来说,除了上述的各操作间的依赖性这个时序约束以外,还有受芯片电极阵列尺寸限制的资源约束。这里假设每种液体的储液池数量Nr和每种酶测定的检测器数量Nd均设置为1,而且两者均属于不可重新配置的固定资源需求。于是对于m种样本和n种试剂有:

由于受资源约束的限制,有可能出现具有前后次序的两个操作无法被连续调度,这时就需要临时存储单元暂放液滴。而液滴存储单元和液滴混合器都属于可重新配置的资源需求。其中,用于液滴混合的电极数量设为Nmixer:
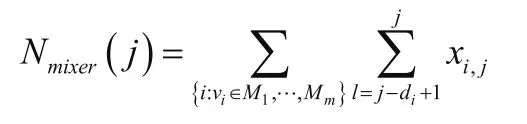
用于液滴临时存储的电极数量设为Nmemory:
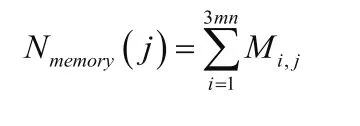
其中,Mi,j为一个二进制变量:

然而,数字微流控芯片尺寸大小固定,Nmixer和Nmemory之间是成反比的:

其中Ne的值取决于芯片尺寸。
因此,数字微流控生化检验液滴操作调度优化的目标就是生化检验完成时间最短:

在最大限度地利用并行性来完成生化检测的基础上,上述优化目标可转化为最小化最后一个操作的完成时间Tl,则优化目标转化为:
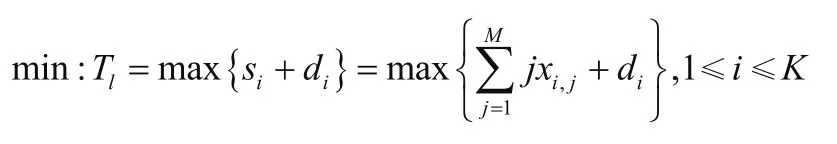
3 遗传算法设计
数字微流控生化检验液滴操作调度属于多模式资源约束项目调度问题,再加上具有两个不可重新配置的固定资源需求,因此,这是一个NP-complete问题。本文采用双层混合遗传算法来解决数字微流控生化检验液滴操作的调度问题。
在该算法中,第一层个体编码代表液滴操作调度次序,第二层个体编码代表在第一层确定的操作调度次序下的各操作执行模式。采用关键链技术对第二层个体进行进化,以替代第二层遗传算法的交叉过程;在既定的操作调度次序下求解各操作的最优执行模式以及与其相对应的适应度值,并将最优结果反馈给第一层遗传算法,再利用第一层个体的交叉、变异,不断迭代求出最优解。
3.1 第一层遗传算法
1)编码
针对多模式资源约束项目调度问题,本文采用双链表式编码[13]方式,即任务链表和模式链表两种链表:
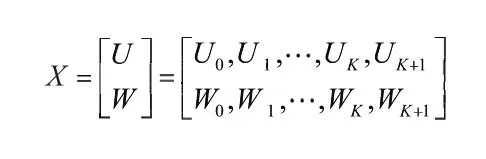
第一层个体编码为任务链表编码,液滴操作任务列表U=[U0,U1,···,UK,UK+1]表示满足时序约束的全部操作任务的一个排列次序,解码时各操作从左向右依次进行排列。这里要保证操作任务k(k=0,1,…,K,K+1)的编码大于它所有紧前操作的编码。
2)适应度函数
这里取第二层遗传算法的适应度函数的最优值作为第一层的适应度函数,即Fu=Fl*,其中Fl表示第二层适应度函数,其表达式参看3.2节。
3)选择
本文采用比例选择算子从当前代种群中选择出一些比较优良的个体,并将其复制到下一代种群中。在这种方法中,每个个体的选择概率与其适应度大小成比例。
4)交叉
对于传统的交叉算子来说,当随机选择的两条父串染色体相同时,算法会无法继续迭代进化,出现早熟收敛。为避免这一现象的出现,减弱对种群多样性的要求,第一层任务链表采用改进的交叉算子。假设随机选取两条父串染色体A和B,同为:(362794185),并随机产生两个交叉点,先将交叉段|7941|倒置变为|1497|,并将父串A的交叉倒置段|1497|移到父串B的尾部,将父串B的交叉倒置段|1497|移到父串A的首部,分别得到子串A1和B1,在此基础上,消去交叉段外与初始交叉段相同的基因,最终得到两条不同的子串A2和B2,具体如下所示:

如上分析可知,采用改进的交叉算子,即使随机选择的两条父串染色体相同,也能得到两条不同于父串的新染色体,而且两个子串染色体互相之间也不相同,这使得算法得以继续迭代进化,避免陷入局部最优解。
5)变异
物种变异几率很小,所以变异操作在遗传算法中只起辅助作用。操作任务链表中基因变异采用插入操作法,即对每代种群按照变异概率pm=0.03选中某个任务链表中的某一基因,分析得出该基因的所有紧前节点在该操作任务链表中的最后位置r1以及其所有紧后节点在任务链表中的最前位置r2,之后在r1和r2之间随机选择一个位置r,并将该基因置于位置r上[14]。
因此,第一层遗传算法的具体实施步骤如下:
(1)初始化两层控制参数;
(2)随机生成初始种群,产生N个个体Y1,Y2,…,YN。
(3)将每个个体Yi的值带入第二层遗传算法中得到对应的最优解Fl(Yi)*,并保存取得该最优解的第二层个体值。
(4)采用比例选择从当前代种群中选择出优良个体,并将其复制到下一代种群中。
(5)对第一层个体进行交叉变异,产生新一代个体,并计算其适应度值。
(6)判断新个体适应度是否满足终止条件。若满足,则算法的迭代过程收敛,算法结束;否则,转至(3)重复以上步骤。
3.2 第二层遗传算法
1)编码
第二层个体编码为模式链表编码,模式列表W=[W0,W1,…,WK,WK+1]表示根据任务列表中各操作对应的执行模式。操作vk(k=0,…,K+1)的执行模式有{1,2,…,wk}种,在满足资源约束的条件下,Wk∈[1,wk]随机选取。但是,由于操作v0与操作vK+1都是空操作,既不花费时间也不消耗资源,因此设置W0=WK+1={1}。
2)适应度函数
数字微流控生化检验液滴操作调度优化的目标是最小化最后一个操作的完成时间Tl,因此本层适应度函数定为Fl=1/Tl。
3)关键链技术对个体进化
这里对满足资源约束的全部个体都进行进化,因此进化概率设为1。如果资源需求总量不大于约束,则采用关键链技术对个体进化;否则,调整各操作任务的执行模型,直到满足资源约束为止。所谓的关键链技术对个体的进化,就是计算出所有关键链任务工作时系统的闲置资源,求出在满足资源约束的情况下,可缩短数字微流控生化检验完成时间的新执行模式,替换旧模式。新的完成时间应该满足:
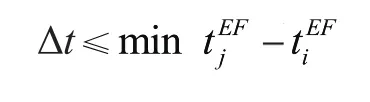
其中,tEFj表示操作i的紧后操作的紧前操作集合中各操作的最早结束时间。该公式保证了操作i在更新执行模式之后仍然处于关键链上。然而,如果没有任何操作的执行模式发生变化,那么任意选择c个操作(c为不大于4mn/3的随机整数)对其进行进化:(1)当中若有非关键链操作,则在资源消耗较少的执行模式中随机选取一种替换旧模式。当不可重新配置的固定资源Q紧张时,优先选取消耗Q较少的执行模式;反之,优先选取可重新配置的资源P消耗较少的执行模式。(2)当中若有关键链操作,则在满足资源约束的条件下,在完成时间较少的执行模式中随机选取一个替换。
4)变异
若进化过程中执行模式发生变化的液滴操作数量为0,或者出现随机概率大于变异概率,则任意选择z个操作(z为不大于mn的随机整数),在满足资源约束的情况下,随机更新它们的执行模型。第二层变异概率随迭代次数线性增加,有利于促进算法朝全局最优方向进化。
因此,第二层遗传算法的具体实施步骤如下:
(1)生成初始种群,产生N'个个体Y1',Y2',…,YN'。
(2)计算每个个体Yi'的适应度值,并进行评价:
(3)利用关键链技术对个体Yi'进行进化,替代交叉过程,并对其变异,计算出新个体的适应度值。
(4)判断新个体适应度是否满足终止条件。是则算法结束;否则,转至(3)重复以上步骤。
4 仿真结果及分析
为验证该算法的可靠性与有效性,采用文献[7]的实验数据进行仿真。表1给出了文献[7]中5种多元体液的检验数据,其中样本S1:血浆,S2:血清,S3:尿液,S4:唾液;生化检验A1:葡萄糖测定,A2:乳酸测定,A3:丙酮酸测定,A4:谷氨酸测定;Mi表示样本Si与某试剂的混合操作;Di表示生化检验Ai对应的观测操作。但是,文献[7]是将生化检验液滴操作调度问题按单模式资源约束项目调度问题来处理的,即每种液滴操作只有一种固定执行模型;采用M-LS算法和遗传算法(GA)两种启发式算法分别对上述4种测定实验进行了计算。
在生化检验中,同一混合操作在不同尺寸的混合阵列(即不同的执行模式)上完成,其完成时间不同。假设多元体液检验在不同混合器上完成混合操作的时间[15]如表2所示,而且文献[7]中各样本均是在1×4阵列混合器上完成混合操作的。由表2可知,通常情况下混合器尺寸越大,混合操作完成时间越短;电极单元数量相同时,线性混合器(如1×4)比多行阵列混合器(如2×2)完成混合操作的时间短。因此,混合器类型的选择是影响数字微流控生化检验完成时间的一个重要因素。当然,液滴生成器、试剂稀释器等也与混合器类似。
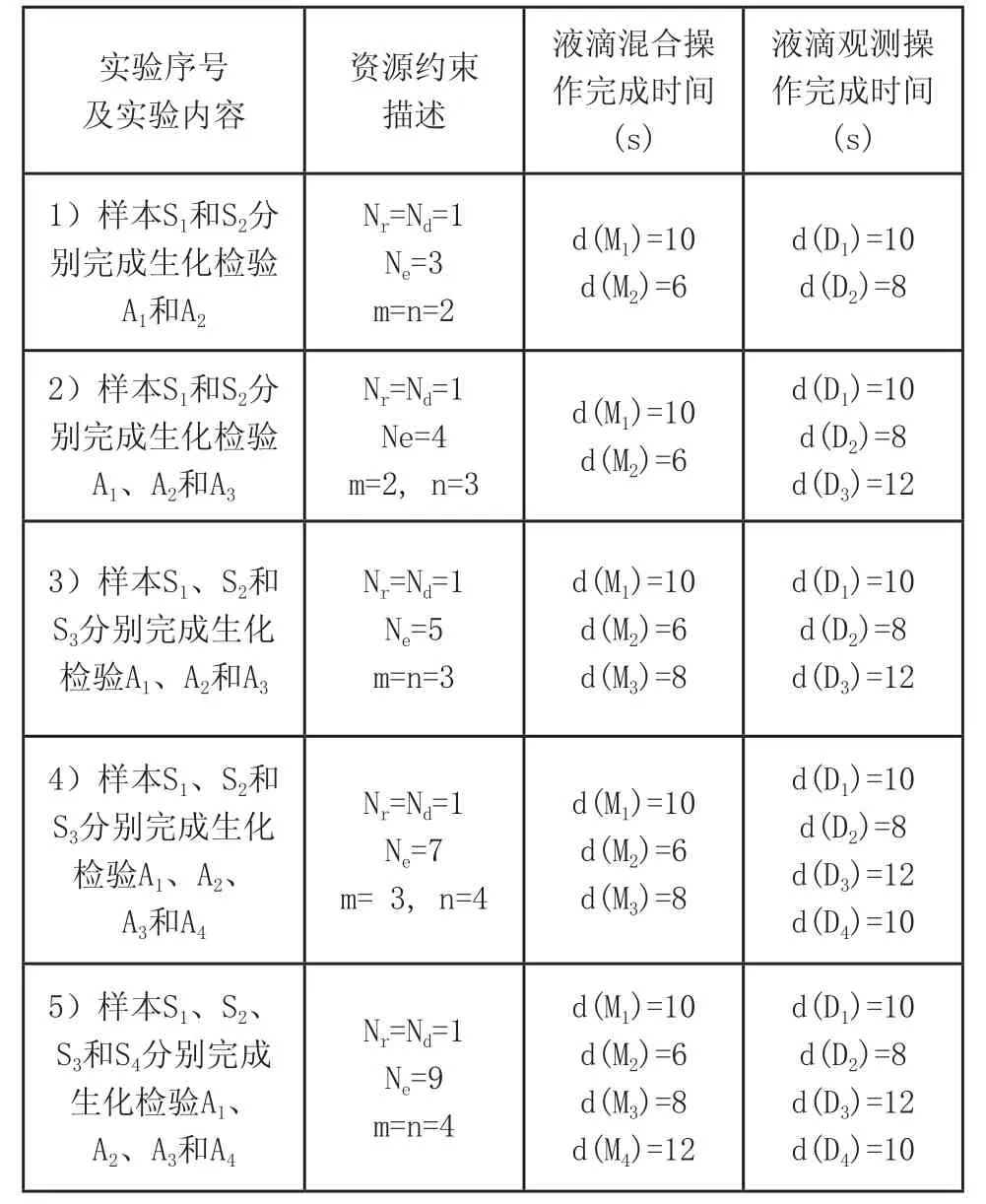
表1 实验数据

表2 样本在各种混合器上完成混合操作所需时间 (单位:s)
双层混合遗传算法主要参数初始化如下所示:

图3给出了双层混合遗传算法和文献[7]使用算法之间仿真结果的对比。从结果可知,双层混合遗传算法从解的质量和计算时间来看,均具有显著优势,几乎都达到了解的下限,而且计算时间较短。

表3 生化检验完成时间结果对比 (单位:s)
5 结论
数字微流控生化检验液滴操作调度问题属于多模式资源约束项目调度问题。通过采用双层混合遗传算法对液滴操作的时序调度进行优化;将关键链技术引入遗传算法中,在第一层算法确定液滴调度次序的基础上,采用关键链技术与第二层遗传算法结合的方式,对芯片资源进行重新优化配置,使算法加速向最优解收敛。由该算法得到的解几乎都达到了解的下限,因此缩短了生化检验完成时间,同时减少了计算时间。仿真结果表明了算法的有效性和可行性,对数字微流控生化检验液滴调度优化具有一定的参考价值。
