高校初等数论课程概念教学探讨——以小学教育专业为例

2018-10-11李玉慧

天中学刊 2018年5期

李玉慧

李玉慧

（怀化学院教育科学学院，湖南怀化 418000）

初等数论是小学教育专业的一门专业主干课程，其概念的教学十分重要。为了充分提高教学效果，在此课程的教学中，教师应精讲关键概念的定义，细讲关键概念的性质，注重相似概念之间的对比，帮助学生把关键概念同其他概念联系起来形成概念体系，并让学生通过足量的应用性练习深刻理解概念。

小学教育专业；初等数论；概念；教学；思考

一、小学教育专业开设初等数论课程的必要性

初等数论是一门古老的数学基础学科，主要研究整数的基本性质，其理论和方法已广泛应用于现代密码学、算子理论、最优设计、组合代数及信息科学等诸多领域[1]217。我国师范院校一般都设有小学教育专业，而几乎所有的小学教育专业都开设有初等数论课程。初等数论课程的教学内容主要是整数的性质及其应用，例如整除、公约数、公倍数、质数、合数、同余的性质及应用等，这些内容大部分与小学数学的教学重点相吻合。可见，小学教育专业开设初等数论课程有利于提高学生的数学素养及小学数学教学能力。

湖南省规定2016年1月1日及以后入学的全日制师范教育类专业学生，必须参加国家统一组织的中小学教师资格考试并获得教育部考试中心颁发的中小学教师资格考试合格证明，才能申请教师资格证书。而按照2012年5月教育部考试中心和教育部师范教育司联合下发的《中小学和幼儿园教师资格考试大纲（试行）》“综合素质”考试目标要求，中小学和幼儿园教师应“具有阅读理解、语言表达、逻辑推理、信息处理等基本能力”，并在逻辑推理能力方面提出了较高的要求，即能够准确而有条理地进行推理、论证。因为初等数论课程能够有效地训练学生的思维，提高其逻辑推理能力，所以小学教育专业开设初等数论课程有利于学生顺利通过国家教师资格考试。

数论的很多命题看似十分简单，但一些命题的证明难度极大，例如角谷猜想、哥德巴赫猜想至今还未被证明。中外许多数学家都是被数论问题所吸引而对数学产生浓厚兴趣的。学生在学习初等数论的过程中，很多结论和现象（如质数螺旋现象等）可以由自己独立地认识理解，很多具有创造性的简单问题可以由自己独立地解答，这不仅可以激发其学习兴趣，而且可以培养提高其观察力、创造力。

二、初等数论课程概念教学的重要性

数学是研究现实世界中数量关系和空间形式的一门科学，因而数学概念是客观世界中数量关系和空间形式的本质属性在人们头脑中的反映，它是用数学语言和符号揭示事物共同属性的思维形式。概念反映的所有对象的共同属性的总和称为这个概念的内涵，而适合这个概念所指的对象的全体称为这个概念的外延。数学中的概念是多种多样的，根据它们的具体内容和在数学中的地位和作用，就有基本的关键概念和一般的次要概念之分[2]74。以下把初等数论中的整除、同余等概念称为关键概念，把亏数、完全数、盈数等概念称为次要概念。

数学概念是数学基础知识的重要组成部分，是学习其他数学知识的基础，也是进行正确计算、判断、推理的依据，因此概念教学有利于培养学生的逻辑思维能力，发展学生的智力，而学生对概念的掌握程度直接关系到课程学习的好坏。

小学教育专业数学类课程的设置目标是培养合格的小学数学教师。小学数学中与数的运算有关的概念共有64个[3]，但去掉分数、小数的定义和数的加减乘除四则运算相关的定义后，几乎全部包含在初等数论中，所以学生掌握初等数论的各个概念能够为小学数学教学打下良好的基础。

小学教育专业初等数论课程中的数学概念较多，但学生学习此课程前对其中的绝大部分都有一定的了解，所以一些教师在教学中常常会“轻概念、重推理”。逻辑推理是初等数论教学的重点无可厚非，但轻概念就值得商榷了。笔者曾选取数位、整除、约数、质数等10个概念，在怀化学院2013级小学教育专业数理方向‍①的学生中做了一次调查，结果表明所有学生都学过这些概念，但多数学生不能准确表述，部分学生因对一些概念的理解比较模糊而导致错误的看法。加强初等数论课程概念教学的必要性和重要性由此可见。

三、小学教育专业初等数论课程概念教学的策略

（一）精讲关键概念的定义

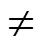
（二）细讲关键概念的性质

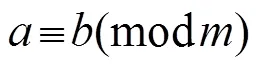
（三）把关键概念与其他概念联系起来形成概念体系

初等数论中的很多概念都是上下位关系，而关键概念一般为上位概念，如整除是约数的上位概念，而约数是公约数的上位概念，公约数又是最大公约数的上位概念。在初等数论课程的教学中，教师应以关键概念为基础，通过上下位关系将若干概念联系起来形成概念体系，例如，可将整除理论中的整除、倍数、公倍数、最小公倍数、约数、公约数、最大公约数、合数、质数、质因数、分解质因数、互质、两两互质、亏数、盈数、完全数等概念组成一个概念体系。形成概念体系能使数学知识系统化、条理化，有效避免相似概念的混淆。学生只有了解概念体系中各个概念所处的位置及相互联系，才能比较全面、深刻地理解相关概念。教师在帮助学生形成概念体系时，应有意识地引导学生去对比容易混淆的概念，防止产生负迁移。

（四）把初等数论的概念与已学课程中的类似概念做对比讲解

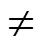
（五）要求学生多做与概念相关的练习

应用概念是学习概念的重要目的，也是牢固掌握概念的必由之路。在初等数论课程的教学中，教师应适时地多布置一些与概念相关的练习，并注意选择巧妙地插入数学概念的题目，使学生在运算、推理、证明的过程中领悟数学概念的理论指导作用，逐步提高概念思维能力。例如质数与合数的概念十分简单，理解起来难度也不大，但学生只有通过一定量的应用性练习才能深刻理解和真正掌握，而判断某个具体的数为质数或合数多是从概念的定义出发的，如可根据质数与合数的定义用反证法证明质数的个数为无限个。

小学教育专业初等数论课程的概念教学十分重要，但在保证学生掌握概念的前提下，培养学生的逻辑推理能力也是该课程教学的一个重要目的。教师在进行概念教学时，必须把握概念教学的目标，正确处理概念教学的发展性与阶段性矛盾，必须加强直观教学，处理好具体与抽象的矛盾。