不用单位“1”如何解分数应用题——新加坡教材中分数应用题的解决

◇罗永军

新加坡小学数学教育在国际上一直保持领先水准，位居国际权威测试PISA和TIMSS排行榜的前列，最近的一次测试在2015年，新加坡更是获得了双料冠军。

近来因工作原因，较多地接触了新加坡数学，在笔者手头上有两种在新加坡发行量较大的教材，一种是 My Pals Are Here（3rd Edition）[1]（以下简称教材 1），另一种是Targeting Mathematics[2]（以下简称教材 2），这两种教材的编排结构和内容大体相同，不同的地方在于素材选用方面各有特色。与其他各国相比，新加坡的数学教材无论是编排结构还是教学内容都是与我国现行教材最接近的。不过，具体到某些知识点时，处理方法还是有明显不同，比如分数应用题（新加坡教材中称为文字题）。

在小学数学中，分数应用题因其抽象程度高、范式变化多，而又很难与现实生活、学生经验接轨，所以学生往往难掌握，是小学数学的难点之一。新加坡教材在编排分数应用题时用到了一种称之为长条图（Bar Model）的思维工具，我们在教学时发现学生容易掌握，解决问题成效明显。

让我们先来看看下面这个问题（选自教材2）：

1.我国现行教材常用的方法。

也可以把分率转换成以总人数为单位“1”。

应用上述方法的关键是找准单位“1”。什么是单位“1”？人教版教材五年级下册（2012年版）中的说明是：“一个物体、一个计量单位或是一些物体等都可以看作一个整体。把这个整体平均分成若干份，这样的一份或几份数都可以用分数来表示。一个整体可以用自然数1来表示，我们通常把它叫作单位‘1’。”单位“1”是一个高度概括化的名词，不是一个具体数量又能表示一个具体数量。学生对单位“1”的领悟个体差异非常大，有不少学生到小学毕业还难以理解。既然学生对单位“1”的理解困难，为什么我们还要用这个方法来解决分数应用题呢？这是因为我们的教材在定义分数时是以单位“1”为基础，因此，以单位“1”为核心的解题方法也是顺理成章的。

不过，分数作为一个复杂的概念，其意义非常丰富，国内外许多学者都对分数的意义进行了深入细致的研究。比如（张奠宙，2010[3]）：

定义1（分数定义）：分数是把一个单位平均分成若干份，其中的一份或几份。

定义2（商定义）：分数是两个整数相除的商。其中除数不为0。

定义 3（比定义）：分数是 q与 p之比。其中p≠0.

定义 4（公理化定义）：有序的整数对（p，q），其中 p≠0。

除了基于单位“1”的理解，新加坡数学教材采用了“比的定义”，即把分数“整数化”。

2.新加坡教材呈现的方法。

新加坡教材把“分数”看成“比”，把分数应用题转换成整数应用题。如何转换呢？同样是上题中的两个分数 “女听众人数是总人数的教材中把它转换成总人数7份，其中女人占3份，剩余4份；“男听众人数是剩下人数的转换成剩余人数中男人占3份，儿童占1份。在转换过程中把份数用一种称为Bar Model的长方形条形图表示（如图1）。

图1

根据条件“男人比儿童多42人”在长条图中找到这两者关系，可以看出 “男人比儿童多2份”。由此可以先求出1份，再求出总人数7份，得：42÷（3-1）×7=147（人）。

3.新方法带给我们的启示。

上面两种方法是两种不同的思维起点，前者把分数看成一个“平均分”的结果，是一个数，注重部分与整体的关系。因此要先找到这个整体即单位“1”，求出单位“1”的对应数量，再求出几分之几的对应数量。后者把分数看作两个数的比，由两个数组成，把比的前项(分子)和后项(分母)分别用长方形的块数表示，每1块表示1份。然后根据条件先求出1份量，再求几份量。在这个“整数化”过程中，长条图作为一种思维工具，把思维过程以直观的方式固化了，并且作为一个基本单位参与数量的运算。

那么，这样的方法是否具有普适性？上面的例子中2个分数所表示的份数“凑巧”能够互联，如果是一般的情况呢？让我们看看下面这个问题（选自教材 1，如图2）。

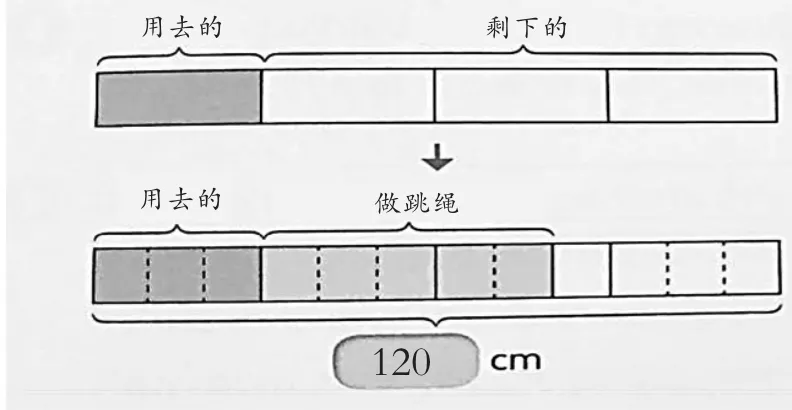
图2

根据题意先画出长条图，找到相应长条和数量的对应，可以求出：

每份长：120÷12=10（cm）。

剩下部分是：10×4=40（cm）。

平均分每段长是：40÷8=5（cm）。每段长5cm。

与上一题不同，本题中第一次用去后剩余部分无法直接分配，需要再次细分，但通过转换还是能将“分数整数化”。当然这样的转化也需要有铺垫，教材中安排了相应的例题（选自教材1）专门来学习转化。（如图3）

图3

（1）花在DVD上的钱是他收入的几分之几？

（2）花在汗衫上的钱是他收入的几分之几？

从上面新加坡教材处理较复杂的分数应用题的例题来看，“分数整数化”和长条图两者是相辅相成。“分数整数化”给长条图提供了绘制依据，而长条图则直观地表示了份数之间的关系，形象、具体地反映了数量之间关系，实质上是一种算术思维。与新加坡教材类似，我国浙教版（2010年版）教材也呈现过“分数整数化”编排。（如图4）

就此编排原因，笔者请教了该教材主编张天孝先生，他的回答是：“学了‘比’之后，应该将分数与比建立联系，并且进一步还可以与‘正比例关系’建立联系。”

图4

北师大版（2010年版）教材也有长条图，但作用与线段图是一样的，都表示分数的部分与整体关系，即单位“1”与分率的关系，如图5：

图5

在此基础上，根据分率与单位“1”的关系列出方程或算式，用代数方法来解决，是一种代数思维。

新加坡教材对于分数应用题的处理方法采用“分数整数化”和长条图相结合的编排方式，很有特色。不过，对它的介绍并不意味着笔者想肯定这是一种“好”或“不好”的方法。事实上，思维存在着多样性，具有很强的个人倾向性，不同的人对同一问题就算是思维方向一致也会有不同的思维路径。因此，我们老师的目标应该是扩展学生的思维，创造机会让学生感受不同的思维形式或思维辅助手段。