层层猜想 处处探究——“三角形的拼接”教学实录与评析

◇执教/陈加仓 评析/符玲利

一、谈话引入，提出问题

1.谈话引入。

师：（呈现图片。图片略）大家玩过“桥梁建筑师”游戏吗？它是用什么图形来建造桥梁的？

生：三角形。

师：是的，三角形具有稳定性，用一个个三角形拼接成的桥梁，肯定比较牢固。今天这节课我们就来研究“三角形的拼接”。

2.提出问题。

师：猜一猜，10个三角形拼接，有14个连接点，有几条边呢？

生：30条边。

生：25条边。

生：5条边。

（师引导后，学生发现错误）

师：到底有几条边呢？一下子解决10个三角形的拼接问题有点困难，怎么办呢？

生：从2个三角形拼接开始研究。

师：真厉害，把复杂的问题简单化。

评析：通过“桥梁建筑师”游戏情境的导入，激发学生研究三角形拼接问题的兴趣，进一步感悟数学来源于生活。通过“猜一猜”的环节，学生感受解决10个三角形拼接问题的困难，从而进行简化渗透“化繁为简”的数学思想。

二、探索研究，发现规律

（一）举例。

1.2个三角形的拼接。

师：2个三角形是怎样拼接的呢？请同学们到黑板前演示一下。

学生板演“拼接”，课件再呈现结果。（如图1）

图1

师：数数看，它们分别有几条边、几个点呢？

学生回答后教师板书如表1。

表1

师：它们拼接的方法不同，得到的拼接图也不同，边数与点数也不同。请同学们仔细观察，它们有什么相同的地方？

生：都是2个三角形的拼接。

生：边数减少1，点数减少1。

生：边数比点数多1。

师：如果3个三角形拼接，边数与点数又有什么关系呢？请同学们自己画图研究。

2.3个三角形的拼接。

画图研究，汇报交流。

生：如图2，我把3个三角形拼接在一起，它一共有 9条边，7个点。（如图2）

图2

生：我研究的结果也是9条边，7个点，但是形状不一样。（如图3）

图3

师：为什么拼接形状不同，但是边数与点数却是相同的？

生：它们的拼接方式是一样的，都是点与点的拼接。

师：真棒！如果拼接方式不同，得到结果也不同。还有谁研究的结果不一样？

生：我是这样拼接的，（如图4）得到的边数是8条，点有6个。

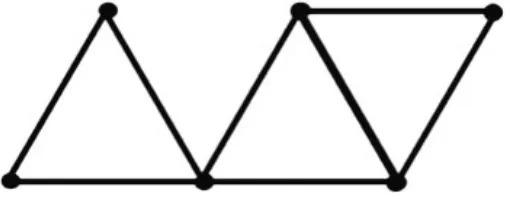
图4

生：我是这样拼接的，（如图5）得到的边数是7条，点有5个。

图5

课件展示学生的研究成果并补充在表1中。

师：请再仔细观察，3个三角形拼接时，边数与点数有什么关系？

生：边数比点数大2。

评析：动手操作可以激发学生的学习兴趣，促进学生理解与记忆，是活动经验积累的必备步骤。陈老师此处给学生充分的操作机会，反馈时注重引导学生比较相同数据、不同的摆法，突出共性，为后续推理奠定了基础。

（二）猜想。

师：请大家猜想一下：4个三角形拼接，边数与点数相差几？

生：4个三角形拼接，边数与点数相差3。

师：5个三角形拼接呢？

生：5个三角形拼接，边数与点数相差4。

生：相差数都比三角形个数少1。

师：也就是说“三角形个数-1=边数-点数（相差数）”，这样的猜想对吗？请同学们再动手验证一下。

评析：猜想是归纳推理过程中关键的一步，有了猜想学生才有进一步探究验证的必要性。教学中引导学生根据观察结果大胆猜想，有利于培养学生的创新思维能力。

（三）验证。

学生画图验证，汇报后补充在表1中，形成表2。

表2

师：通过刚才的研究，我们发现了“三角形个数-1=边数-点数”是正确的。

师：以此类推，6个三角形拼接，边数与点数相差几？（生：相差 5）7 个三角形拼接呢？（生：相差 6）8个三角形拼接呢？（生：相差 7）那么 10个三角形拼接，有 14个点，有几条边？（生：10-1=9，14+9=23）100个三角形拼接，边数与点数相差几呢？

生：相差 99。

生：不管几个三角形，它们的相差数总比三角形个数少1。

师：那我用字母n来表示任意个三角形，再增加1个三角形之后边数、点数会发生什么变化呢？

观察课件演示，找出边与点的增加数。（如图6）

图6

（2）观察发现增加的边数与点数之间的关系，如表3。

表3

生：三角形个数增加1，边数与点数的相差数也大了1。

师：三角形的拼接，我们已经研究好了，接下来，你们还想研究哪些图形的拼接呢？

生：正方形、五边形、六边形……

师：由于时间关系，这节课我们先研究正方形的拼接，那么怎么研究呢？

生：我们可以先举例研究，然后猜想，最后验证。

评析：为了让学生充分体验归纳推理的过程，陈老师先带领学生进行举例验证，但受课堂教学时间和数据的限制，总是不能穷举。于是通过n个与（n+1）个的图形直观操作，进一步进行验证，让学生经历完整的推理过程。

三、再次实践，拓展延伸

1.研究正方形的拼接问题。

学生动手画，观察，然后汇报。

生：我们发现“正方形个数-1=边数-点数”。

2.类推：五边形、六边形拼接，它们的个数与边数、点数之间的关系。

生：五边形个数-1=边数-点数。

生：六边形个数-1=边数-点数。

生：八边形个数-1=边数-点数。

师：谁能归纳概括一下这些规律？

生：多边形个数-1=边数-点数。

师：三角形的拼接存在这样的关系，为什么其他多边形的拼接也存在这样的规律呢？

3.解释原因，沟通联系。

课件演示如图7后，指出：正方形、五边形、六边形等多边形的拼接都可以转化成三角形的拼接。

图7

评析：在探究三角形拼接问题的过程中，学生初步掌握了推理的方法。于是陈老师立即引导学生用归纳推理的一般方法研究四边形中各个量之间的关系,再顺势引导：为什么四边形、五边形、六边形也会有这样的规律呢？通过课件演示图形分割，学生顿时豁然开朗。此环节猜想与证明相结合，让归纳推理更具科学性。

四、欣赏总结，课外探索

1.课件演示各种拼接图形。

2.课外探索：课件演示，利用下列各拼接图，拼接成立体图形，则面数、棱数与点数又有什么关系呢？（如图8）

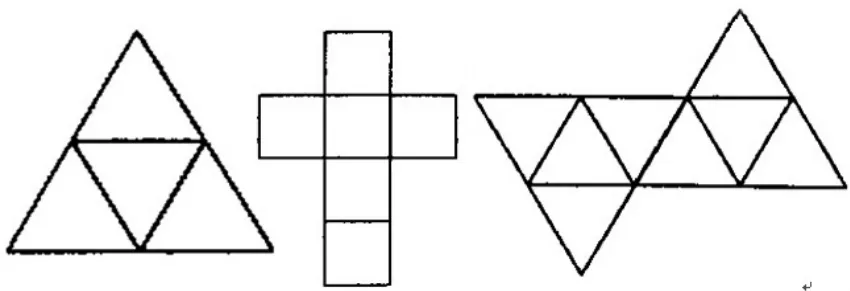
图8

评析：课的结尾欣赏完各类图的拼接后，提出新的数学问题：“立体图形中面数、棱数、点数之间又有什么关系呢？”这为学生后续的研究指明了方向。从平面图形的研究到立体图形的研究，陈老师不仅教给学生知识、方法，还培养学生的推理意识和能力。