一类随机波动方程的渐近行为

班爱玲

(池州学院 数学与计算机学院，安徽 池州 247000)

关键字：强阻尼；波动方程；随机吸引子；Wiener过程

引 言

设U⊂R3是具有光滑边界∂U的有界开集，考虑下面具有临界增长指数的强阻尼随机波动方程的初边值问题：

(1)

其中u=u(x,t)是U×[0,+)上的实值函数，α>0为强阻尼系数，β>0为阻尼系数，K>0为耗散系数，非线性项f∈C′(R;R)具有临界增长指数，W(t)是一完备概率空间上的一维双边Wiener过程。

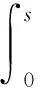
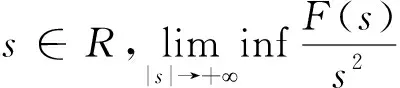
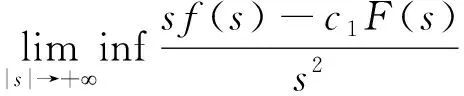
(III)存在常数c2>0，0p4,∀s∈R，使得|f′(s)|c2(1+|s|p)。

当W(t)≡t时，方程(1)是一个无白噪音的确定性系统，很多作者都研究了其方程的全局吸引子的存在性及全局吸引子的Hausdorff维数估计，见[1,2,3]。然而相比确定性动力系统，随机动力系统更能准确地描述客观现象，如流体力学中极其重要的随机Navier-Stokes方程，如受自然界风影响的水流等。

方程(1)具有实际的物理意义，如量子力学中非线性项f(u)=|u|γu,γ≥0的波动方程，又如f(u)=sinu的Sine-Gordon方程，见[4,5,6]，而本文主要证明对非线性项f(u)具有临界增长指数的条件下方程(1)的解所确定的随机动力系统存在一个紧的随机吸引子。

1 预备知识

设(Ω,F,P)为一完备的概率空间，Ω={ω∈C(R,R):ω(0)=0}，Ω上的Borelσ-代数F是由紧开

拓扑生成的，P是F上的Wiener测度，定义Ω上的一簇保测的与遍历的变换{θt,t∈R}如下：

θtω(·)=ω(·+t)-ω(t),t∈R。

则(Ω,F,P，(θt)t∈R)成为遍历的度量动力系统。

定义1.1[7]设(Ω,F,P，(θt)t∈R)是一个度量动力系统，X是一完备的可分空间。若(B(R+)×F×B(X),B(X))-可测映照φ:R+×Ω×X→X,(t,ω,x)→φ(t,ω,x)，满足条件：

(1)φ(0,ω,x)=x,ω∈Ω,x∈X;

(2)φ(t+s,ω,·)=φ(t,θsω,φ(s,ω,·)),s,t≥0,ω∈Ω;

(3)φ关于t和x连续，

则称φ是(Ω,F,P，(θt)t∈R)上的一个连续随机动力系统。

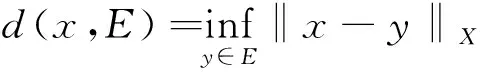
dH(E,F)称为从E到F的Hausdorff半距离。

定义1.2[7](1)若映照ω→d(x,D(ω))对任意x∈X是可测的，则集值映照ω→D(ω):Ω→2X称为随机集。若任意ω∈Ω,D(ω)是闭(紧)的，则ω→D(ω)称为随机闭(紧)集。若存在x0∈X和随机变量R(ω)>0使得

D(ω)⊂{x∈X:‖x-x0‖XR(ω)},ω∈Ω成立，则随机集ω→D(ω)称为有界的。

(2)若对p.a.s(依概率)ω∈Ω，

则称随机集ω→D(ω)是缓增的。

(3)若对任意的缓增随机集ω→D(ω)，存在t0(ω)>0，使得φ(t,θ-tω,D(θ-tω))⊂B(ω),t≥t0(ω),ω∈Ω成立，则ω→B(ω)称为随机吸收集。

(4)若对任意的缓增随机集ω→D(ω)，有

则ω→B1(ω)称为随机吸引集。

(5)若随机紧的吸引集ω→κ(ω)满足φ(t,ω,κ(ω))=κ(θtω),ω∈Ω,t≥0，则称ω→κ(ω)为随机吸引子。

定理1.1[7]设φ是(Ω,F,P，(θt)t∈R)上的连续随机动力系统，若φ具有一个缓增随机紧吸引集ω→B1(ω)，则φ具有唯一的随机吸引子ω→κ(ω)，满足

本文中用到的一些记号如下：

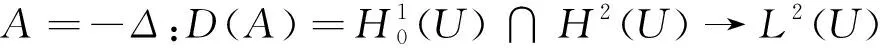
0<λ1λ2…λl…,λi→+(i→+)。

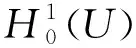
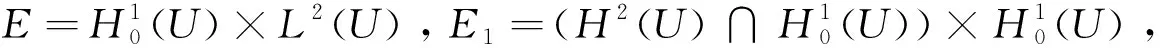
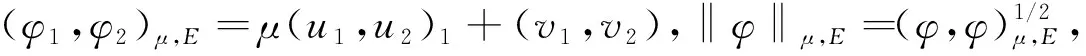
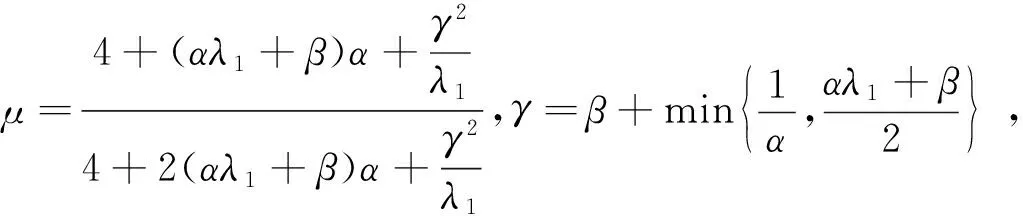
易证‖.‖μ,E等价于E的通常范数。

2 主要结果

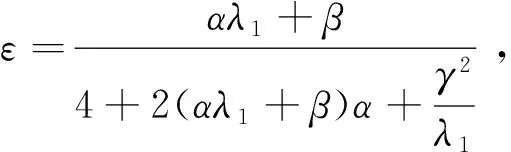
则方程(1)可以化为以下初值问题：

φt+Λ(φ)=Q(ω,φ),φ0(ω)=(u0,u1+εu0)T,t>0，

(2)

其中

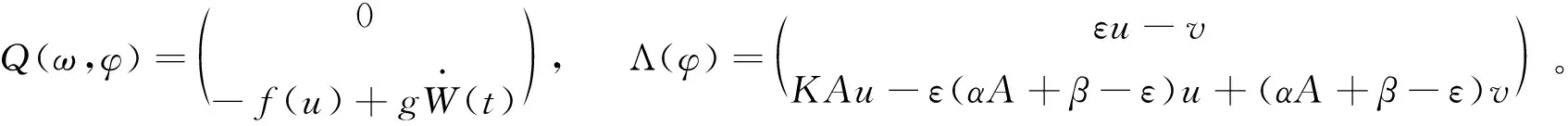
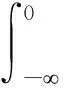
显然，随机变量z(ω)是缓增的，映照t→z(θtω)是p.a.sω∈Ω连续的，参考[8,9]。

令h(t)=v(t)-gz(θtω)，由方程(2)可得，

(3)

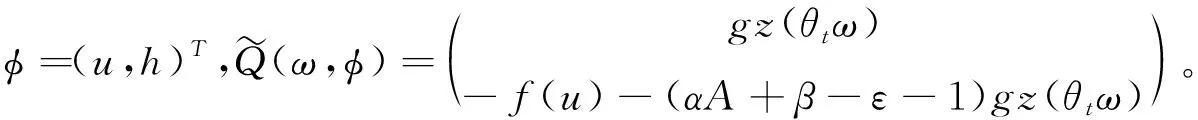
方程(3)中的算子Λ是E上的一个扇形算子并生成E上的一个解析半群{eΛt}t≥0，

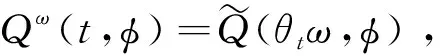
引理2.1[10,11]对任意ω∈Ω,φ0∈E，方程(3)存在唯一的φ(·,ω,φ0)∈([0,+),E)，

使得φ(0,ω,φ0)=φ0以及φ(t,ω,φ0)满足：

(4)

若φ0∈D(Λ)，则存在φ(·,ω,φ0)∈C([0,+);D(Λ))∩C1((0,+);E)满足(4)，并且

φ(t,ω,φ0)关于t,φ0二元连续，所以φ:R+×Ω×E→E是一个连续的随机动力系统。

为下文研究方便，引入两个同构映照：

Sε(θtω):(x1,x2)T→(x1,x2-εx1+gz(θtω))T;Tε:(x1,x2)T→(x1,x2-εx1)T。

其逆同构映照分别为：

因此，讨论动力系统ψ(t,ω)，只需讨论与它等价的动力系统φ(t,ω)即可。

引理2.2[1]对任意φ=(u,v)T∈E1，

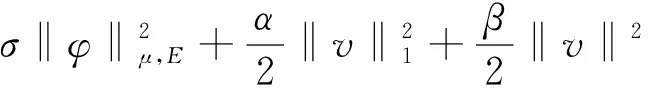
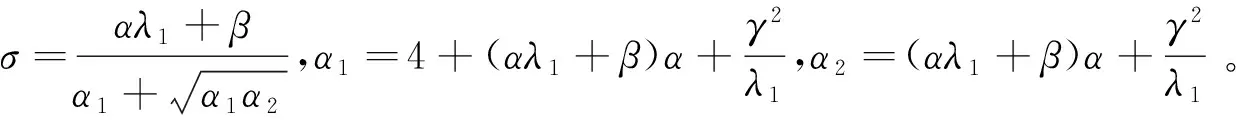
定理2.1设φ为方程(2)的一个解，则存在E中的一个缓增随机集B0(ω)，对E中任意的缓增随机集B(ω)，都存在一个缓增随机变量TB(ω)>0，使得

φ(t,θ-tω)B(θ-tω)⊂B0(ω),∀t≥TB(ω),ω∈Ω。

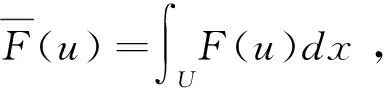
(5)

由条件(I)，(II)得，存在常数k1,k2≥0，使得

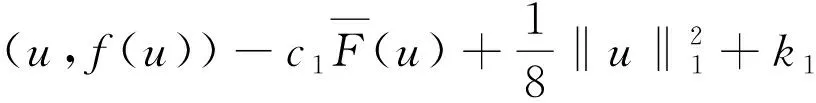
(6)

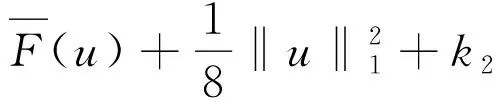
(7)

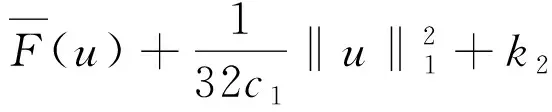
(8)

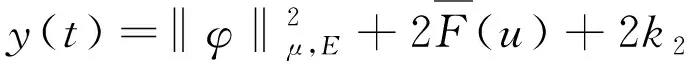
由引理3.2和(6),(8)得，

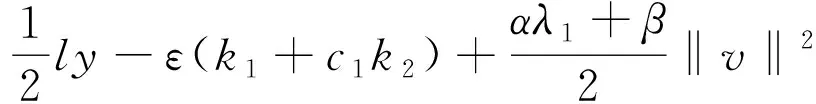
(9)

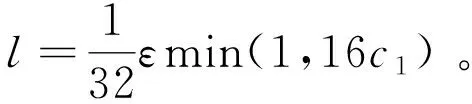
由(5),(9)得

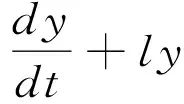
因此,由Gronwall不等式得，

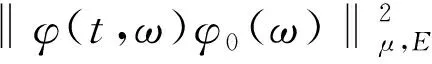
由(Ⅲ)知，存在常数c3>0，使得|f(u)|c3(1+|u|p+1)，对于任意的随机有界集B(ω)，由于φ0(ω)∈B(ω)是缓增的，则由⊂H-1(U)得，存在常数c4>0，使得c4，由(6)得，存在常数c5>0，使得c5，

因此，存在常数

由文献[12]得，对任意ϑ>0，则存在随机变量r:ΩR+，使得，

‖z(θtω)‖2eϑtr2(ω),∀t∈R,ω∈Ω。

(10)

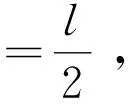
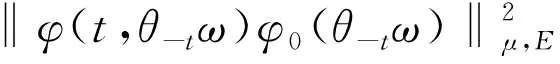
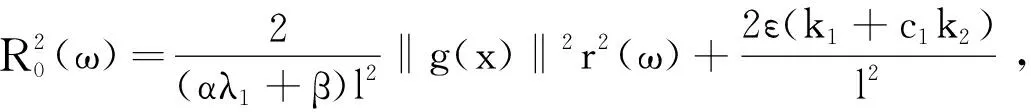
所以，B0(ω)=φ∈E:‖φ‖μ,ER0(ω)，则B0(ω)是φ(t,ω)的随机吸收集。

引理2.3对任意的缓增有界集B(ω)，设φ(t)为方程(2)的具有初值φ0=(u0,u1+εu0)∈B(θ-tω)的解，它可以分解成φ(t)=φξ(t)+φη(t)，其中φξ(t),φη(t)分别满足：

(11)

(12)

则当t→时，

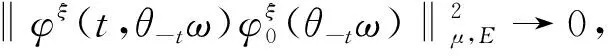
(13)

且存在一个缓增随机半径R1(ω)，使得对∀ω∈Ω，

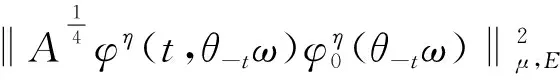
(14)

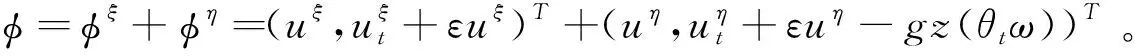
由(11),(12)得

(15)

(16)

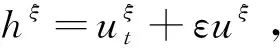
由引理2.2易推算得，当t→时，∀则(13)成立。

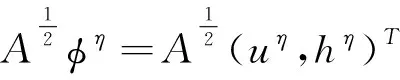
由引理2.2及定理2.1推算得，

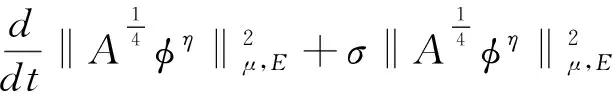
(17)

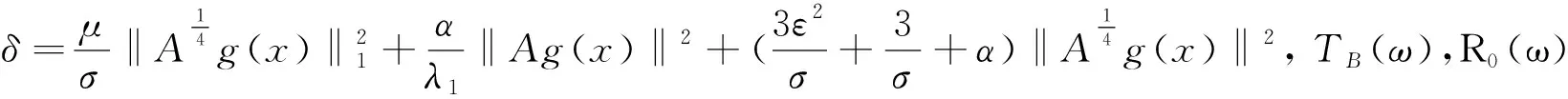
因此，取(10)中ϑ=σ，由(10),(17)及Gronwall不等式得，

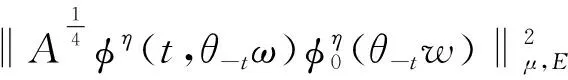
而‖z(θ-tω)‖2eσtr2(ω)，且r(ω)是缓增随机集。

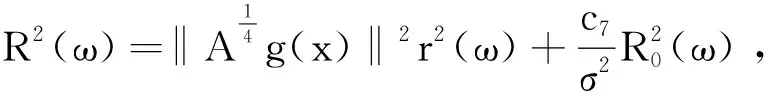
由于φ(t,θ-tω)φ0(θ-tω)=φ(t,θ-tω)(φ0-(0,gz(θ-tω))T)-(0,gz(ω))T，

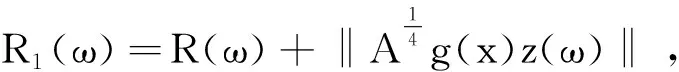
因此对所有的ω∈Ω，(14)成立。

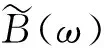
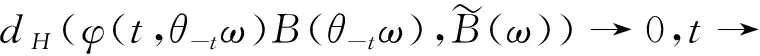
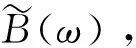
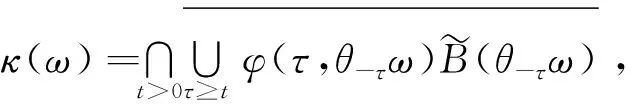
证明由引理2.3和(18)及定理2.1直接得到。