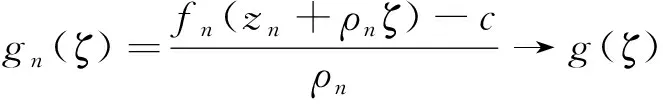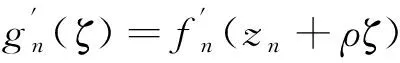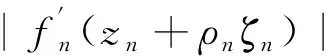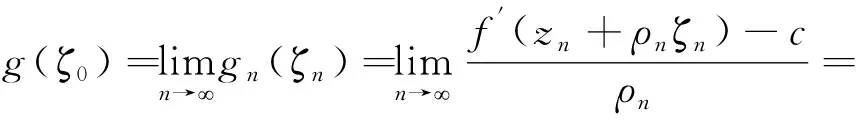分担集合的亚纯函数正规族
2018-10-10吕凤姣刘芝秀
吕凤姣, 刘芝秀
(1.黄河科技学院 信息工程学院,河南 郑州 450063;2.南昌工程学院 理学院,江西 南昌 330099)
1 引言及主要结果
设f(z)为开平面上非常数的亚纯函数,主要采用值分布论中的相关记号[1][2]。
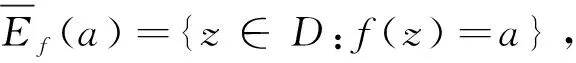
设f(z),g(z)为区域D上的两个亚纯函数,对复数a∈C,若f(z)-a的零点为zn(n=1,2,3,…),如果zn(n=1,2,3,…)也是g(z)-a的零点(不计重数),则称单向分担a,记为f(z)=a⟹g(z)=a。
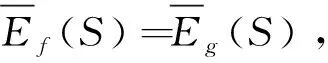
亚纯函数族F称为区域D上的正规族是指对F中的任意函数列{fn(z)}都存在子列{fnk(z)}在区域D上按球面距离内闭一致收敛。
亚纯函数族F在点z0正规,是指在存在点z0的邻域U(z0)使得F在U(z0)上正规。
F在区域D上正规等价于F在区域D上每一点都正规。
Montel首先将正规族与函数的取值联系起来,建立了著名的Montel正规定则。
定理A[3]设F={f(z)}是区域D内的一族亚纯函数,a1,a2,a3是扩充复平面£上三个互异的复数,如果对任意的f∈F,f(z)≠a1,a2,a3,则F在D内正规。
顾永兴在文[4]中进一步将正规族和函数导数的取值联系起来,建立了著名的Gu正规定则。
定理B[4]设F={f(z)}是区域D内的一族亚纯函数,k是正整数,a是非零有穷复数,如果对任意的f∈F,f(z)≠0,f(k)(z)≠a,则F在D内正规。
Schwick于1992年在文[5]中将函数与其导数唯一性条件即分担条件引入了正规族,建立了下面的定理C。
定理C[5]设F={f(z)}是区域D内的一族亚纯函数,a1,a2,a3是三个互异的有限复数,如果对任意的f∈F,f与f′同时分担值a1,a2,a3,则F在D内正规。
方明亮推广了Schwick的结果,证明了分担集合的情况。
定理D[6]设F={f(z)}是区域D内的一族全纯函数,S={a1,a2,a3},其中a1,a2,a3是三个互异的有限复数,如果对任意的f∈F,有f和f′分担集合S={a1,a2,a3},那么F在D内正规。
2007年,刘晓俊和庞学诚在文[7]中进一步将全纯函数族推广到了亚纯函数族。
定理E[7]设F={f(z)}是区域D内的一族亚纯函数,S={a1,a2,a3},其中a1,a2,a3是三个互异的有限复数,如果对任意的f∈F,有f和f′分担集合S={a1,a2,a3},那么F在D内正规。
自然地,我们要问定理E中的集合S中的元素个数是否可以减少,答案是否定的,有反例说明。
例设S={1,-1}和F={fn(z):n=2,3,4,…},其中
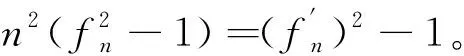
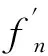
但是F在D内不正规。
如果从另外一种角度继续考虑分担集合的正规族问题,这里的f和f′分担集合S可否进一步减弱为单向分担呢?事实上,本文证明了下面的结果。
定理1设F={f(z)}是区域D内的一亚纯函数族,a,b,c是三个相互判别的有穷复数,S={a,b},A为有穷正数,如果对于任意的f(z)∈F,有f(z)-c的零点重级至少为1,且满足两个条件:
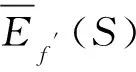
(ⅱ)当f(z)=c时,有|f′(z)|A且0<|f″(z)|A,
则F在区域D内正规。
下面举例说明定理1中的条件(ⅱ)是不能省略的。
例设D={z:|z|<1},S={a,b},c=0,其中|a|+|b|<1。
假设F={fn(z):n=1,2,3,4,…},且fn(z)=nz,D={z:|z|<1},

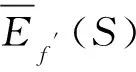
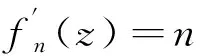
2 基本公式和引理
引理1[8-10](Zalcman-Pang引理)设F是单位圆盘Δ上的亚纯函数族,如果对∀f∈F和f(z)=0,存在一个正数A,使得|f′(z)|A。那么,如果F不正规,则对任意的0α1,存在
(ⅰ)实数0 (ⅱ)复数列zn,|zn| (ⅲ)函数列fn∈F; (ⅳ)正数列ρn→0+; 引理2[11]设f(z)是复平面上的有限级亚纯函数,k为正整数,f(z)的零点重级至少为k+2,f(k)(z)≠1,则f(z)为常数。 引理3[12][13]设f(z)是复平面上的有限级超越亚纯函数,k为正整数,其零点重级至少为k,A为正实数,若当f(z)=0时,|f(k)(z)|A,则对于任意l,1lk,f(l)(z)取任意有穷非零值无穷多次。 其中g(ζ)为复平面£上的非常数亚纯函数,且g#(ζ)g#(0)=h+1, g(ζ)的零点重级至少为1,g(ζ)的级至多为2。 可以断言: (ⅰ)g(ζ)=0⟹|g′(ζ)|h, (ⅱ)g′(ζ)≠a,g′(ζ)≠b。 事实上, (ⅰ)假设存在ζ0∈£使得g(ζ0)=0, 由于g(ζ)不恒等于0,根据Hurwitz定理得,存在ζn,ζn→ζ0,使得 则 fn(zn+ρnζn)=c。 由已知条件可知, 于是可得:g(ζ)=0⟹|g′(ζ)|h故(ⅰ)得证。 下面再证(ⅱ)。假设存在ζ0∈C使得g′(ζ0)=a。 显然g′(ζ)不恒等于a, 若g′(ζ)≡a=0,则g(ζ)为一常数函数,这与g(ξ)的零点重级至少为1矛盾。 若g′(ζ)≡a≠0,则g(ζ)为一次多项式, 设ζ1为g(ζ)的唯一一个重级为1的零点,故g(ζ)=a(ζ-ζ1)。 通过计算可得: g#(0) 则g#(0)<(|a|+1)+1与g#(0)=h+1矛盾(当h>max {|a|+|b|}+1时)。 于是可得g′(ζ)不恒等于a成立。 由于g′(ζ0)=a,但g′(ζ)不恒等于a,由Hurwitz定理可得: 存在gn(ζ)和点列ζn→ζ0,使得当n充分大时,有 fn(zn+ρnζn)∈S。 则 fn(zn+ρnζn)=a或者fn(zn+ρnζn)=b。 从而 这与g′(ζ0)=a矛盾,因此g′(ζ)≠a成立。 同理可得,g′(ζ)≠b,于是(ⅱ)得证。 假设g为超越亚纯函数,因为a,b是两个相互判别的复数,所以a,b中至少有一个不为零。不妨设a为非零常数,由于g的级至多为2,且满足(ⅰ)g(ζ)=0⟹|g′(ζ)|h,(ⅱ)g′(ζ)≠a,g′(ζ)≠b, 由引理3可得,g′(ζ)-a有无穷多个零点,与g′(ζ)≠a矛盾,因此假设不成立。 所以g为有理函数,因为有理函数至多只有一个Picard例外值,这与g′(ζ)≠a,g′(ζ)≠b矛盾。 综上所述定理得证。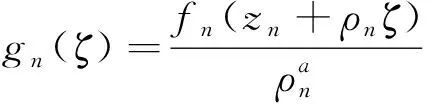
3 定理证明