一类带有区间时变时滞的非线性中立切换系统的指数镇定
2018-10-10王永昭
王永昭
(1.安阳师范学院 数学与统计学院,河南 安阳 455000;2.天津大学 管理与经济学部,天津 300072)
切换系统为动态混杂系统中的一种,大量出现在实际模型中,如无人机路径控制、供电系统、人工智能和机器人语言切换系统等。由于近些年来在工业应用上的增加,引起了国内外科研工作者的广泛关注[1-4]。能控性、稳定性是系统正常运转的重要指标,目前关于切换系统的研究,主要集中在稳定性和能控性方面,随着研究的不断深入,他们已经取得了一些有价值的成果[5-7]。由于切换系统本身较复杂,不可避免的受一些因素影响,例如时滞、随机扰动、非线性项以及中立项等。然而,在众多研究文献中对于带有区间时滞的中立切换系统的镇定及反馈控制器设计的研究较少,所以对该类切换系统的研究很有价值。
本文针对区间时滞切换系统研究其稳定性。首先给出时滞以及时滞的上下界,构造Lyapunov-Krasovskii函数,利用平均驻留时间方法找到切换规律,得到了带有区间时变时滞中立非线性切换系统指数镇定的充分条件,最后运用Schur补引理,反馈控制器进一步被设计出,通过数值例进行仿真。
1 问题描述
考虑带有区间时滞的非线性中立切换系统
(1)
其中u(t)∈Rm为控制输入,x(t)∈Rn为状态,φ(s)∈Rn为初始条件,A,B1i,B2i,Ci(i∈L)为常矩阵,切换信号σ(t):[0,]→L={1,2…,n}为分段连续函数,n为子系统数,t0是切换初始时刻,tk为第k次切换时刻,{(t0,σ(t0)),(t1,σ(t1)),…,(tk,σ(tk)),…}为切换序列,时滞函数τ(t)满足
τmτ(t)d<1。
(2)
非线性扰动函数为f(t,x(t-τ(t)))且满足
‖f(t,x(t-τ(t)))‖ε‖(x(t-τ(t)))‖,
式中ε为大于0的常数。
对于系统(1),我们考虑形式为
u(t)=Kσ(t)x(t)
(3)
的反馈控制函数,其中Ki,i∈L为反馈增益矩阵。
(4)
定义1[7]对任意的t2>t1≥0,记Nσ(t1,t2)为切换信号σ(t)在区间(t1,t2)上的切换次数,给定N0≥0,τa≥0,如果
Nσ(t1,t2)N0+(t2-t1)/τa
(5)
那么τa称为平均驻留时间,一般取N0=0。
定义2[8]如果闭环系统(4)的解满足
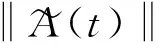
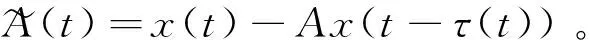
引理1(Schur补引理)[9]给定对称矩阵S1,S2,S3且
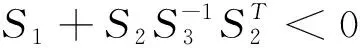
当且仅当
引理2[10]令D,S和W为适当维数的实矩阵且W>0,那么对任意适当维数的非零向量x,y,有下式成立
2xTDSyxTDWDTx+yTSTW-1Sy。
假设1假设ρ(A)<1,ρ(A)为矩阵A的谱半径。
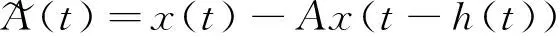
2 主要结果
定理1对给定的正常数α和β≥1,若存在正标量ε和对称正定矩阵Pi,Qi,Ri,使得以下矩阵不等式对任意的i,j∈L,i≠j成立:
PiβPj,QiβQj,RiβRj∀i,j∈L,
(6)
(7)
其中
证明:考虑Lyapunov-Krasovskii函数
(8)
其中
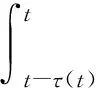
沿着系统的轨线求导,可以得到
因此,我们可得
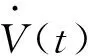
-(1-d)e-ατMxT(t-τ(t))Qix(t-τ(t))-2[Ax(t-τ(t))]TPiEi(T)
由于‖f(x(t-τ(t),t))‖ε‖(x(t-τ(t)))‖,则我们可以得到
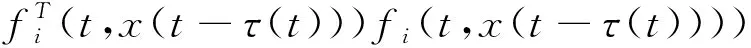
利用引理2可得
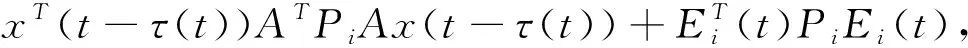
-2[Ax(t-τ(t))]TPif(t,x(t-τ(t)))≤xT(t-τ(t))ATPiAx(t-τ(t))+fT(t,x(t-τ(t)))Pif(t,x(t-τ(t)))。
联立以上三式式可得
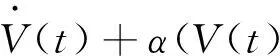
-fT(t,x(t-τ(t)))(Pi-I)f(t,x(t-τ(t)))。
令ζ(t)=[xT(t)xT(t-τ(t))fT(t,x(t-τ(t)))]T。
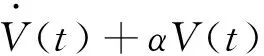
其中ψi由(7)式给出。因此有

当t∈[tk,tk+1)时,上式两边取从tk到t的积分,我们可得
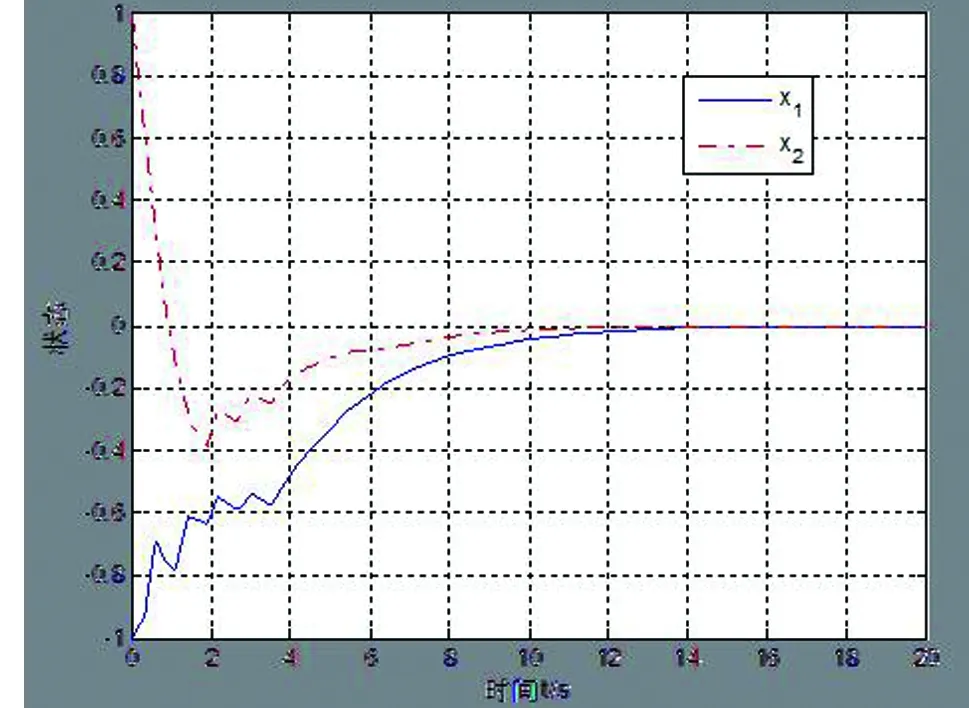
V(t)=Vσ(t)(t)e-α(t-tk)Vσ(tk)(tk),tkt 由上式和k=Nσ(t,t0)(t-t0)/τa,我们得到下面的结果 因此,可得 其中 联立以上两式式可得 由定义2可得,闭环系统(4)为指数镇定的。 定理2对于给定的正常数α和β≥1,如果存在正常数ε,对称正定矩阵Xi,Gi,Oi,和矩阵Yi满足下面的矩阵不等式: XjμXi,GjμGi,OjμOi, ∀i,j∈L,i≠j, (9) 其中 解出。 证明:由于Gi>0,Oi>0,可以得到 (Gi-Xi)TG-1i(Gi-Xi)≥0, 有 (10) 其中 考虑系统(1)的两个子系统,参数如下: 取α=1.35,β=1.6,d=0.3,τM=0.5,ε=0.4。 那么可得 利用定理2可得 图1 系统状态轨线Fig.1 State response of the system 控制器收益为: 假设系统的初态为x(0)=(-1 1)T,利用Matlab仿真可得闭环系统的状态轨线图,见图1。 本文主要研究了区间时变时滞的非线性切换系统的指数稳定性。利用时滞以及时滞的界建立Lyapunov-Krasovskii函数,得到使切换系统镇定的充分条件,运用Schur补引理,进而设计出该系统的控制器,最后给出数值例,检验所获得结果的有效性。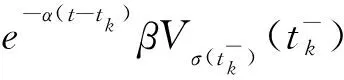
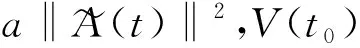
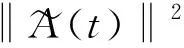
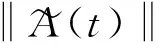
3 数值仿真
4 结 论
