底吹钢包气-钢-渣三相流过程离散-连续转化及联合算法

李林敏， 李宝宽， 许 昌， 胡代清， 刘玉成

(1. 河海大学 能源与电气学院, 南京 211100; 2. 东北大学 冶金学院, 沈阳 110819;3. 安徽金寨抽水蓄能有限公司, 安徽 六安 237300)

钢包底吹氩搅拌可以使钢包内钢液的温度和成分均匀化并去除夹杂物，具有高效率、低成本和易操作等优势[1, 2].喷吹参数对搅拌过程将产生重大影响；强搅拌可以减小钢液均混时间，但可能造成钢液裸露形成二次氧化、发生卷渣或侵蚀包壁等；小流量的稳定喷吹则可以促使夹杂物上浮，但增加了混均时间可能导致温度不均匀.该过程由气-钢-渣三相组成，既包含分离界面又存在相对离散且大小不一的气泡，流动情况复杂且在高温状态下，很难进行工业实验及测量.因此，建立一个完善的数学模型来描述其复杂的流动现象及相间相互作用机理具有重要意义.

针对底吹钢包中的气-钢-渣三相流过程，现有方法主要有欧拉方法[3-6]和欧拉-拉格朗日混合方法[7-9].在欧拉方法中，Li等[10]和Llanos等[11]采用VOF(Volume of Fluids)界面追踪算法较好地描述了渣层界面的行为.Li等[12]采用多流体算法耦合人口平衡模型(Population Balance Model, PBM)研究了气泡粒径分布规律以及渣眼面积和混匀时间随不同参数的变化规律.此外，人口平衡模型和多流体算法还被成功应用于预测钢液中夹杂物的输运、碰撞聚合及去除行为等[13].针对气泡在液体中呈弥散分布，而渣层与钢液则表现出较明显的分层特性，Liu等[14]和Cloete等[15]结合基于拉格朗日方法的离散相模型(Discrete Phase Model, DPM)和VOF界面追踪方法分别求解了离散气泡运动以及渣层波动行为，并在不同工艺中得到了应用[16-18].为了更好地描述气泡、钢液和渣层之间的相互作用及其非稳态流动规律，本文作者等[19-21]考虑气泡合并以及离散气泡在上表面与空气层的融合，建立了离散气泡模型(Discrete Bubble Model, DBM)，并结合VOF界面追踪方法和大涡模拟方法(Large Eddy Simulation, LES)[22]求解了钢包底搅过程，较好地描述了离散气泡运动、渣层波动、渣滴形成、渣眼形态及其演变规律等，得到了准确的渣层形态特征，较好地描述了气泡和液体的相互作用.但上述离散气泡模型仅考虑了气泡的粒径变化，无法描述气泡的变形，造成了计算误差.特别是当气体流量较大时，将产生更多较大尺寸的气泡，造成更大的误差.

考虑上述模型缺陷，本文研究的目标是：在上述离散气泡和连续界面联合算法的框架下，针对气泡建立一种离散-连续转化模型，在对小尺度离散气泡进行模型化求解的同时，直接追踪较大尺度可分辨的气泡边界以对其进行完整描述，并建立大小尺度气泡间的转化模型以实现两者的分级耦合求解；对于更大尺度的自由界面，同样采用界面追踪法模拟；由此，当求解尺度确定的时候，既完整地描述了可分辨的流体边界运动行为，又考虑了小尺度离散气泡的影响；为揭示底吹钢包内气-钢-渣三相流流动规律以及理解相间相互作用机制提供更有力的理论保障.

1 模型描述

多相流数值算法中，多流体方法只能得到各相的宏观分布特征；界面追踪法虽然可以完整地描述相界面结构，但其精度会受到求解尺度的限制；离散相模型可以描述每个离散粒子的运动行为，但难以描述连续流体的运动.针对宏观的钢包底搅过程，分辨所有气泡边界所需计算量巨大，而渣层的自由界面又适合采用界面追踪算法.因此，本模型的思路是采用VOF界面追踪方法直接描述计算域特定求解尺度下的可分辨界面，对小尺度不可分辨的气泡采用DBM离散气泡模型进行跟踪模拟.针对气泡建立DBM-VOF转化与联合算法，来对不同尺度的气泡进行完善地求解.对于湍流，采用LES大涡模拟方法，即同样对可求解尺度大涡进行直接求解，而对小尺度涡进行模型化计算.本模型的思路如图1所示.

图1 本文算法框架示意图Fig.1 Sketch of modeling framework

1.1 VOF界面追踪法

VOF方法通过求解其中一相的体积分数即相分率的连续性方程来追踪流体的边界，对于第k相，其相分率的连续性方程如下：

(1)

式中：α代表相分率，u代表速度.

钢包底搅过程共包含气、液、渣三种连续相，本文求解的是气体和渣的相含率αgas和αslag，液相含率αl则可由下式求解：

αl=1-αgas-αslag

(2)

VOF方法针对所有流体求解一套动量方程，流体属性(密度ρ和黏度μ)则通过以下方程求解：

ρ=αlρl+αgasρgas+αslagρslag

(3)

μ=αlμl+αgasμgas+αslagμslag

(4)

1.2 大涡模拟

多相流动过程往往是不稳定、时刻变化的.为更好地描述该过程的非稳态特性，本文采用大涡模拟方法，直接描述大尺度涡流，而对小尺度涡进行模型化描述.该方法通过滤波函数对Navier-Stokes方程进行处理，滤波后的方程如下：

(5)

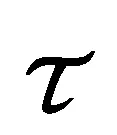
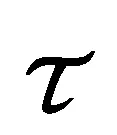
(6)

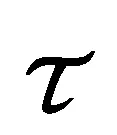
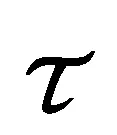
(7)

(8)

式中：δij当且仅当i=j时，其值为1，否则为0.μt代表亚格子湍流黏度，通过下式求解：

(9)

式中：κ为von Kármán常数，本文取值为0.4，d为与邻近壁面的距离，V代表网格体积，Cs为Smagorinsky常数，取值0.1.

表面张力Fs则采用连续表面力模型进行求解：

(10)

式中：σ为表面张力系数，γ曲率的表达式为：

γ=-·(α/|α|)

(11)

离散气泡对连续流体的作用力之和Fb将在下一节中给出.

1.3 离散气泡模型

为求解流场中不可分辨气泡的运动行为及其与流场的相互作用规律，本文采用离散气泡模型在拉格朗日坐标系下对小气泡进行跟踪求解.每个气泡的运动方程如下：

(12)

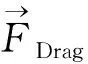
(13)

其中：db为气泡直径，Re为相对雷诺数，其定义为：

(14)

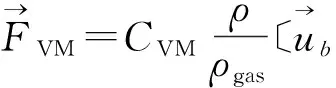
(15)

(16)

式中：CVM为虚拟质量力系数，取值为0.5.而离散气泡与连续流体相互作用的合力Fb则为曳力、虚拟质量力及压力梯度力之和.计算过程中通过对流体单元内所有粒子对流体作用力的积分求得流体的动量变化，从而实现了离散气泡与连续流体的双向耦合.

1.4 离散-连续转化模型

本文离散气泡的合并模型同作者等的前期工作[21]一致，而本文工作的关键在于考虑气泡合并所引起的粒径变化的基础上，引入离散-连续转化模型，以实现针对气泡的多尺度离散-连续联合求解算法.

为实现离散小气泡与连续大气泡的转化，本模型需对方程(1)中的气体相分率方程进行修改并添加由于离散气泡向连续气体转化所引起的源项:

(17)

本文的转化模型包含以下两种类型：(a)当小气泡合并成可分辨的大气泡时，在所处单元格添加与大气泡相同质量的源项，同时删除并停止跟踪合并后的离散气泡.(b)当小气泡遇到气-液界面且速度指向气相时，认为小气泡与大气泡发生融合，小气泡被大气泡吞并，移除离散小气泡并在所处单元添加小气泡同等质量的源项.上述两种转化形式的示意图如图2所示：

当上述两种转化方式发生时，式(17)中的源项Sb可写成：

Sb=Vb/(Vcell·Δt)

(18)

图2 离散-连续转化模型示意图Fig.2 Sketch of discrete-continuum transition model(a)—离散气泡合并为可分辨边界气泡；(b)—离散气泡与连续气体融合

上式只在转化发生时执行一次，其中： Δt为时间步长.此外，对所处网格的流体速度需按下式处理以考虑气泡的动量：

(19)

此外，当转化发生时，原离散气泡均被移除，不再追踪.

2 数值细节

为方便模型验证，本文针对一个1/3的底吹钢包水模型实验进行仿真计算.实验中采用水模拟钢液、食用油模拟渣液以及氮气模拟氩气.模型尺寸以及材料的物理属性如表1所示.

表1 几何参数及物料属性

续表

图3 计算域网格Fig.3 Mesh for simulation

计算域采用六面体网格划分，喷嘴处网格尺寸为4 mm，高度方向最大网格高度设置为8 mm，渣层处网格高度设置为4 mm.由于气泡基本位于喷嘴上方，该区域最大网格体积约为128 mm3，该体积对应的气泡直径为6.25 mm.因此，所建立的网格对气泡的分辨能力在6 mm以上.采用非稳态格式计算，时间步长取1×10-4s.压力-速度耦合采用PISO算法.计算域网格如图3所示.

计算中上表面设置为压力出口，入口边界条件为离散气泡的质量入口.实验观测得到入口处气泡平均直径约为1 mm，因此本文假设入口初始气泡直径为1 mm，气泡喷入量则根据气体流量Q和初始气泡直径dbi换算：

(20)

式中：Nin代表喷嘴处气泡注入的速率.

3 结果分析与讨论

3.1 离散气泡行为

本模型假设出口处产生的均为粒径较小的离散气泡，计算中以离散粒子的形式将气泡注入流场，初始直径为1 mm.注入后的气泡采用离散气泡模型进行模拟.由于模型中考虑了气泡的合并现象，计算中两个气泡可能发生合并形成一个较大气泡，导致气泡粒径的不均匀分布，且合并大多发生在0.2 m高度以内[21].本文选取了90, 110, 130和150 L/h四种气体流量进行计算，渣层厚度均为40 mm.其中，气体流量在90 L/h时，喷嘴上方的气泡分布及其合并过程的计算结果如图4所示.

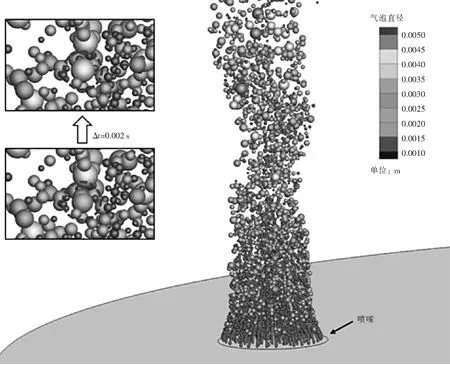
图4 离散气泡分布及合并行为Fig.4 Distribution and aggregation of discrete bubbles

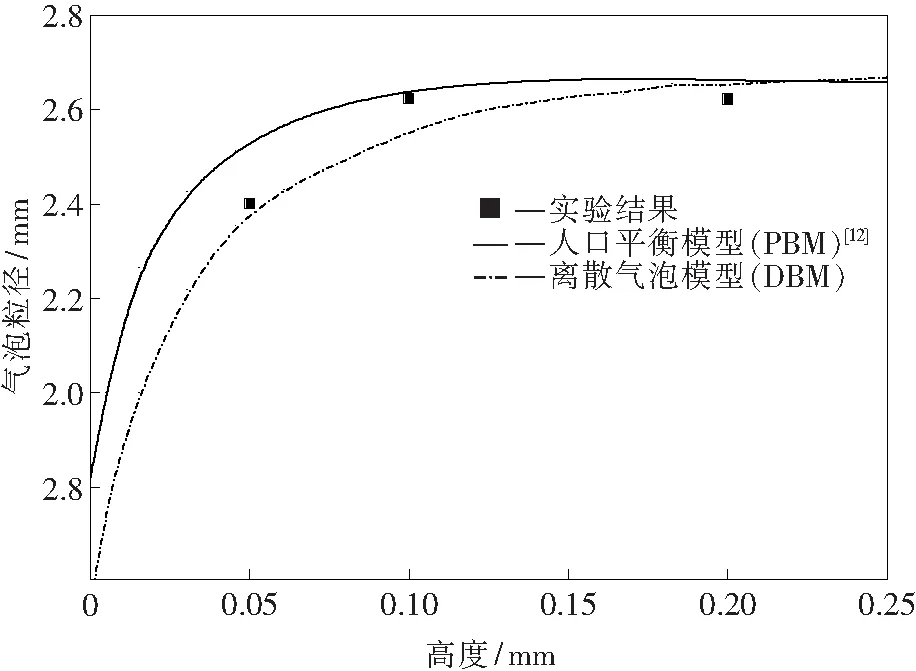
图5 离散气泡模型得到的气泡直径变化与实验及人口平衡模型结果对比Fig.5 Bubble diameter calculated by DBM, experimental data and that from PBM

可以发现，本模型很好地描述了离散气泡的分布特性，由于离散气泡模型所考虑的气泡直径较小，这些气泡在上升过程中极少发生破碎，因此本文模型中只考虑了离散气泡的合并.图4左上方显示了计算得到的气泡合并过程.离散气泡算法得到的高度方向上的时均粒径分布与实验结果和人口平衡模型结果对比如图5所示.

从结果中可以看出，人口平衡模型预测的气泡粒径增长速率大于实验结果和离散气泡模型计算结果，离散气泡模型得到的粒径分布则更接近于实验结果；说明本文离散气泡模型可以较准确地描述钢包底搅过程中小气泡的运动行为，并准确预测气泡粒径分布.

3.2 离散气泡与连续气体的转化及耦合

随着气泡向上运动以及气泡间合并的发生，将产生越来越多的大尺度气泡；当这些大气泡足以被计算域网格所分辨的时候，本文算法将其转化为连续气体，并通过界面追踪方法来完整地描述其运动、变形以及合并破碎等；从而解决了离散气泡模型难以准确描述较大尺度气泡的问题.图6展示了本模型计算得到的不同流量下离散气泡的分布和连续气体的边界形态特征.

从图中可以看出，气体流量较大的情况下产生了更多较大尺度的连续气泡，且上表面波动也更为明显.由于该网格尺度可分辨的气泡直径约为6 mm，因此，我们也可以看到采用离散气泡模型跟踪的离散气泡直径均为6 mm以下.较大尺度的可分辨边界气泡则由气液相界面表示.结果表明：该方法实现了针对不同尺度气泡的联合求解，既完整地描述了较大尺度气泡，又可以考虑不可分辨的小尺度气泡的影响，可以在有限的计算资源内对复杂的相分布进行尽可能完善地求解.如需分辨更小尺度的气泡边界，可通过减小空间离散尺度实现.同时，所需求解的离散气泡尺度也将减小，计算量将增加.计算过程中发生的离散气泡与连续气体的转化过程如图7所示.

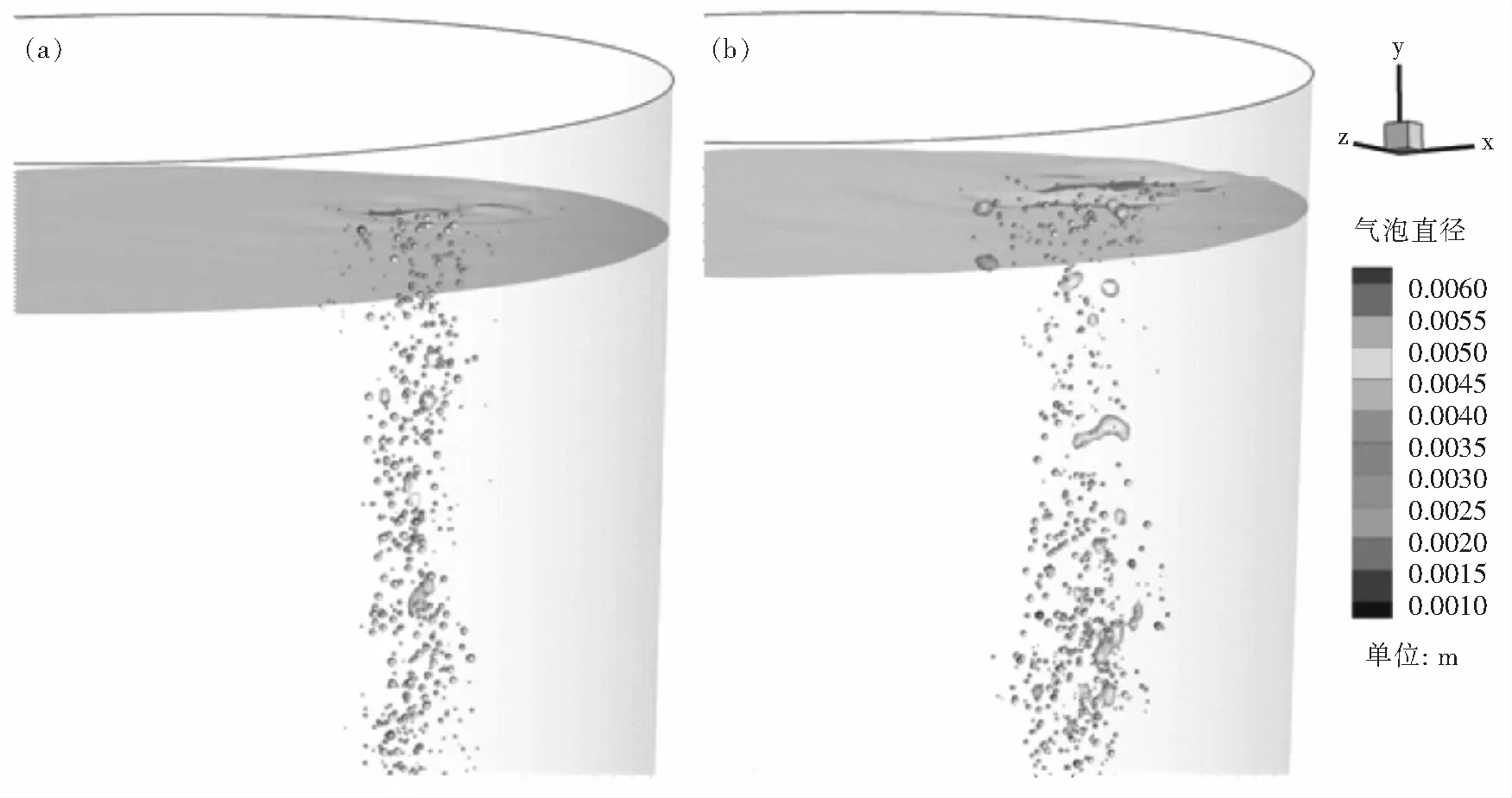
图6 不同流量下的气泡分布Fig.6 Simulation results of bubble distribution with different gas flow rates(a)—Q=90 L/h； (b)—Q=150 L/h

图7 两种类型转化过程的计算结果Fig.7 Simulation results for the transitions(a)—离散气泡合并及离散-连续转化过程Δt=0.004 s；(b)—离散气泡合并以及离散气泡与连续气体的合并过程Δt=0.004 s

图8 连续大气泡的合并及破碎过程Fig.8 Simulation results of aggregation and breakage of large bubbles(a)—合并； (b)—破碎

图9 不同气体流量下的渣层形态Fig.9 Results of slag layer features with different gas flow rates(a)—Q=90 L/h； (b)—Q=150 L/h

图7(a)所示的过程为两个离散气泡在上升过程中合并为一个较大气泡，而所产生的较大气泡是可分辨的，因此在合并的同时，大气泡直接被移除并转换为采用界面追踪法求解，形成了一个较大气泡的连续体，并采用气液相界面描述.图7(b)首先展示了两个小气泡的合并过程，合并后的气泡仍为较小的离散气泡并被继续跟踪.而后，当其运动到连续气泡边界时，该离散气泡与连续气泡发生合并，离散气泡不再被跟踪.连续气泡则由于接收了小气泡的质量，其尺寸进一步增大.对于连续的大气泡，其合并及破碎行为则可以直接被界面追踪法求解，过程如图8所示.

由于较大尺度的气泡边界被直接求解，其变形以及合并破碎过程均可以被完整地描述.结果表明，模型可以在对可分辨尺度气泡进行完全求解的同时，进行小尺度气泡的模型化求解，离散气泡尺度不受网格限制，实现了针对气泡的多尺度耦合求解.

3.3 渣层行为

对于渣层，由于其表现出较明显的分层特性，且界面相对连续，界面的形态对渣金反应的影响显著.本文采用VOF界面追踪方法对其边界进行直接求解，以对渣层的界面行为进行准确描述.计算得到的气泡分布和渣层在不同流量下的形态如图9所示.

从图中可以看出，本模型非常真实地还原了渣层界面的形态特征.在气泡的搅拌下，渣金界面产生了剧烈的变形，且气体流量越大，界面变形越明显，也越容易发生卷渣.可以看到，在气体流量达到150 L/h时，渣层下表面产生了较多渣滴.为研究渣眼和渣滴的形成机理，做出渣眼附近的速度场结果如图10所示.

图10 渣眼处速度分布Fig. 10 Flow field near the slag eye

由于本文采用了大涡模拟方法，它可以直接对大尺度的涡进行求解，对宏观尺度的流动规律可以进行较好地描述.可以看到，渣眼中心处液体在气泡的作用下向上表面运动，并将渣液排开.当气泡从上表面溢出后，液体在重力作用下又转向下运动，向下运动的液体与上涌的气泡及液体相遇时，便形成了涡旋.这种涡旋是造成渣金界面的变形、波动及卷渣等的主要原因.当涡旋的强度较大时，便会造成部分渣液脱离形成渣滴，并夹带渣滴向下运动.可见，该方法很好地揭示了渣金界面结构演化规律及渣滴形成机理.针对渣眼形态，不同气体流量下的计算结果与实验结果对比如图11所示，计算和实验中渣层的厚度均为40 mm.

从渣眼形态的定性对比可以看出，本模型在宏观上得到了与实验结果较吻合的渣眼形态和大小.

4 结 论

本文建立了离散气泡模型(DBM)和界面追踪方法(VOF)的转化及联合算法，针对底吹钢包气-钢-渣三相流过程进行了多尺度的仿真计算.特别是针对其中不均匀分布的大小气泡，实现了同时对可分辨尺度气泡的直接求解和小尺度不可分辨离散气泡的模型化计算.模型可在一定的计算域求解尺度内，尽可能完整地求解相结构分布，实现了不同尺度相结构的分级耦合求解.为完善地描述底吹钢包内的复杂多相流现象、揭示相间的相互作用机理和各相流动规律提供一种切实可靠的算法.本文结论总结如下:

(1)离散气泡模型较好地模拟了小尺度气泡运动和合并行为，气泡合并大多发生在0.2m高度以内，得到的粒径变化相比人口平衡模型与实验结果更为吻合.

(2)所建立的离散-连续转化算法实现了离散气泡与长大后的可分辨气泡的转化，以及离散气泡与连续气泡的聚并，实现了不同算法框架之间的耦合，解决了离散气泡模型无法考虑气泡变形的问题，本文所建立的网格可直接求解直径为6 mm以上的气泡.

(3)模型得到了真实的渣层形态，完善地描述了大气泡合并破碎行为、渣滴及渣眼的形成与演化规律，得到了与实验结果较吻合的渣眼形态和大小.

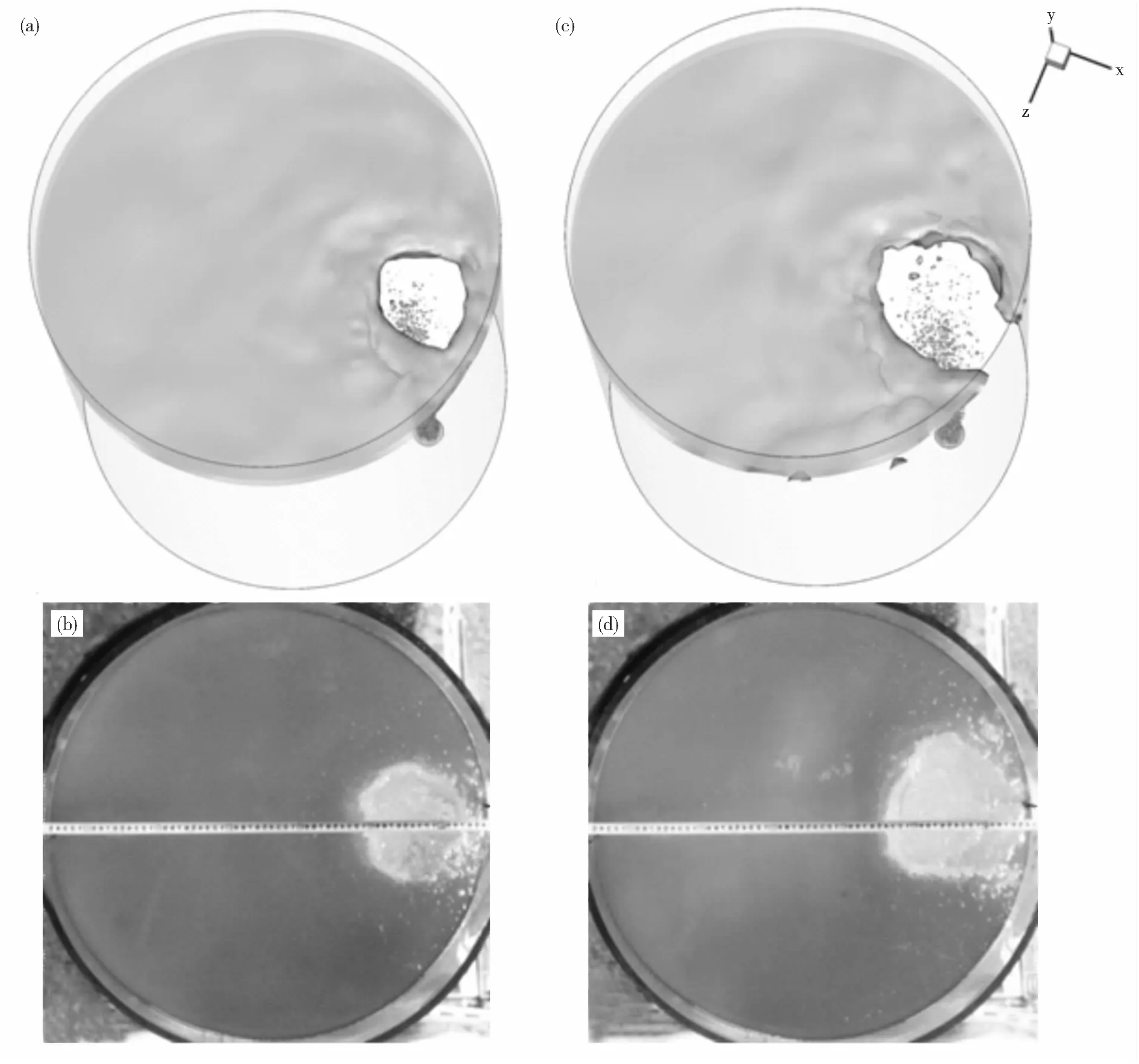
图11 渣眼形态计算结果与实验结果对比Fig.11 Slag eye features, simulation and experiment results(a)—90 L/h计算结果； (b)—90 L/h实验结果； (c)—150 L/h计算结果； (d)—150 L/h实验结果