用多个光子晶体实现量子纠缠态的稳定性
2018-10-09刘晓静刘继平张晓茹张斯淇陆景彬吴向尧
刘晓静, 刘继平, 张晓茹, 刘 晗, 潘 庆,梁 禺, 张斯淇, 陆景彬, 吴向尧
( 1. 吉林师范大学 物理学院, 吉林 四平 136000; 2. 吉林大学 物理学院, 长春 130012)
量子信息学由量子力学和信息科学组成, 目前在理论和实验方面已取得较多研究成果[1-2], 其中量子纠缠态在量子通信、 量子隐形传态、 量子计算和量子密码技术等领域应用广泛[3-11]. 但由于各种环境噪声, 量子纠缠度会随着传输距离的增加而变小, 甚至趋于零[12], 即出现退相干现象, 因此如何保持量子纠缠态的纯度已成为量子信息中需要解决的关键问题.
光子晶体的折射率可发生周期性变化[13-14], 光波在其中传播时, 某些频率的光波受到抑制, 从而形成光子禁带或带隙[15], 类似于半导体材料中电子的能带结构. 光子晶体中的缺陷在带隙中产生缺陷态, 从而形成光子的局域化[16], 这些特性使光子晶体可制作微腔、 光子晶体激光器、 光学滤波器、 光子二极管、 光开关和光波导等光学器件[17-18].
本文用多个光子晶体实现量子纠缠态的稳定性. 计算结果表明: 对两光子和三光子纠缠态, 当叠加参数c1=0.52~0.86时, 纠缠度E=0.8~1;c1在其他区域时,E较低或趋于零. 因此纠缠减弱或不再纠缠. 本文设计一组一维光子晶体, 当两光子或三光子的纠缠光通过该组光子晶体, 且叠加参数c1=0.03~0.98时, 纠缠度E=0.8~1, 从而使量子纠缠态可远距离传输, 更好地实现量子通信.
1 一维光子晶体的传输矩阵和透射率
对于一维光子晶体, 由传输矩阵法可知第i层介质的传输矩阵[17]为
(1)
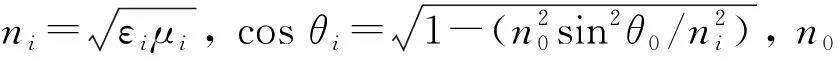
(2)
透射率为
(3)
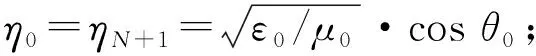
2 两光子和三光子的极化纠缠态和量子纠缠度
两光子的极化纠缠态为
(4)
三光子的极化纠缠态为
(5)
其中|H〉和|V〉表示单光子电场E水平偏振和垂直偏振.
由于各种环境噪声, 量子纠缠态的纠缠度随传输距离的增加而变小. 式(4)和式(5)分别为两光子和三光子的最大纠缠态, 传输过程中分别变为

(8)
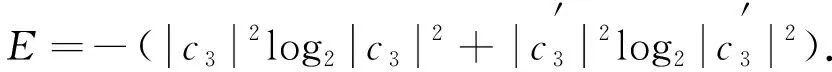
(9)
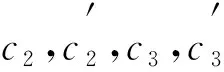
由式(3)可得在一维光子晶体中输出和输入电场强度间的关系为
Eout=tEin,
(10)
其中:t为透射系数;Eout和Ein分别为输出和输入电场强度. 在式(6),(7)中, 当两光子或三光子入射一维光子晶体时, 输出的水平偏振态|H〉和垂直偏振态|V〉的电场分别为
(11)
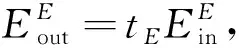
(12)
其中:tM和tE分别为|H〉和|V〉的透射系数;Ein为入射光的电场;Eout为经过一维光子晶体后的输出光电场. 输入纠缠态
通过一维光子晶体后, 其输出纠缠态变为
如图1所示, 其中PC表示一维光子晶体.

图1 |ψ〉in和|GHZ〉in通过光子晶体PC变为|ψ〉out和|GHZ〉outFig.1 |ψ〉in and |GHZ〉in change into |ψ〉out and |GHZ〉out through photonic crystal PC
式(15),(16)的归一化形式为
同理,n光子的输出纠缠态为
(19)
其中归一化系数分别为
以两光子和三光子为例, 计算其输出纠缠态的量子纠缠度, 分别为
其中:
(22)
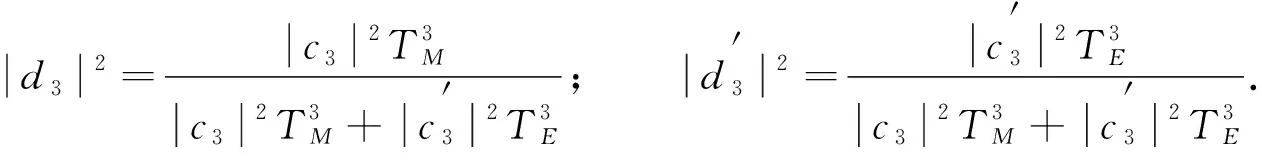
(23)
由式(22),(23)可见, 在通过光子晶体后, 输出量子纠缠态的纠缠度与一维光子晶体透射率TM和TE有关, 由于透射率0≤TM≤1, 0≤TE≤1, 因此选择合适的TM和TE值, 两光子和三光子纠缠态的纠缠度可被放大.
3 结果与讨论
下面给出两光子和三光子纠缠度的数值结果. 先计算TM和TE波的透射率. 主要参数为: 中心波长ω0=1.22×1015Hz, 介质A的折射率nA=1.68, 厚度a=108 nm, 介质B的折射率nB=2.56, 厚度b=198 nm, 结构为(AB)16, 入射角θ0=π/6, 由式(1)~(3)计算TM波和TE波的透射率, 结果如图2所示. 由图2可见, TM和TE波的透射率分别为0≤TM≤1和0≤TE≤1. 由式(8)可计算两光子输入纠缠态的量子纠缠度, 由式(20),(22)可计算两光子输出纠缠态的量子纠缠度, 结果如图3所示.

图2 一维光子晶体TM波(A)和TE波(B)的透射率TFig.2 Transmittance T of TM (A) and TE (B) wave in one-dimensional photonic crystals
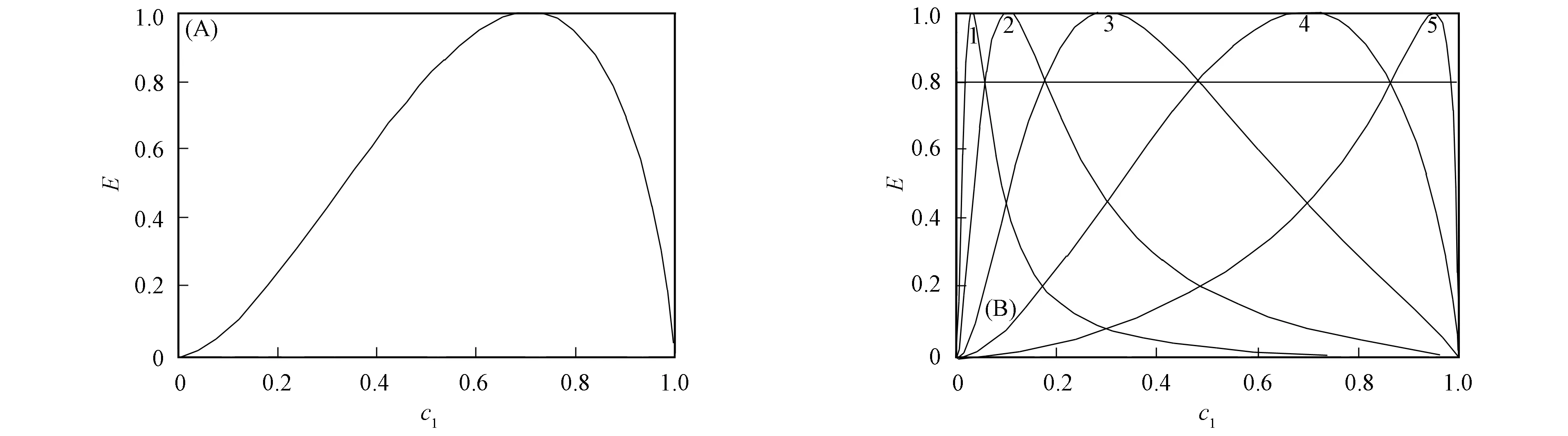
图3 两光子输入(A)和输出(B)纠缠态的纠缠度曲线Fig.3 Entangled degree curves for two photons input (A) and output (B) entangled states
由图3(A)可见, 当0.52≤c1≤0.86时, 0.8≤E≤1, 在其他区域,E降低或趋于零. 即受到外界干扰时, 量子纠缠态不能远距离传播. 由图3(B)可见, 它由5个输出量子纠缠度曲线构成. 曲线1~5对应的透射率分别为(TE=0.032,TM=0.99), (TE=0.1,TM=0.978), (TE=0.25,TM=0.8), (TE=0.77,TM=0.8)和(TE=0.8,TM=0.265). 5组不同的透射率可通过5个不同结构的一维光子晶体实现. 当0.03≤c1≤0.98时, 两光子输出纠缠度0.8≤E≤1. 可见, 当0.8≤E≤1时, 两光子输出远大于输入纠缠度c1的取值范围, 从而实现两光子纠缠态远距离传播. 由式(21),(23)可计算三光子输出纠缠态的纠缠度, 结果如图4所示, 它由5个输出量子纠缠度曲线构成, 曲线1~5对应的透射率分别为(TE=0.1,TM=0.58), (TE=0.195,TM=0.53), (TE=0.35,TM=0.45), (TE=0.9,TM=0.55)和(TE=0.8,TM=0.52). 由图4(B)可见, 当0.02≤c1≤0.97时, 三光子输出纠缠度0.8≤E≤1, 可进行远距离传播.

图4 三光子输入(A)和输出(B)纠缠态的纠缠度曲线Fig.4 Entangled degree curves for three photons input (A) and output (B) entangled states
综上所述, 当两光子或三光子纠缠态通过一组光子晶体传播时, 若其纠缠度0.8≤E≤1, 则其纠缠态可远距离传输, 使得量子通信可更好地实现. 计算结果表明, 对两光子和三光子纠缠态, 当叠加系数0.52≤c1≤0.86时, 纠缠度0.8≤E≤1, 当c1在其他区域时, 纠缠度E较低或趋于零, 即纠缠减弱或不再纠缠, 在光与环境相互作用即退相干效应下, 易使纠缠度降低或不再纠缠. 本文设计了一组一维光子晶体, 当纠缠光通过光子晶体, 且参数0.03≤c1≤0.98时, 纠缠度0.8≤E≤1, 使得量子纠缠态可远距离传输, 从而更好地实现量子通信.
