多传感器数据的处理及融合

陈 英, 胡艳霞, 刘元宁, 朱晓冬

(1. 南昌航空大学 软件学院, 南昌 330063； 2. 吉林大学 计算机科学与技术学院, 长春 130012)

多传感器系统的发展促进了数据融合技术的改进, 数据融合主要是对多源的数据进行融合, 其重点是数据的优化和综合操作. 目前已有许多相关研究, 如文献[1]基于Kalman滤波在数据关联的同时剔除野值； 文献[2]提出了一种基于奇偶抽取的剔除野值方法, 该方法对于连续型野值的剔除效果明显； 文献[3-4]提出了一种带监督情形下基于归一化残差的异常值检测方法, 该方法异常值门限大小的设置依赖于经验, 虽然选择较大的门限值可降低虚警率, 但其未给出具体的对应关系； 文献[5]提出了一种基于一阶差分和外推拟合的联合野值剔除方法, 首先对原始测量数据作一阶差分处理, 然后再对差分结果数据利用外推拟合法进行野值剔除； 文献[6]提出了利用残差和误差相关矩阵构造二次型判定野值的实时野值剔除方法； 文献[7]采用空间随机样本, 其独立于系统的模型, 可应用在各种系统模型下, 但其实现机理无法克服粒子退化和粒子多样性的溃退问题； 文献[8]提出了信息增量和目标权重相结合的方法实现多目标跟踪系统中传感器资源对目标的分配, 并给出了影响目标权重的距离和速度两个特征向量的量化方法； 文献[9]利用全信息融合模型模拟人类认知原理, 初步实现了对全信息数据的认知, 构建了全信息数据的多层、 多粒度解析与融合模型, 达到了随着信源信息量不断扩充与信息粒度不断加细, 融合结果的精度和信度逐步提升的目的； 文献[10]针对目前多传感器数据融合时各传感器的权值难确定的问题, 结合模糊理论, 提出了一种基于模糊熵的多传感器加权融合算法； 文献[11] 基于Kalman和模糊支持度对多传感器网络进行融合； 文献[12]利用粗糙集和方向传播神经网络对多传感器网络进行融合; 文献[13]针对权值固定的融合无法自适应的根据测量值优劣更有利的信息， 提出了一种将固定权值改进为动态权值的融合方法； 文献[14]利用粗大误差理论将明显偏离正常数据的异常数据剔除， 基于概率统计理论计算和更新节点信誉度， 只允许来源于高信誉度的节点数据参与数据融合； 文献[15]利用节点收集数据的时间和空间相关性， 提出了一种基于压缩感知理论的无线传感器网络数据融合算法.

上述工作多假设系统噪声和观测噪声为相关或独立的高斯噪声, 但在实际的多传感器应用中, 噪声多为非高斯系统, 所以上述方法并不适合非高斯观测噪声的情况. 基于此, 本文利用小波技术和Kalman滤波实现3种类型、 18个传感器数据的综合处理, 提高了数据的精度和可信度.

1 数据融合基本理论

1.1 小波变换阈值去噪

阈值去噪法的主要思想是由于数据和噪声经过小波变换后的数据具有不同的性质特征, 即真实数据自身的能量相对应的小波系数幅度偏大, 而干扰噪声的小波系数幅度偏小. 满足x≥λ,x表示小波分解系数,λ表示设定的阈值. 去噪步骤如下:

1) 对带噪信号f(t)进行小波变换, 将信号分解为多层, 每层对应的系数为ωj,k.

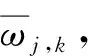
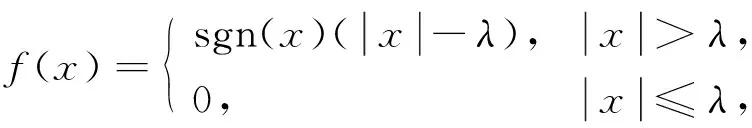
(1)

其中sgn(x)为符号函数. 阈值的选取采用局部适应阈值, 本文选取阈值为3α, 即把每层小波变换后的系数按大小排列, 然后取其中位数, 最后把中位数除以0.674 5即得到相应层所在的α. |x|>3α由信号产生, 而|x|≤3α由噪声产生.

1.2 Kalman滤波

Kalman滤波器的核心内容是假设需要预测的为t时刻的值, 根据其滤波器, 可通过上一时刻的最优结果预测出现在的值为

Y(t|t-1)=AY(t-1|t-1)+BU(t),

(2)

其中：Y(t|t-1)表示通过上一时刻的最优结果预测出现在的值；Y(t-1|t-1)表示上一状态的最优结果；U(t)是控制量；A和B是系统参数. 当Y(t|t-1)更新时, 其信任尚未更新, 用T表示为

T(t|t-1)=AT(t-1|t-1)A′+Q,

(3)

其中:Y(t|t-1)和Y(t-1|t-1)的信任分别为T(t|t-1)和T(t-1|t-1)；A′表示A的转置矩阵; Q表示高斯白噪声的信任. t时刻的最佳融合值Y(t|t)为

Y(t|t)=Y(t|t-1)+Kg(t)(Z(t)-HY(t|t-1)),

(4)

其中: Z(t)表示t时刻的测量值; H是测量系统的参数; Kg表示Kalman增益, 其表达式为

(5)

最优的估算值Y(t|t)对应的信任更新为

T(t|t)=(1-Kg(t)H)(t|t-1).

(6)

1.3 信噪比融合

1.3.1 贴近度矩阵 假设系统中有n个传感器, 用这些传感器对同一事物对象的某种特征进行测量, 假设传感器i在k时刻的采集值为xi(k)(i=1,2,…,n), 把各观测值的全体视为一个模糊集, 即用非精确的数据描述对象.

定义1时间为k时, 节点i与j测量值的支撑力度公式为

(7)

定义2时间为k时, 各节点间的支持度矩阵为

(8)

定义3时间为k时, 传感器i与其他传感器的支持度为

(9)

1.3.2 信噪比融合方法 一致性测度ri(k)仅反映了在某个测量时间, 节点i的测量值与所有传感器节点测量值的相近水平. 单个时刻ri(k)的值, 并不代表在整个时间区间上传感器节点的可靠性, 应考虑到整个测量时间区间上传感器节点的可靠性, 定义第k时刻第i个传感器节点观测的均值和方差分别为

(10)

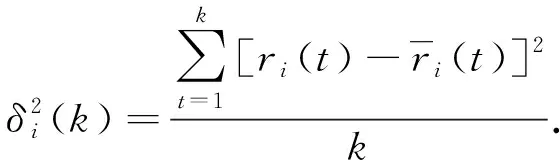
(11)

若某节点的采集信号平均值较大, 且信号的波动较小, 则节点较稳定, 具有较高的支持度, 该节点的权重较高. 因此可用信噪比描述节点的支持度, 信噪比的值为平均值除以信号波动的方差.

定义4时间为k时, 传感器i的支持度wi(k)为

(12)

归一化后为

(13)

信噪比的测度不包含变化的参数, 避免了主观因素对数据融合的影响, 能更真实地还原各传感器节点对所测对象的状态特征, 较好地度量了各传感器在融合中所占的不同权重. 本文的数据融合是通过传感器的一致可靠性度量, 所有传感器节点在k时刻测量值融合后的数据为

(14)

2 改进融合方法

所有的传感器节点采用分布式随机部署在一定区域, 且自形成一个传感器网络, 实现对传感数据的采集. 采用nesC语言编程实现, 操作系统为TinyOS, 实现数据的多步跳转和传输, 最后通过Sink节点把数据汇集到后台数据库中. 本文主要对后台收集的数据进行分析、 处理和融合, 数据的处理和融合过程如图1所示.

图1 数据的处理和融合过程Fig.1 Processing and fusion process of data

融合过程步骤如下：

1) 利用小波技术对各传感器采集的数据去除高斯白噪声, 其中包括数据清理、 数据变换和数值规约；

2) 利用小波技术对数据进行压缩；

3) 利用小波技术对预处理过后的数据进行分层, 对分层后的相似高频系数及细节低频系数进行Kalman滤波；

4) 利用最大最小贴近度对传感器数据计算信噪比, 通过信噪比对数据的近似系数进行融合；

5) 利用小波技术重构数据, 得到融合结果.

2.1 数据预处理

通过不同的填值方式填补缺失值, 去除对最终决策无关的属性数据和光滑噪声, 利用距离等方法识别离群的数据点并对其进行纠正, 步骤如下.

1) 数据清理： 通过偏差检测进行数据清洗.

2) 数据变换： 主要操作包括数据的归一化, 归一化过程为

(15)

其中:v是测得的一个数据; max和min分别是整个测量过程中的最大、 最小值. 式(15)是将数据v映射至区间[new_min,new_max]上.

3) 数值归约： 减少数据量过程, 可将原始数据量统一变小.

2.2 小波压缩

小波分析对一维信号进行压缩主要包括以下步骤：

1) 一维信号通过小波变换分解为多层, 包括高频系数和低频系数;

2) 对低频系数即细节系数(包含数据的大部分噪声)进行阈值化处理, 对不同层的细节系数可选择不同的阈值进行处理;

3) 对阈值量化处理后的系数进行小波重构.

2.3 小波分层及Kalman滤波

基于小波变换和Kalman滤波算法的基本思路如下：

1) 基于小波变换的多分辨率分析方法, 对信号进行多尺度分解；

2) 用Kalman滤波器估计每个尺度上的数据, 并得到每个尺度上的估计结果;

3) 基于每个尺度上的估计结果, 通过Mallat的快速重建算法, 获得原始信号的融合结果.

3 实验结果及分析

3.1 数据来源

本文利用温湿度传感器、 pH传感器和溶解氧传感器对湖的数据进行采集, 图2为3种传感器节点示意图.

1) 温湿度传感器： 如图2(A)所示, 其为数字温湿度传感器, 湿度模块和温度模块共同工作(本文只处理温度数据), 利用电阻式测量湿度模块, 利用热敏电阻测量温度模块, 温湿度传感器具有质地优越、 响应快速、 抗干扰能力强等优点. 对每个温湿度传感器都进行了校准, 传感器体积小, 采集数据过程消耗的能量低, 传输距离可达20 m以上, 可应用于复杂的环境. 节点每30 s收集一次环境值.

2) pH传感器： 其原理是测量被测物体中的H+浓度(氢离子浓度), 并把H+浓度转变成可输出的数据, 其主要用于生活的水域, 如图2(B)所示, 传感器每隔30 s采集一次数据.

3) 溶解氧传感器： 溶解氧质量浓度指示水的质量, 如图2(C)所示, 传感器每隔30 s采集一次数据.

图2 传感器节点示意图Fig.2 Schematic diagram of sensor node

将6个温湿度传感器、 6个pH传感器、 6个溶解氧传感器共18个传感器节点均匀部署在南昌航空大学后湖中, 每个传感器间隔30 s进行一次数据采集并传输, 每个传感器连续收集24 h共2 880条数据, 并随机选择其中部分数据作为实验数据进行处理分析, 以验证本文算法的有效性. 上述传感器对应的数据单位、 采集时间间隔、 采集数据个数、 采集数据范围和精确度等实验数据的属性列于表1.

表1 传感器数据属性

3.2 数据预处理结果

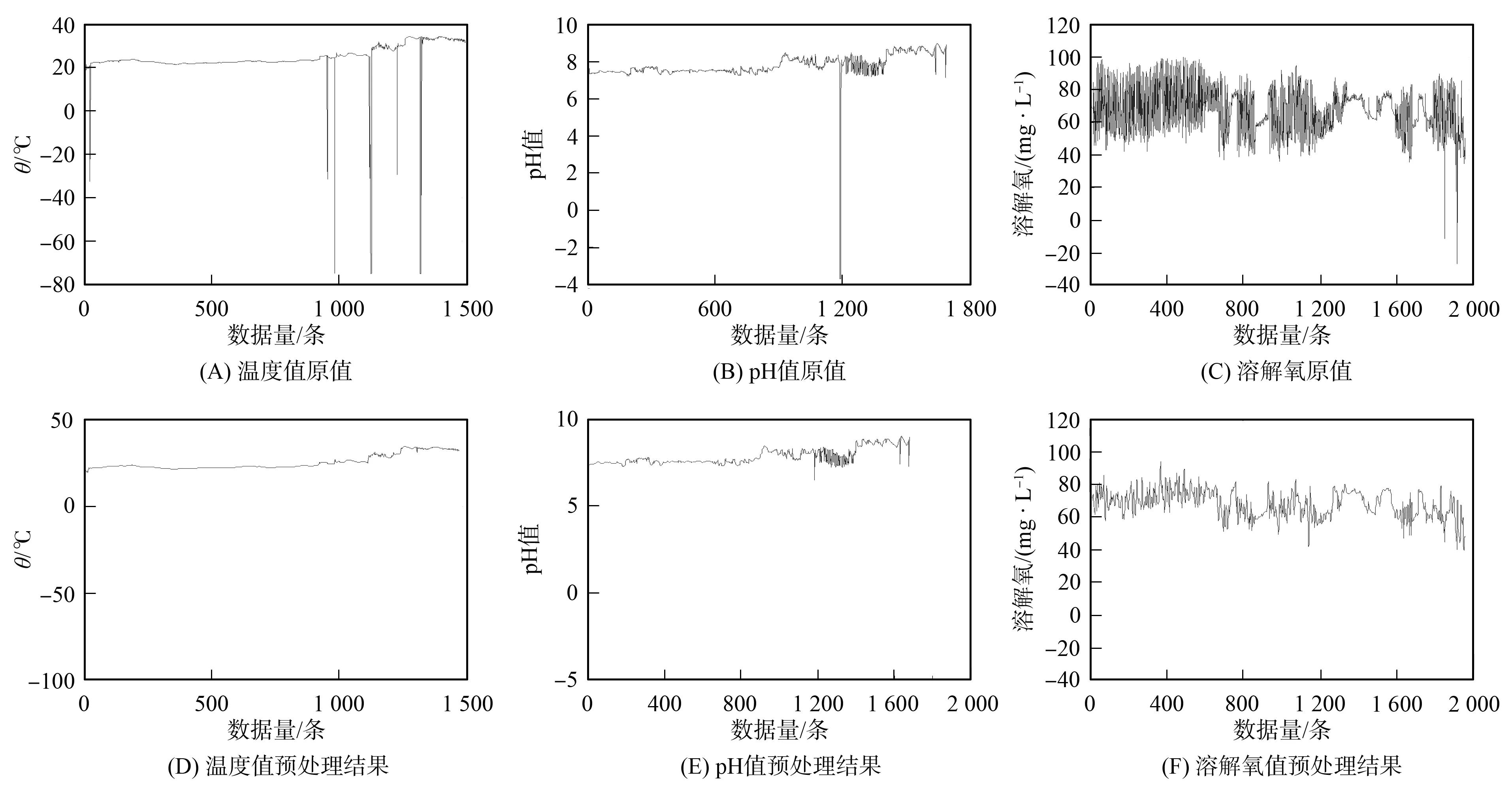
图3 温度值、 pH值、 溶解氧值预处理效果对比Fig.3 Comparison of pretreatment effects of temperature value, pH value and dissolved oxygen value

分别选取3种类型的传感器节点各一个, 利用小波去噪对其数据进行预处理, 温度值、 pH值和溶解氧数据预处理的结果如图3所示. 由图3可见, 3种类型的原始数据间的偏差震荡均较大, 表明原始序列数据中存在异常值或噪声, 经过小波技术预处理后, 有效地剔除了异常值或噪声, 数据曲线变得更平滑, 且序列数据相对稳定, 效果显著.

3.3 小波压缩结果

在对数据进行预处理剔除噪声后, 下面将对小波压缩结果进行分析. 分别选取3种类型的传感器节点各一个, 利用小波压缩处理后的结果如图4所示. 由图4可见, 每个小时间段只存储一个值, 减少了内存的使用及数据的传输, 易于数据存储, 数据波动较大的, 压缩后有再次去噪的效果, 压缩后的曲线光滑, 效果显著.

图4 温度值、 pH值、 溶解氧值小波压缩处理效果Fig.4 Wavelet compression treatment effects of temperature value, pH value, dissolved oxygen value

3.4 小波分层及Kalman滤波

在对数据进行压缩后, 对小波分层级及Kalman滤波结果进行分析. 本文选择6个溶解氧传感器节点中的1号溶解氧传感器节点数据作为分析的样本, 滤波效果如图5所示. 数据分析采用母小波“db5”, 将数据分为5层. 由图5可见, Kalman滤波后数据所对应的曲线更光滑, 近似系数层是基本内容, 经过小波分层后近似系数层本身噪声较小, 多数噪声被分到了细节系数层, 将噪声向左右两边趋近.

3.5 数据融合结果

本文对18个传感器数据进行融合结果分析, 其中, 温度、 pH值和溶解氧传感器节点数据的融合结果如图6所示, 其中： (A),(B),(C)分别为温湿度传感器、 pH传感器和溶解氧传感器全部实验数据的融合结果; (D)为放大了(A)中编号为495～510之间16个数据的融合结果, 黄色、 青色、 黑色、 绿色、 紫色和蓝色曲线分别表示1～6号传感器节点在495～510时间段采集的数据曲线, 红色曲线表示6个传感器节点在495～510时间段采集的数据融合后的曲线; (E)为放大了(B)中编号为614～626之间13个数据的融合结果, 黄色、 青色、 黑色、 绿色、 紫色和蓝色曲线分别表示1～6号传感器节点在614～626时间段采集的数据曲线, 红色曲线表示传感器节点在614～626时间段采集的数据融合后的曲线； (F)为放大了(C)中编号为1 390～1 407之间18个数据的融合结果, 黄色、 青色、 黑色、 绿色、 紫色和蓝色曲线分别表示1～6号传感器节点在1 390～1 407时间段采集的数据曲线, 红色曲线表示传感器节点在1 390～1 407时间段采集的数据融合后的曲线.

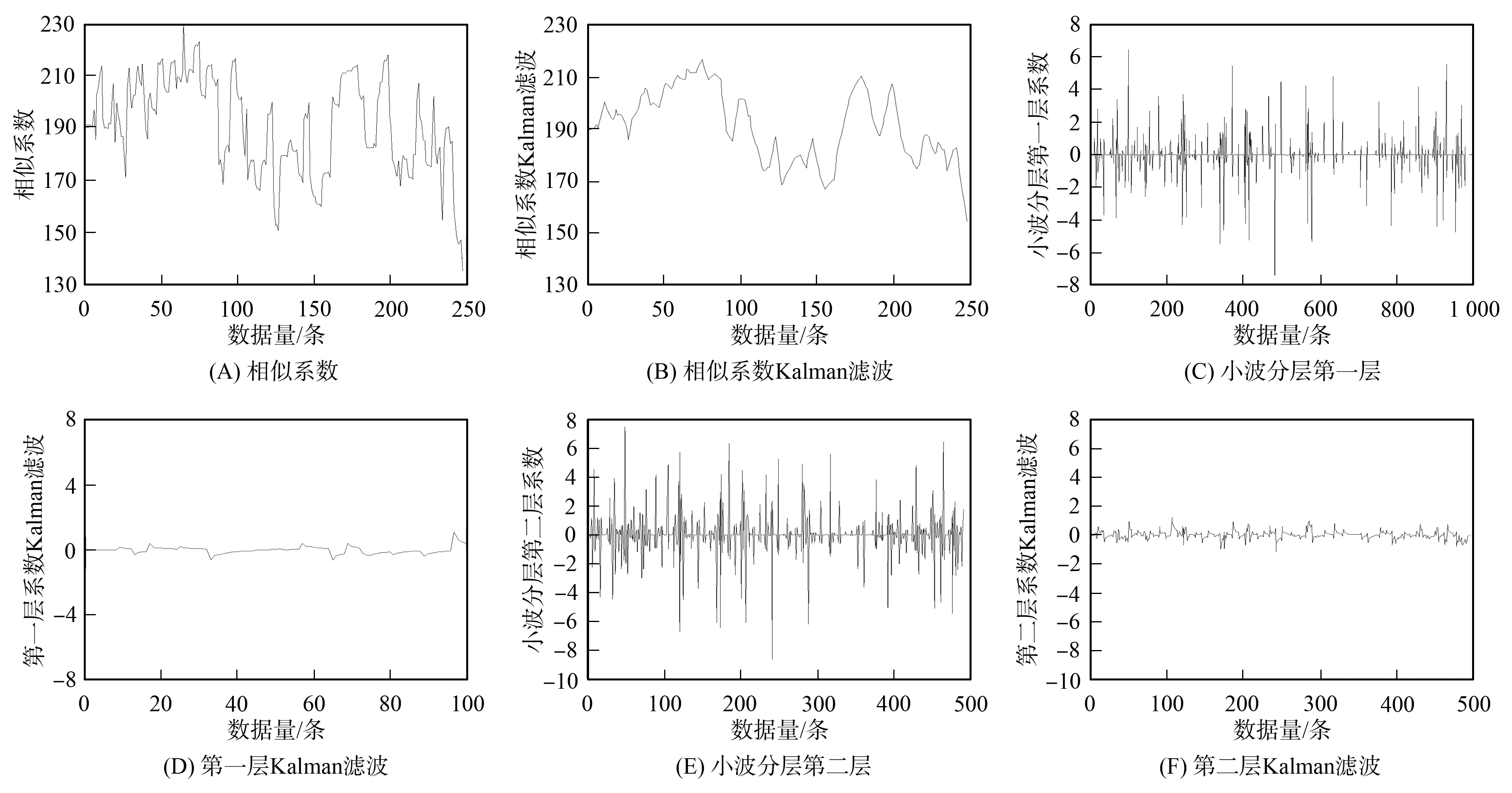
图5 溶解氧数据的小波分层及Kalman滤波效果Fig.5 Effects of wavelet stratification and Kalman filtering for dissolved oxygen data

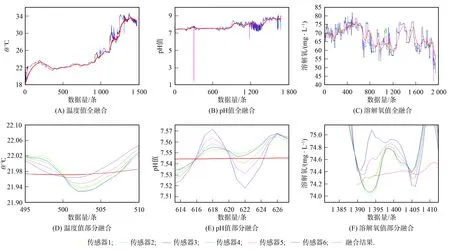
图6 温度值、 pH值和溶解氧传感器数据的融合结果Fig.6 Fusion results of temperature value, pH value and dissolved oxygen sensor data

由图6可见, 本文提出的数据融合算法波动性较小, 稳健性强. 这是因为信噪比的测度不包含变化的参数, 避免了主观因素对数据融合的影响, 能更真实地还原各传感器节点对所测对象的状态特征, 较好地度量了各传感器在融合中所占的不同权重. 本文实验中, 自适应得到的各传感器节点的权重列于表2.

表2 传感器节点的权重

下面从均值、 方差、 均方差、 极差的大小对数据融合算法的稳健性进行评价. 温度值、 pH值和溶解氧值的比较结果分别列于表3～表5. 由表3～表5可见, 本文算法无论是针对全部数据还是部分数据, 相比于其他算法的性能均较好, 对比分析结果表明了本文方法的稳健性.

表3 不同算法对温度值的性能对比

表4 不同算法对pH值的性能对比

表5 不同算法对溶解氧值的性能对比

综上所述, 本文在分析多种多传感器数据融合相关算法研究现状及优缺点的基础上, 提出了一种基于信噪比的小波Kalman滤波数据融合算法, 并针对多传感器节点在实际环境采集的数据进行了数据实验, 最后结合实验结果对不同融合算法进行对比分析. 实验结果表明：

1) 相比权值数据融合、 小波数据融合等算法, 基于信噪比的小波Kalman滤波数据融合算法的实现相对简单、 速度快, 信息保留效果好, 数据有较好的稳健性；

2) 前期的数据预处理对数据融合非常关键, 预处理的结果直接影响后面的融合效果；

3) 对于数据方差较大的情况, 本文方法的融合效果更好.