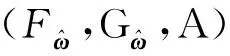一种新的双犹豫模糊软集及其在决策问题中的应用
2018-10-09郭建胜
郭 建 胜
(陕西师范大学 数学与信息科学学院, 西安 710119)
软集理论[1]可处理不确定性问题, 其目的是解决模糊数学参数化方法理论中存在的缺陷. 目前, 关于软集的研究已有许多结果[2-10].
在考虑参数集时, 可以同时考虑这些参数集的“非参数集”, 因此, 文献[11-12]提出了双软集和模糊双软集的概念; 文献[13-15]提出了犹豫模糊集的概念; 文献[14]将犹豫模糊集和粗糙集相结合, 给出了结构化方法和公理化方法; 文献[16]将双犹豫模糊集的非隶属度与软集的参数化特性相结合, 提出了双犹豫模糊软集(F,A)的概念, 即对域集U, 参数集E,A⊆E, 存在映射F,F为从A到U的双犹豫模糊集的映射. 本文将双软集模型和犹豫模糊集相结合, 建立一种新的软集模型, 称为双犹豫模糊软集. 与文献[16]中概念的区别为在A和A上, 分别建立从A和A到U的犹豫模糊集的映射F:A→HF(U)和G:A→HF(U). 与模糊软集及其经典的推广相比, 本文定义的双犹豫模糊软集不仅能反映对关注对象参数选择的犹豫性, 也能反映所选择参数的“非参数性”.
1 预备知识
若无特殊说明, 本文中的论域U一般指非空有限集.
定义1[1]设U为初始论域,E为参数集,P(U)为U的幂集,A⊆E,F:A→P(U)为映射, 则称序对(F,A)为U上的一个软集.
例1假设域集U是5套房子的集合, 记为U={h1,h2,h3,h4,h5}.A={e1,e2,e3,e4,e5}是参数的集合, 其中e1,e2,e3,e4,e5分别表示参数“便宜”、 “漂亮”、 “木质的”、 “面积大”和“绿化好”. 软集(F,A)可用于描述顾客对房子的评价. 假设F(e1)={h1,h4},F(e2)={h2,h3},F(e3)={h2,h4,h5},F(e4)={h1,h4,h5},F(e5)={h3}, 则软集(F,A)是一个参数族{F(ei); 1≤i≤5}, 其为U的子集. 其中F(e1)={h1,h4}表示房子h1和h4是“便宜的”, 其他类似. 于是软集(F,A)表示为
(F,A)={(e1,{h1,h4}),(e2,{h2,h3}),(e3,{h2,h4,h5}),(e4,{h1,h4,h5}),(e5,{h3})}.
为了在计算机上存储软集, 表1列出了例1中定义软集的列表表示.

表1 例1中软集(F,A)的列表表示

定义3[13]设U是非空域集, 则通过一个函数hA(x):U→P([0,1]), 可在域集U上定义一个犹豫模糊集为
A={〈x,hA(x)〉:x∈U},
其中hA(x)是函数值在[0,1]区间上的函数, 表示元x∈U对集合A可能的关系度. 为方便, 称hA(x)为一个犹豫模糊元.
例2设U={x1,x2,x3}是域集,hA(x1)={0.3,0.4,0.8},hA(x2)={0.4,0.5},hA(x3)={0.2,0.4,0.8,0.9}是犹豫模糊元, 则犹豫模糊集为
A={〈x1,{0.3,0.4,0.8}〉,〈x2,{0.4,0.5}〉,〈x3,{0.2,0.4,0.8,0.9}〉}.

注1由于不同犹豫模糊元中值的个数不同, 所以用l=l(hA(x))表示犹豫模糊元hA(x)中值的个数. 由文献[13]可知:
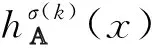
2) 对于两个犹豫模糊元hA(x)和hB(x), 如果l(hA(x))≠l(hB(x)), 则l=max{l(hA(x)),l(hB(x))}.
为了进行比较, 两个犹豫模糊元hA(x)和hB(x)应有相同长度l, 所以如果hA(x)中的元少于hB(x)中的元, 则将hA(x)中元的个数进行扩充, 即将hA(x)中的最大元重复增加, 直到其中元的个数与hB(x)中元的个数相同为止.
本文用到的其他有关犹豫模糊集的概念和符号参见文献[13-15].
定义4[13]设U是一个非空的有限域集. 对任意的A,B∈HF(U)和任意的x∈U, 定义
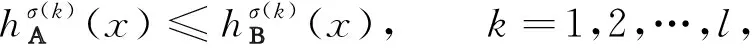
定义5[13]设U是非空有限域集, A和 B是两个犹豫模糊集, 则对任意的x∈U:
1) A的补记为Ac, 即

h(x)=h

h(x)=hA(x)⊕
h(x)=hA(x)⊗
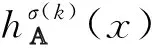
定理1[13]设U是非空有限域集. 如果 A和 B是两个犹豫模糊集, 则:

定义6[17]设U为非空域集,E为非空参数集,HF(U)为U的所有犹豫模糊集的全体,A⊆E,F:A→HF(U)为映射, 则称(F,A)为U上的一个犹豫模糊软集.
定义7设U为非空集,A⊆U, 则称三元组(F,G,A)为U上的双犹豫模糊软集, 其中F和G是映射,F:A→HF(U),G:A→HF(U), 使得对所有的x∈U, 有(x)+(x)≤1,k=1,2,…,l, 其中l=max{l(hF(e)(x)),l(hG(e)(x))}.
例3设U是4套房子的集合, 记为U={x1,x2,x3,x4}. 设A是一个参数集, 其中A={e1,e2,e3}={便宜,漂亮,木质的}. 假设某人考虑的某套房子xj与参数ei间的隶属度很难精确表达, 为解决该问题, 他把房子xj和参数ei之间的隶属度用若干可能的值表示, 则双犹豫模糊软集S=(F,G,A)定义如下:
表2列出了例3中定义的双犹豫模糊软集的列表表示.

表2 例3中双犹豫模糊软集(F,G,A)的列表表示
定义8对于U上的两个双犹豫模糊软集(F,G,A)和(F1,G1,B), 如果满足:
1)A⊆B;

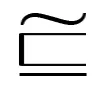
定义9设(F,G,A)和(F1,G1,B)是域集U上的两个双犹豫模糊软集, 如果(F,G,A)和(F1,G1,B)满足下列条件:

则称(F,G,A)和(F1,G1,B)相等, 记为(F,G,A)=(F1,G1,B).
定义10称(F,G,A)c=(Fc,Gc,A)为双犹豫模糊软集(F,G,A)的补, 其中Fc和Gc是映射, 且对任意的e∈A, 有Fc(e)=G(e),Gc(e)=F(e).
显然, 有((F,G,A)c)c=(F,G,A).
定义11如果对任意的e∈A, 有Φ(e)=Ø和U(e)=U, 则称U上的双犹豫模糊软集为相对空双犹豫模糊软集, 记为(Φ,U,A).
定义12如果对任意的e∈A, 有U(e)=U和Φ(e)=Ø, 则称U上的双犹豫模糊软集为相对完全双犹豫模糊软集, 记为(U,Φ,A).
易得:
命题1如果(Φ,U,A)是一个相对空双犹豫模糊软集, 则(Φ,U,A)c=(U,Φ,A)是一个相对完全双犹豫模糊软集; 如果(U,Φ,A)是一个相对完全双犹豫模糊软集, 则(U,Φ,A)c=(Φ,U,A)是一个相对空双犹豫模糊软集.
定义13设(F,G,A)和(F1,G1,B)是U上的两个双犹豫模糊软集, 则其交运算定义为(F,G,A)∧(F1,G1,B), 即
(F,G,A)∧(F1,G1,B)=(H,K,A×B),
其中对任意的(α,β)∈A×B, 有

定义14设(F,G,A)和(F1,G1,B)是U上的两个双犹豫模糊软集, 则其并运算定义为(F,G,A)∨(F1,G1,B), 即
(F,G,A)∨(F1,G1,B)=(M,N,A×B),
其中对任意的(α,β)∈A×B, 有M(α,β)=F(α)F1(β), N(α,β)=G(α)G1(β).
定理2设(F,G,A)和(F1,G1,B)是U上的两个双犹豫模糊软集, 则下列等式成立:
1) ((F,G,A)∧(F1,G1,B))c=(F,G,A)c∨(F1,G1,B)c;
2) ((F,G,A)∨(F1,G1,B))c=(F,G,A)c∧(F1,G1,B)c.
证明: 1) 设((F,G,A)∧(F1,G1,B))=(H,K,A×B), 则由定义10和定义13, 有
((F,G,A)∧(F1,G1,B))c=(H,K,A×B)c=(Hc,Kc,A×B),
其中对任意的x∈U和(α,β)∈A×B, 有
由定理1知,
另一方面, 由定义10和定义14, 有
其中对任意的x∈U和(α,β)∈A×B, 有
因此(Hc,Kc,A×B)=(M,N,A×B).
2) 类似可证.
定理3设(F,G,A),(F1,G1,B)和(F2,G2,C)是U上的3个双犹豫模糊软集, 则下列等式成立:
1) (F,G,A)∧((F1,G1,B)∧(F2,G2,C))=((F,G,A)∧(F1,G1,B))∧(F2,G2,C);
2) (F,G,A)∨((F1,G1,B)∨(F2,G2,C))=((F,G,A)∨(F1,G1,B))∨(F2,G2,C);
3) (F,G,A)∧((F1,G1,B)∨(F2,G2,C))=((F,G,A)∧(F1,G1,B))∨((F,G,A)∧(F2,G2,C));
4) (F,G,A)∨((F1,G1,B)∧(F2,G2,C))=((F,G,A)∨(F1,G1,B))∧((F,G,A)∨(F2,G2,C)).
证明: 1) ∀x∈U, α∈A, β∈B及γ∈C, 有
且
G(γ)(x))=(G(γ)(x),
所以(F,G,A)∧((F1,G1,B)∧(F2,G2,C))=((F,G,A)∧(F1,G1,B))∧(F2,G2,C)成立. 2),3),4)类似可证.
定义15对任意的e∈C, 两个相同域集U上的双犹豫模糊软集(F,G,A)和(F1,G1,B)的扩张并定义为双犹豫模糊软集(H,K,C), 记为(F,G,A)∪E(F1,G1,B)=(H,K,C). 其中: C=A∪B;
K(
定义16对任意的e∈C, 两个相同域集U上的双犹豫模糊软集(F,G,A)和(F1,G1,B)的扩张交定义为双犹豫模糊软集(H,K,C), 记为(F,G,A)∩E(F1,G1,B)=(H,K,C). 其中: C=A∪B;
K(
定义17对任意的e∈C, 两个相同域集U上的双犹豫模糊软集(F,G,A)和(F1,G1,B)的限制并定义为双犹豫模糊软集(H,K,C), 记为(F,G,A)∪R(F1,G1,B)=(H,K,C). 其中: C=A∩B非空;
H(e)=F(e)F1(e);K(e)=G(e)G1(e).
定义18对任意的e∈C, 两个相同域集U上的双犹豫模糊软集(F,G,A)和(F1,G1,B)的限制交定义为双犹豫模糊软集(H,K,C), 记为(F,G,A)∩R(F1,G1,B)=(H,K,C). 其中: C=A∩B非空;

特别地, 如果A∩B=Ø, 则规定(F,G,A)∩R(F1,G1,B)=(Φ,U,Ø)=(F,G,A)∪R(F1,G1,B).
例4假设域集U上的双犹豫模糊软集(F,G,A)和(F1,G1,B)如例3所示, 则由定义15~定义18可知, (F,G,A)和(F1,G1,B)的扩张并、 扩张交、 限制并、 限制交双犹豫模糊软集(H,K,C)的列表表示分别列于表3~表6.

表3 (F,G,A)和(F1,G1,B)的扩张并双犹豫模糊软集(H,K,C)的列表表示

表4 (F,G,A)和(F1,G1,B)的扩张交双犹豫模糊软集(H,K,C)的列表表示

表5 (F,G,A)和(F1,G1,B)的限制并双犹豫模糊软集(H,K,C)的列表表示

表6 (F,G,A)和(F1,G1,B)的限制交双犹豫模糊软集(H,K,C)的列表表示
显然有:
引理1设(F,G,A),(F1,G1,B)和(F2,G2,C)是域集U上的3个双犹豫模糊软集, 则对任意的∘∈{∩E,∩R,∪E,∪R}, 下列等式成立:
1) (F,G,A)∘((F1,G1,B)∘(F2,G2,C))=((F,G,A)∘(F1,G1,B))∘(F2,G2,C);
2) (F,G,A)∘(F1,G1,B)=(F1,G1,B)∘(F,G,A).
引理2设(Φ,U,A)和(U,Φ,A)分别为相对空与相对完全双犹豫模糊软集, (F,G,A)和(F1,G1,A)是共同域集U上的双犹豫模糊软集, 则:
1) (F,G,A)∪E(F1,G1,A)=(F,G,A)∪R(F1,G1,A);
2) (F,G,A)∩E(F1,G1,A)=(F,G,A)∩R(F1,G1,A);
3) (F,G,A)∪E(F,G,A)=(F,G,A)∪R(F,G,A)=(F,G,A);
4) (F,G,A)∩E(F,G,A)=(F,G,A)∩R(F,G,A)=(F,G,A);
5) (F,G,A)∪E(Φ,U,A)=(F,G,A)∪R(Φ,U,A)=(F,G,A);
6) (F,G,A)∩E(U,Φ,A)=(F,G,A)∩R(U,Φ,A)=(F,G,A).
引理3设(F,G,A)和(F1,G1,B)是相同域集U上的两个双犹豫模糊软集, 则:
1) ((F,G,A)∪E(F1,G1,B))c=(F,G,A)c∩E(F1,G1,B)c;
2) ((F,G,A)∩E(F1,G1,B))c=(F,G,A)c∪E(F1,G1,B)c;
3) ((F,G,A)∪R(F1,G1,B))c=(F,G,A)c∩R(F1,G1,B)c;
4) ((F,G,A)∩R(F1,G1,B))c=(F,G,A)c∪R(F1,G1,B)c.
2 双犹豫模糊软集的约简
文献[18]介绍了区间值模糊软集约简的概念. 本文将其应用到双犹豫模糊软集上, 并通过约简的方法把双犹豫模糊软集变为双模糊软集.
定义19设(F,G,A)是域集U上的双犹豫模糊软集, 使得对任意的e∈A, F(e)和G(e)是犹豫模糊集. 对任意的x∈U,

(1)
其中l=l(hA(x))表示犹豫模糊元hA(x)中元的个数. 则定义域集U上的双模糊软集(F-,G-,A)定义为

称为(F,G,A)的悲观约简双模糊软集.
定义20设(F,G,A)是域集U上的双犹豫模糊软集, 对任意的e∈A, F(e)和G(e)是犹豫模糊集. 对任意的x∈U, 式(1)成立, 其中l=l(hA(x))表示犹豫模糊元hA(x)中元的个数. 则域集U上的双模糊软集(F+,G+,A)定义为F+(e)={〈x,(x)〉: x∈U}, G+(e)= {〈x,(x)〉: x∈U}, ∀e∈A, 称为(F,G,A)的乐观约简双模糊软集.
定义21设(F,G,A)是域集U上的双犹豫模糊软集, 对任意的e∈A, F(e)和G(e)是犹豫模糊集. 对任意的x∈U, hF(e)(x)={(x), k=1,2,…,l}, h(x)={(x), k=1,2,…,l}, 其中l=l(hA(x))表示犹豫模糊元hA(x)中元的个数. 则域集U上的双模糊软集(FN,GN,A)定义为
称为(F,G,A)的均值约简双模糊软集.
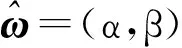



例5考虑例3中的双犹豫模糊软集, 计算表2中双犹豫模糊软集(F,G,A)的悲观约简双模糊软集(F-,G-,A)、 乐观约简双模糊软集(F+,G+,A)及均值约简双模糊软集(FN,GN,A), 结果分别列于表7~表9.

表7 双犹豫模糊软集(F,G,A)的悲观约简双模糊软集(F-,G-,A)

表8 双犹豫模糊软集(F,G,A)的乐观约简双模糊软集(F+,G+,A)

表9 双犹豫模糊软集(F,G,A)的均值约简双模糊软集(FN,GN,A)
3 基于相关系数的算法
设域集U={x1,x2,…,xn}, (F,G,A)是域集U上的一个双犹豫模糊软集, 下面计算其悲观约简双模糊软集(F-,G-,A)、 乐观约简双模糊软集(F+,G+,A)或者均值约简双模糊软集(FN,GN,A). 通过该方法, 将犹豫模糊集F(e),G(e)相应地变为模糊集. 此外, 若从双犹豫模糊软集中诱导出双模糊软集, 可参见文献[19]的算法, 得到最理想的选择. 下面给出基于双犹豫模糊软集的决策最优算法.
算法1基于双犹豫模糊软集的决策最优算法.
算法步骤如下:
1) 输入双犹豫模糊软集S =(F,G,A);

3) 输入模糊集λ: A→[0,1], μ: A→[0,1](或给出一对数值s,t∈[0,1]);


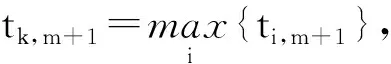
7) 如果有多个xk存在, 则选择xk中的任意一个即可, 也可回到步骤3), 重新调整模糊集λ,μ(或s,t), 然后继续计算.
例6考虑表8中的双犹豫模糊软集(F,G,A)的乐观约简双模糊软集(F+,G+,A). 取s=0.8, t=0.1, 计算双模糊软集(F+,G+,A)的(0.8,0.1)-水平截集. 对于参数e1, 计算模糊集F+(e1)和G+(e1)的(0.8,0.1)-水平截集, 可得U的分明子集为
L(〈F+(e1),G+(e1)〉;0.8,0.1)={x1,x4}.
结果表明, 以关系度s=0.8, t=0.1衡量, x1,x4属于漂亮的房子.
通过分析其他参数, 可得模糊集F+(ei),G+(ei)(i=2,3)的(0.8,0.1)-水平截集:

表10列出了水平截集L((F+,G+,A);0.8,0.1)的列表表示, 其中最后一列给出了每个对象的选择值. 由表10可见, 极大选择值为3, 所以最优决策选择是x4.

表10 (F+,G+,A)的(0.8,0.1)-水平截集及选择值c的列表表示
算法1的优点为: 首先, 易见算法1与文献[12,19]的算法相比, 具有更小的计算量. 算法1无需如文献[12,19]的算法建立比较列表, 只需建立水平双软截集中对象的选择值即可, 事实上, 算法1最后是在处理分明软集, 而不是最初的双犹豫模糊软集; 其次, 算法1是一个可调算法, 即当最后一步有太多“最优选择”时, 可返回步骤3)并检查调整所使用的截集数值λ,μ(或s,t), 以便调整最优选择xk.