分数阶Kuramoto-Sivashinsky方程的精确行波解

常 晶, 刘 洋, 高忆先

(1. 吉林农业大学 信息技术学院, 长春 130118; 2. 东北师范大学 数学与统计学院, 长春 130024)

时空分数阶非线性偏微分方程在化学、 生物学、 数学、 通信、 物理和工程等领域应用广泛. Kuramoto-Sivashinsky型方程(简称K-S型方程)在物理和工程等领域得到广泛关注, 目前, 关于求解K-S型方程解的研究已有许多结果[1-9], 如双曲正切函数法[1]、 高阶有限元法[2]、 Jacobi椭圆函数展开法[3]、 正切函数法[4]、 Riccati展开法[5]、 Lie对称法[6]等. 本文主要考虑具有物理背景的时空分数阶K-S型方程的精确行波解, 利用具有两个变量(G′/G,1/G)-函数展开法, 得到了K-S型方程的双曲函数形式、 三角函数形式和有理函数形式的精确行波解.

1 (G′/G,1/G)-函数展开法

考虑一般的分数阶非线性偏微分方程:

(1)

其中: u=u(x,t); 0<α,β≤1, 且α的Riemann-Liouville分数阶导数为

(2)

(G′/G,1/G)-函数展开法步骤如下:

Q(U,U′,U″,…)=0.

(3)

2) 不妨设方程(3)具有下列形式的行波解：

(4)

其中: φ=G′/G, ψ=1/G, G=G(ξ)为二阶常微分方程

G″(ξ)+λG′(ξ)=μ

(5)

的解; ai(i=0,1,…,N), bi(i=1,2,…,N), λ,μ均为待定常数; 正整数N为参数, 可通过平衡方程(1)中的最高阶非线性项与最高阶导数项确定. 方程(5)的解有下列3种形式:

① 当λ<0时, 方程(5)的解为

(6)

② 当λ>0时, 方程(5)的解为

(7)

③ 当λ=0时, 方程(5)的解为

G(ξ)=μξ2/2+A1ξ+A2,

(8)

3) 将式(4)代入式(3), 并令φ,ψ的同次幂系数为零, 可得关于参数ai(i=0,1,…,N), bi(i=1,2,…,N), λ,μ,A1,A2的代数方程组, 利用Mathematica科学计算软件, 可得这些参数的解, 进而可得方程(1)的精确行波解.

注1一个变量G′/G-函数展开法的关键是将偏微分方程的精确行波解转化为关于G′/G的多项式形式； 而两个变量(G′/G,1/G)-函数展开法是将偏微分方程的精确行波解转化为关于两个变量G′/G和1/G的多项式形式.

2 应 用

考虑如下分数阶K-S方程:

(9)

其中: 0<α≤1; β,γ,δ为任意常数. 为得到方程(9)的精确行波解, 假设u(x,t)为式(4)的形式, 且令

φ=G′/G,ψ=1/G

(10)

-cU′+βkU′+γk2U″+δkUU′=0.

(11)

由平衡方程(11)中导数的最高阶项与非线性最高阶项知N=1. 即

U=a0+a1φ+b1ψ,a1≠0.

(12)

于是由方程(5)解的3种形式, 可对方程(9)的解进行如下讨论.

情形1) 当λ<0时, 将式(12)代入方程(11), 并利用式(6), 且令φ,ψ的同次幂系数为零, 可得

利用Mathematica软件, 可得:

情形2) 当λ>0时, 将式(12)代入方程(11)中, 并利用式(6), 可得如下方程组:

利用Mathematica软件, 可得:

情形3) 当λ=0时, 同理可得如下方程组:

利用Mathematica软件, 可得:

其中c,k,μ是任意常数. 则方程(9)有理函数形式的行波解为

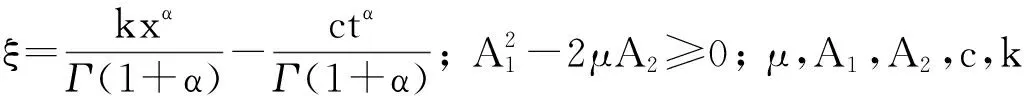
综上所述, 本文利用(G′/G,1/G)-展开法得到了具有物理背景的分数阶时-空非线性K-S型方程双曲函数行波解、 三角形式行波解以及有理函数形式的行波解. 结果表明, 该方法简单有效, 并可用于求解其他分数阶非线性发展方程的行波解.