“无心插柳”与“有意栽花”——例谈活用教材培养学生符号意识的策略思考

□北京市中关村第一小学 董文彬

在整个小学数学教学中，我们无疑应该重视发展学生的符号意识。而很多教师认为，符号意识应该是在学生学完“用字母表示数”真正跨入代数思维之后要做的事。其实不然，符号意识的培养应该贯穿于小学数学教学的整个六年“数与代数”的始终，特别是在学习“用字母表示数”方程单元之前，更应该注重学生前期符号意识的渗透与发展。下面以北师大版教材三年级上册为例，谈谈我在活用教材中培育学生符号意识的几点做法和思考。

一、前期对符号意识的两点思考

1.什么是符号意识？

培育和发展学生的符号意识，首先要弄清楚什么是符号意识。符号意识是整个数学课程内容教学的方向或目标之一，是学生必须具备的数学学科核心素养之一。到底什么是符号意识？《义务教育数学课程标准（2011年版）》明确指出了“符号意识”涵盖的三方面：1.能够理解并且运用符号表示数、数量关系和变化规律；2.知道使用符号可以进行运算和推理，得到的结论具有一般性；3.理解符号的使用是数学表达和数学思考的重要形式。

我们知道，每一个数学符号都有它特定的含义，例如＋、－、×、÷分别表示特定的运算意义，＝、≈、表示数学对象之间的某种关系，（）、［］表示运算顺序，图形符号、字母可以表示数、数量关系等。教学中让学生理解符号的意义是数学学习中最基本的要求，也是发展符号意识的最基本的要求。总而言之，学生一要能懂，二要会用。

2.符号思考的价值是什么？

符号，作为一种数学语言，可以表示数、数量关系和变化规律；作为一种数学工具，能够进行运算和推理，得到的结论具有一般性；作为一种数学方法，符号的使用是数学表达和进行数学思考的重要形式。而发展符号意识最重要的是运用符号进行数学思考，可称之为“符号思考”，这种思考是数学抽象、数学推理、数学模型等基本数学思想的集中反映，是最具数学特色的思维方式。教学中，教师应该创设一切契机帮助学生感受符号作为数学语言、数学工具、数学方法的独特价值。运用符号无论是表示数、数量关系和变化规律，还是进行运算和推理，亦或是进行数学思考和数学表达，核心都是对关系的集中刻画和反映，这种“关系”不同于运算的结果，获得的结论具有一般性和普遍性的特征。有时，什么条件都不提供，不需要直观看到，借助符号运用关系即可推理出这种一般性的数学模式，这是“数学人”不同于“其他人”的基本素养。

二、活用教材渗透培养符号意识的策略思考

1．“无心插柳”的精彩。

北师大版教材三年级上册第三单元“里程表（二）”一课，教材在呈现了“出租车里程表”例题之后，设计了这样一道有关“电表”的习题，帮助学生巩固理解同类问题的本质。

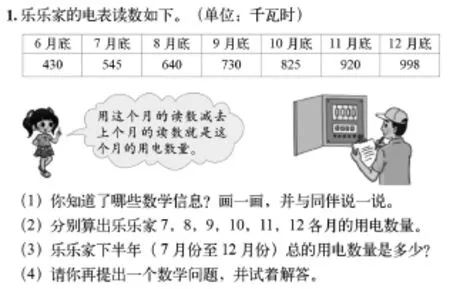
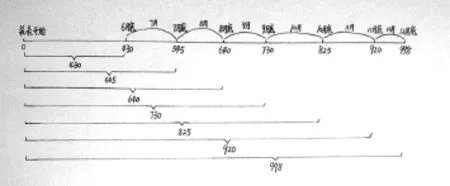
学生通过读取图表、画图理解（如下图）、分析数据，在解决第（3）问时最终呈现了如下两种解决问题的策略。

策略1:

7月：545－430＝115（千瓦时）

8月：640－545＝95（千瓦时）

9月：730－640＝90（千瓦时）

10月：825－730＝95（千瓦时）

11月：920－825＝95（千瓦时）

12月：998－920＝78（千瓦时）

下半年总用电量：115＋95＋90＋95＋95＋78＝568（千瓦时）。

策略2:

下半年总用电量：998－430＝568（千瓦时）。

通过交流、对比，学生发现：“策略1”是充分利用第（2）问的结果，思维简单但要付出计算繁琐的代价，“策略2”是借助几何直观，在图中寻求关系，用“12月底的电表读数”直接减去“6月底的电表读数”。比起“策略1”“策略2”更受学生欢迎，“策略2”帮助学生积累了解决此类问题的数学思维活动经验。

在汇报交流第（4）问的环节，精彩出现了！多数学生提出的问题都是“乐乐家用电量最多的是几月”“最少的是几月”“某月比某月的用电量多多少或少多少”之类。但此时一个学生提出的问题令大家瞠目结舌。

生1:乐乐家6月的用电量是多少千瓦时？

生2：（马上举手质疑）6月份的用电量没法求啊？

生3:这是个无效的问题！

生：对，6月的用电量根本没法算。

生1:（有些着急）可是我提的的确是个数学问题啊！

师：问得好，不急。6月的用电量能求吗？

生：不能求，缺条件。

师：如果要求“6月的用电量”，还需知道什么条件或信息？

生4:必须知道电表5月底的读数！

生:同意。

师：“5月底的读数”现在不知道，难道就不能求吗？

生：不能。

师：如果“5月底的读数”给了，怎么求？

生：用“6月底的读数”直接减去“5月底的读数”就可以了。

师：能不能想办法表示出“6月的用电量”是多少？

生5:如果5月底的读数是350，那么6月的用电量就是“430-350”。

生6:5月底的读数要是300，那6月的用电量就是“430-300”。

生7:这么说，如果5月底的读数要是200的话，那6月的用电量就是“430-200”了。

师：照这样，6月用电量的结果也不固定啊？可是你们看看7月到12月每个月的用电量是多少就是多少，这是怎么回事？

生：那是因为5月底的读数每次假设的都不一样。

师：我懂了。那你们能不能想办法用一种简洁、概括的方式表示出“6月的用电量”？尝试着写出来。

学生独立思考，尝试把自己的表示方法写出来，教师行间巡视，将学生典型的表示方法按序展示在屏幕上，引导全班汇报，交流分享。

生8:我写的是“430-5月底的读数”。

生10:啊？这样表示也行？

师：你们觉得这样行不行？

生：行。

生11:5月底的读数还可以用“x”表示，那6月的用电量就是“430-x”了。

师：太棒了！你们已经想到寻求用特定的符号来表示这个我们开始“无法求出的问题”了。大家看，（指生1）这位同学开始提出的问题还是不是无效的了？

生：不是。这个问题提得好，很有意义。

师：受这位同学启发，老师也提一个问题，乐乐家的电表明年1月底的读数是多少？能解决吗？试着写一写。

生13:我是这样表示的，“998＋a”，这里的a代表1月的用电量。

师：一个简单的符号“△”或字母“a”就可以表示出要解决的问题的答案，真是太奇妙了！数学的表达和思考就是这样简洁。

在上述两个问题的基础上，又有学生提出了新的问题：“乐乐家6月份到明年1月份总的用电数量是多少呢？该怎么表示呢？”本已平静的湖面又掀起了波澜。

生14:用“明年1月底的读数”减去“今年5月底的读数”不就就行了？

生15:可是这两个读数都不知道啊？

生16:我有办法！用“○”代表“今年5月底的读数”，用“△”代表“明年1月底的读数”，那么“△-○”就是“6月份到明年1月份总的用电数量”。

生：哦——

生17:假如“今年5月底的读数”用“x”代替，“明年1月底的读数”用“y”代替，那么“6月份到明年1月份总的用电数量”就可以用“y-x”表示。

此时，教室沸腾了，全班学生的脸上都洋溢着问题解决后成功的喜悦。

非常精彩，非常享受！恋恋不舍，不愿下课！可以说，这个“插曲”完全出乎我的意料，可谓“无心插柳柳成荫”，学生的表现也令我刮目相看。这是一节“跑偏”的课，这种“跑偏”的“精彩”起缘于“生1”最开始提出的那个令人“瞠目结舌”的备受质疑的“无效”的问题。在面对和解决这个问题的整个过程中，我没有回避，而是借助教材中的这道习题资源顺着学生的经验和思维而下，不断启发，不断引导，不断“挑事”，不断“拱火”，随机巧妙追问，激发学生在理解问题本质的基础上（能懂），自觉主动地用各种符号表示（未知的）数和数量关系（会用），即活用教材、学材，不回避，不躲藏，顺应思维，适当延伸，沿着问题的台阶，拾级而上，在潜移默化中自然穿插渗透和培养学生的符号意识。

2.“有意栽花”的丰实。

北师大版教材三年级上册“数学好玩”单元“日历中的规律”一课，教材设计了如下学习路径：按给出的一份某年9月份的日历，先观察日历中加框的4个数，寻找这4个数之间的关系，从不同的角度发现并表达其中蕴藏的普遍性的数学模式。同样地，再有序观察日历中有阴影的9个数，发现并表达其中蕴藏的一般性的数学规律。最后根据发现的日历中的模式或规律，通过“猜说生日”游戏，应用规律。

2014年第一次执教这节课时，笔者就注意到了这其中蕴藏的数学模式或数学规律，其实是一种抽象的共性关系的表达，这种数学表达的背后实际蕴含着符号思考的数学价值，即学生符号意识的培养。于是，我再次执教这节课时对这个环节放慢脚步，活用教材，精心预设，适当延伸，让学生体会符号作为数学语言和数学工具所具备的数学思考的价值，适时“见缝插针”，穿插渗透符号意识的培育和发展。教学片段如下：

出示日历（用方框在表中任意圈出4个日期）。

师：这是一份9月份的日历，用像这样的方框可以在表中任意圈出4个日期。观察框中的4个数，你有什么发现？请想办法记录下来。

学生动手圈、画、记录发现的规律，教师行间巡视，收集学生的作品，按序展示，引导全班仔细观察，对比交流。

先依次出示观察一组数框（圈一组的情况）、观察多组数框（圈多组的情况）。

师：在研究数组发现时，有同学只圈出了一组数，而有的同学圈出了多组数。哪种好？

生：圈多组数。

师：为什么要观察多组数？只关注一组行不行？

生：观察多组数，才能发现他们之间共同的特点。

师：这张日历中有很多这样的数，我们不仅关注一组数之间的关系，还要关注每组数中都存在的共性关系。

展示不同的学生作品，呈现不同的记录表达方式。

生1用文字语言表记录：（圈出两组数：“11、12、18、19”和“7、8、14、15”）12比11多1，19比18多1，18比11多7，19比12多7，11加19等于12加18；8比7多1，15比14多1，14比7多7，15比8多7，7加15等于8加14；横着看相邻的两数差1，竖着看相邻的两数差7，斜着看对角的两数相加的和一样多。

生2用算式表达：（圈出两组数：“11、12、18、19”和“14、15、21、22”）

12-11＝1 15-14＝1

19-18＝1 22-21＝1

18-11＝7 21-14＝7

19-12＝7 22-15＝7

11＋19＝18＋12 14＋22＝21＋15

生3、生4用符号（图形、字母）的方式表达：

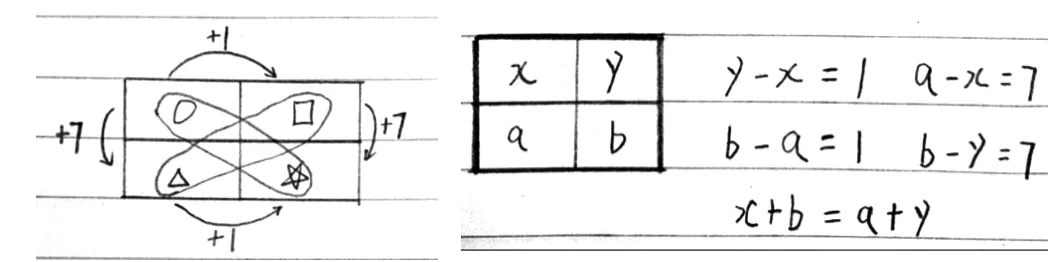
生5、生6用了不同思维层级的符号（图形、字母）方式表达：

教师引导学生对比交流（略）。

“有意栽花花自开！”在上述案例中，我借助教材中的原生态素材，适当调整教学内容，改变学习方向，挖掘延伸教材中的问题链，适当增加学生的探索和创造性的数学活动，充分发挥问题情境的价值，引导学生经历符号思考和符号表达的过程，从文字、算式表达，到图形、字母符号，感受不同数学表达方式的特点，在评价中不断缺憾，不断完善，让学生感受集简练性、概况性于一体的数学符号表征方式的精彩之处，体会符号思考的数学价值，进而渗透和发展学生的符号意识。

笔者继续思考：符号意识的培育的核心目标是什么？笔者以为，简而言之，就是让学生心中有“符号”。心中有符号，学生才能用数学的眼光观察世界；心中有符号，才能用数学的思维思考世界；心中有符号，才能用数学的语言方式表达世界。心中有符号，还能帮助学生表达对数学世界沸腾的情感。而要让学生心中有符号，就需要我们在教学中活用教材，延伸问题链，抓住一切学习契机帮助学生在心中建立符号，感受符号思考的价值，渗透学生的符号意识。总之，无论是“无心插柳”还是“有意栽花”都告诉我：心中有符号，数学更美好！