两道数列高考题的解法探析
2018-10-08海南省海南师范大学附属中学王小莉
□海南省海南师范大学附属中学 王小莉
数列是高中数学中的一个重要内容,数列中蕴含着丰富的数学思想。其中转化思想与整体思想在求解一些数列问题时,能帮助我们较快理清解题的思路找到解题的突破口。下面结合两道高考题分析转化思想与整体思想在解决数列问题中的应用。
例1(2012年海南高考理科数学第16题)数列{an}满足an+1+(-1)nan=2n-1,则数列{an}的前60项和为____________。
分析:题目仅给出数列{an}的递推关系an+1+(-1)nan=2n-1,未给出其初始值,因此数列{an}是不确定的。若从方程的角度看,递推关系an+1+(-1)nan=2n-1中涉及两个未知an与an+1数,但只有一个方程,从而无法求出其通项公式。故解答此题时,不能往“由递推公式求通项公式再求和”这一思路探寻解法,得另寻其它解法。
观察到递推公式an+1+(-1)nan=2n-1右边为大家所熟悉的等差数列{2n-1}的通项,这自然会引发我们思考:能否把这个非等差数列求和问题转化为等差数列求和问题?如何转化?左边要想出现和式,关键是要把递推关系an+1+(-1)nan=2n-1中的变号因式(-1)n给消去,由此萌生以下想法:①由条件:an+1+(-1)nan=2n-1
②可得:an+2+(-1)n+1an+1=2n+1;
③当n=2k(k ∈N*)时,②+①得:a2k+a2k+2=8k;
④n=2k-1(k ∈N*)当时,②-①得:a2k-1+a2k+1=2.
即相邻的两个奇数项的和为常数,相邻两个偶数项的和为等差数列。因此,对于求该数列的前60项的和,可考虑分别求前60项中奇数项的和与偶数项的和,再相加可得前60项的和。解答如下:
解法1:数列{an}满足 an+1+(-1)nan=2n-1,
①所以有:an+2+(-1)n+1an+1=2n+1;
②当n=2k(k∈N*)时,②+①得:a2k+a2k+2=8k;
③当n=2k-1(k∈N*)时,②-①得:a2k-1+a2k+1=2;
④当k=1,3,5,…,29时,有
(1)a1+a3=2,a5+a7=2,a9+a11=2,…,a57+a59=2(共15个等式);
(2)a2+a4=8,a6+a8=24,a10+a12=40,…,a58+a60=232,分别把上面15个等式相加得:

以上两式相加可得数列{an}的前60项和为1830。
由解法1,容易联想到下面的解法2:
解法2:由解法1知,数列{an}满足以下关系:
a2k+a2k+2=8k(k∈N*) ③
a2k-1+a2k+1=2(k∈N*) ④
③+④得a2k-1+a2k+a2k+1+a2k+2=8k+2(k∈N*)
记Sn为数列{an}的前几项和则,S4,S8-S4,S16-S8…构成首项为10、公差为16的等差数列。故数列{an}的前60项和为
拓展:由以上解法可知,我们可求该数列的任意前4n项和S4n。
若用解法1可先分别求其前4n项中的奇数项的和S奇=2n与偶数项的和S偶=再相加可得S4n=8n2+2n。
若用解法2,则该数列的前4n项和为:S4n=10n+
评析:本题的解法,充分体现了数学中的转化思想。其转化思想体现在把非等差数列求和问题转化为等差数列求和问题。其中对等差数列通项结构特征的熟悉与敏感度是联想转化的基础。由此可以看出,等差数列与等比数列是高中阶段重点学习的两个典型数列,掌握好这两个数列对进一步研究其它一般数列有着重要意义。[1]
在解决本例时,我们将局部的问题通过适当的增减,使之成为一个完整的有联系的整体,让问题中的局部与整体的关系有机联系起来,显露出问题的本质,从而使问题的解决找到捷径。[2]这就是数学中整体思想的体现。
例2(2014海南高考理科数学第17题)已知数列{an}满足a1=1,an+1=3an+1。
分析:第(Ⅰ)小题为由递推公式求通项公式,且递推公式的结构较常规,学生不难解答。
又a1+是以为首项,3为公比的等比数列。
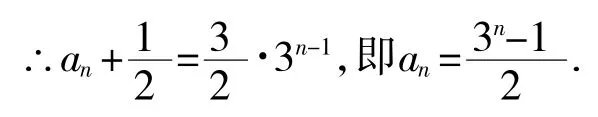
第(Ⅱ)小题是证明一个和式小于常数,常规思路是把和式的值求出来,再比较。但困难恰在此和式的求值。
第(Ⅱ)小题的本质上是一个不等式的证明,对不等式的证明,还可考虑放缩法,如何放缩呢?评分标准给出如下放缩方法:
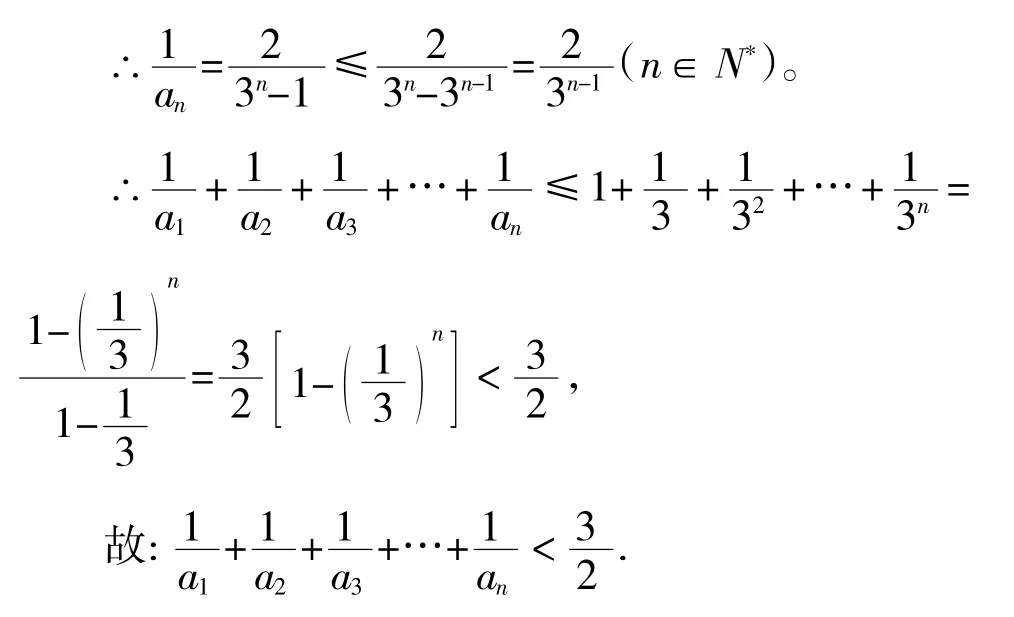
笔者认为,此题利用转化思想,把非等比数列通过放缩,转化为一个等比数列求和,思路自然,解法巧妙。但是,我们分析把放大为的过程:一种变形是还有一种变形是
这两种放缩过程,都是采取把分母缩小的方法来放大分式的值。但不管是哪一种,都是很大胆的放缩,在第一种放缩方法中,采取了原分母减去(3n-1-1),而当n→∞时,(3n-1-1)→∞;第二种放缩方法中,直接去掉分母中的多个非负项。这样的放缩方法学生一般不容易想到,也就无法采用以上方法求解此题。那是否有较常规的放缩方法呢?我们还是回到题目条件中来。
由an+1=3an+1得
由(Ⅰ)知,an=为关于n递增型指数型函数,放大分式的值,这是很符合常规的放缩方法。而要想出现所证问题中的和式,需累加,即:n →∞时,(3an+1)→∞,所以把上式中的分母缩小1以
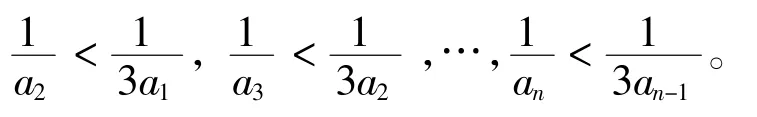
把这n-1个式子相加得:

由an+1=3an+1得,
所以有:

把这n-1个式子相加得:
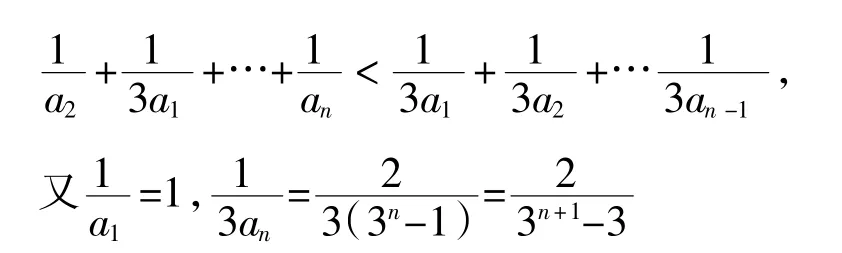
从而有:
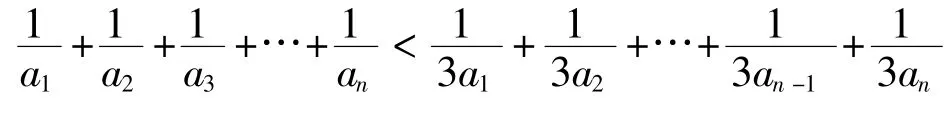
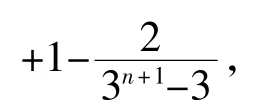

评析:此题的第(Ⅱ)小题重在考察不等式证明的放缩法。可以这么说,证法一采取了不寻常的放缩后化为寻常问题的求解;而证法二采用了寻常的放缩后,从整体观点出发,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理。[3]证法二中整体思想的应用使证题过程巧妙地避开了求和的环节,简化了证题过程,让我们感受到整体思想在解决数列问题中的巨大魅力。
