背后存在空洞时盾构隧道管片的开裂机理及承载能力分析

凌同华，张亮,2，谷淡平，刘浩然，曹峰



背后存在空洞时盾构隧道管片的开裂机理及承载能力分析

凌同华1，张亮1,2，谷淡平1，刘浩然1，曹峰1

(1. 长沙理工大学 土木与建筑学院，湖南 长沙 410114； 2. 长沙理工大学 桥梁结构安全控制湖南省工程实验室，湖南 长沙 410114)

为探讨盾构隧道管片背后存在空洞时管片空间受力特征及承载力变化情况，基于扩展有限元原理，采用载荷-结构计算方法，以长沙轨道交通2号线为研究背景，建立隧道衬砌三维计算模型，分别对衬砌结构16点位和2点位背后存在空洞时衬砌结构空间受力特征进行分析比较，根据分析结果，再对衬砌结构2点位背后存在空洞时衬砌结构极限承载力变化情况、开裂形态进行模拟分析。研究结果表明：衬砌结构16点位和2点位背后分别存在沿环向20°，30°和40°范围空洞时，空洞处衬砌应力集中明显，但均未出现开裂现象；随着荷载的增大，管片开裂主要位于管片环8点位和2点位方向，8点位处表现为内侧纵向开裂，2点位处表现外侧环向开裂；空洞的存在明显降低了衬砌结构的极限承载力，当衬砌结构2点位背后存在沿环向40°空洞时，衬砌极限承载力下降了30.68%。该研究可为隧道衬砌裂缝诱因分析、衬砌病害防治与修复研究提供一定的参考与借鉴。

盾构隧道；受力特征；承载能力；扩展有限元；空洞；管片

盾构施工法以其适用范围广、对周围环境影响小、安全高效等优势已成为地下铁道建设中的主流施工方法[1−3]。盾构隧道的支护结构主要是预制式管片衬砌，然而在盾构隧道修建过程中，受施工因素或围岩条件影响，管片背后很可能出现空洞[4]。空洞给隧道施工及运营带来极大安全隐患，开展衬砌背后空洞形式下衬砌结构受力特征及安全性的研究具有重要工程意义[5]。近年来，国内外学者在盾构隧道衬砌背后空洞研究方面做了不少富有成效的工作，并取得了诸多有价值的成果[6−11]。相关研究基本上是从应力或变形角度出发，主要分析了背后存在空洞条件下的隧道衬砌压力分布规律或定性地判断裂缝是否会产生，但并未进一步开展基于扩展有限元原理下的衬砌结构开裂状态、裂缝扩展规律及承载力变化直观性、定量化研究。同时，此类研究基本上是采用地层−结构计算模式[12−13]，与地层−结构模型相比，载荷−结构模型以衬砌结构为承压主体承受来自围岩的荷载，同时考虑围岩对衬砌结构变形的约束作用，能较为准确地反映衬砌受力的客观情况。本文以长沙轨道交通2号线一期工程为研究背景，基于扩展有限元原理和载荷−结构计算方法，采用ABAQUS软件建立盾构隧道衬砌三维计算模型，分别对衬砌结构16点位和2点位背后存在空洞时管片空间受力情况、开裂状况进行分析，在此基础上研究衬砌结构2点位背后存在空洞时管片的极限承载力、开裂形态和裂缝扩展规律，以期较为准确地得到空洞对衬砌结构的影响，并为盾构隧道衬砌病害防治与加固维修研究提供一定的理论参考。

1 衬砌裂缝扩展有限元可行性分析

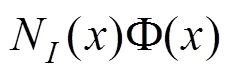
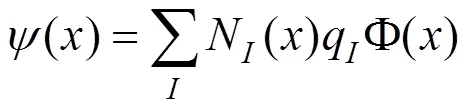
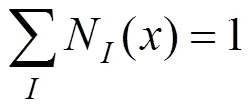
XFEM对复杂未知场(裂缝区域)的准确描述是通过在标准场近似的基础上添加扩充项实现的。结合单位分解属性式(1)，未知场u可写成：

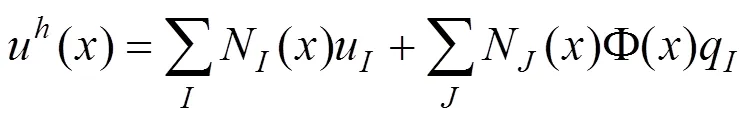
2002年，日本隧道研究所对隧道衬砌结构开展了1:1室内模型试验[18]。研究了衬砌结构顶部30°范围围岩松弛荷载、顶部空洞掉块集中力和高地压等3种工况作用下裂缝扩展情况。为了验证扩展有限元方法对衬砌结构裂损数值模拟的可行性和适用性，选择衬砌结构顶部30°范围围岩松弛荷载工况为参考案例，模拟分析在衬砌顶部30°范围内存在围岩松弛荷载作用下裂缝的产生与发展过程。数值模拟采用载荷−结构计算模型，通过设置弹簧单元来模拟围岩抗力，衬砌结构参数与文献[18]中所列试验参数一致，衬砌管片外半径为9.7 m，内径为9.4 m，厚度为0.3 m，弹性模量20.7 GPa，泊松比为0.2。采用混凝土材料。裂缝扩展采用最大主应力开裂准则。

扩展有限元数值模拟得到衬砌顶部在松弛荷载作用下，首先在顶部内侧出现张拉裂缝，随着荷载继续增加，顶部内侧裂缝不断向外侧扩展增大，在裂缝即将贯穿顶部断面时，衬砌结构14点位和2点位方向出现较大的拉应力，并且出现裂缝，最后衬砌由于顶部完全断开而失去承载力。图1分别为试验与扩展有限元方法分析得到的衬砌结构裂缝分布图，通过分析对比，可知在裂缝产生的位置和时间先后顺序上，两者基本吻合。因此，采用扩展有限元方法来模拟衬砌结构开裂及裂缝扩展规律是适用的。

日本隧道所试验-Mashimo：

XFEM数值模拟结果：

图1 试验与扩展有限元模拟结构破坏裂缝对比图

Fig. 1 Cracks comparison of structural damage between test and XFEM simulation

2 工程概况

长沙轨道交通2号线一期工程整体为东西走向，线路正线长21.923 km，均为地下线，设站19座，均为地下站。主要采用盾构法开挖掘进，盾构隧道设计为双线单孔隧道，隧道内径为5 400 mm，采用圆形预制钢筋砼管片衬砌。

长沙轨道交通2号线勘察区内上覆土层主要为人工填土、细砂、砾石，揭露基岩为白垩系泥质粉砂岩(粉砂质砾岩)。根据岩体的风化程度可分为：全风化带、强风化带和中风化带。地铁隧道穿越地层主要为强风化泥质粉砂岩和中风化泥质粉砂岩，强风化泥质粉砂岩围岩等级为Ⅴ级，中风化泥质粉砂岩围岩等级为Ⅳ级。区内广泛分布的白垩系泥质粉砂岩(砾岩)强风化～中风化层，具遇水软化、失水易干裂的特点。

3 衬砌结构扩展有限元分析与计算

3.1 模型建立

盾构隧道管片环外径为6 000 mm，内径为 5 400 mm，厚度为300 mm，管片环宽1 500 mm，拼装方式为错缝拼装，错缝角度为45°，每环由6块管片构成。盾构隧道衬砌结构三维模型见图2。整环衬砌由3环管片组成，将中间环作为主要分析对象，前后2环为错缝拼装受力结构和中间环的边界条件，不作为计算分析对象[19]。

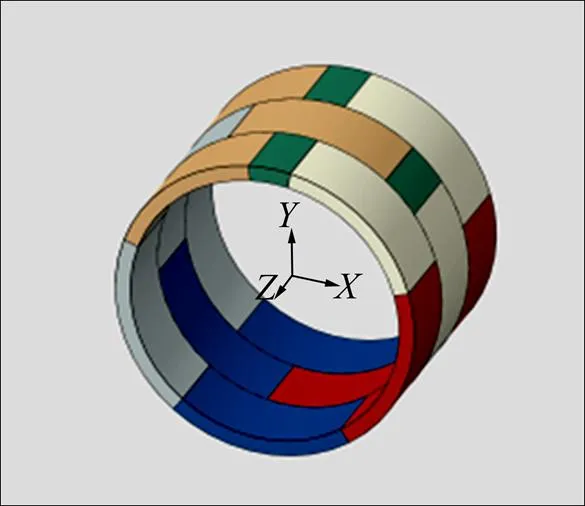
图2 盾构隧道衬砌结构三维模型

在管片结构与地层间的相互作用方面，因主要考虑并分析衬砌的受力状态，采用载荷−结构分析方法，以衬砌结构为承压主体承受来自围岩施加的荷载，并考虑围岩对衬砌结构变形的约束作用。具体实现方法为：在管片外表面均匀设置弹簧单元，弹簧的一端和衬砌外圆弧面建立耦合，另一端采用完全固定边界。施加弹簧约束后的衬砌结构三维模型如图3所示。

图3 施加弹簧约束的衬砌结构三维模型

3.2 计算参数

管片采用C50混凝土，围岩弹性抗力系数取200 MPa/m[20]。裂缝扩展采用最大主应力开裂准则，混凝土抗拉强度f=1.89 MPa，断裂能Ⅰ=Ⅱ=Ⅲ=150 N/m。其余相关材料参数见表1。

当代不同形式的艺术似乎都有试图消解与观众之间距离的倾向，公共艺术在这方面和其他艺术形式相比更具优势，公共艺术因其”公共性”的特征，决定了比其他艺术形式更具“开放性”。这种“开放性”一方面体现在创作开始阶段就要考虑设计出大众可以充分互动的作品，使艺术与公众发生直接的关联；另一方面还可能让公众成为艺术创作的参与者和艺术家一起完成公共艺术实践。公共艺术方案的确定、实施过程以及最终结果，可以让大众充分参与，大众和艺术家一起成为创作主体，展现自己的艺术潜质，获得创造与表达的快乐。这样就使艺术与公众始终处于共存互动之中，最终呈现出丰富、包容的艺术形态。

表1 预制管片材料参数

3.3 空洞影响下管片开裂分析

长沙地铁盾构隧道埋深为=20 m，土层容重=19.6 kN/m3，侧向土压系数为0.53，结合太沙基松弛土压力理论[21−22]，可得管片环顶部的上覆水土荷载1=235.2 kPa，隧道基底反力2=278.75 kPa，管片环顶部的侧向水土压力3=124.656 kPa，管片环底部的侧向水土压力4=186.984 kPa。

表2 管片结构背后空洞模拟计算工况

3.3.1 空洞作用下管片开裂模拟

衬砌背后空洞多位于衬砌环16点位和2点位或14点位方向。将空洞设置在管片环16点位和2点位方向，针对2种不同的空洞位置，分2种情况进行建模分析，计算3种空洞范围分别为沿环向20°，30°和40°()共6个工况条件下管片空间受力情况及开裂状况，计算工况如表2所示。采用地层弹簧缺失和外荷载缺失的方式模拟空洞，无弹簧及施加外荷载的位置和范围即空洞所在位置。盾构隧道管片点位和衬砌结构背后空洞计算模型示意图如图4和图5所示。图6为工况1计算模型。2图中弹簧缺失的位置和范围即空洞所在位置。

图4 盾构隧道管片点位示意图

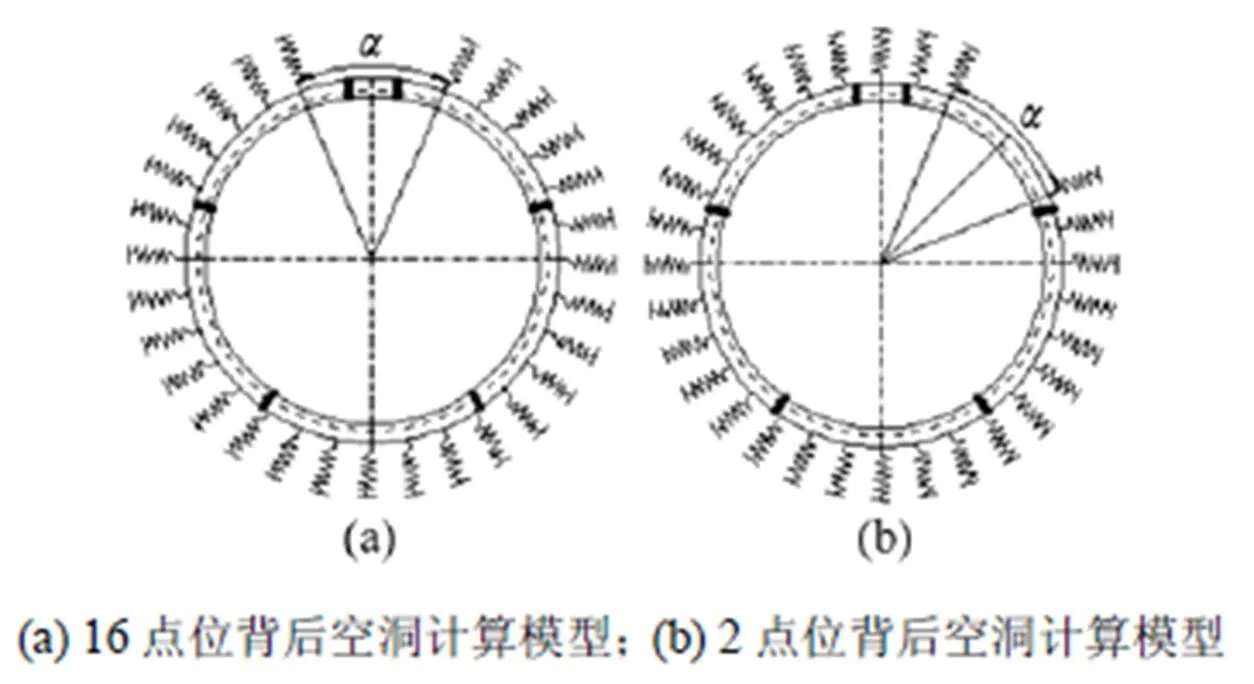
图5 衬砌背后空洞计算模型示意图

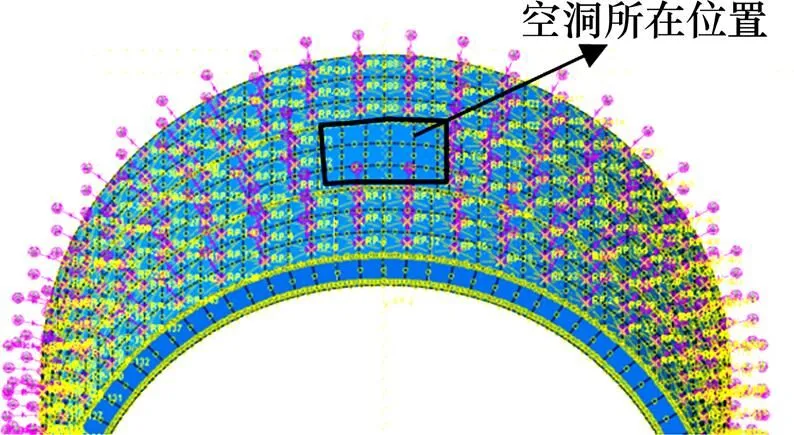
图6 工况1计算模型

图7为管片环16点位背后分别存在沿环向20°，30°和40°范围空洞时衬砌结构的最大主应力等值线图。

从图7可知，管片空洞缺陷处应力集中非常明显，最大主应力值均位于空洞的中心位置，空洞处管片处于受拉状态；而空洞之外区域最大主应力均匀分布，管片均处于受压状态。空洞的存在极大地改变了管片的应力分布。当空洞范围为20°时，空洞处管片最大主应力值为5.377×105Pa，空洞范围为30°时，管片最大主应力值为9.699×105Pa，空洞范围增大到40°时，空洞处管片最大主应力值为1.128×106Pa，缺陷处管片最大主拉应力值随空洞范围的增大而增大。管片极限开裂强度f=1.89 MPa，3种工况下管片的最大主拉应力均未超过管片开裂强度，从图中也可看出管片未出现开裂现象。

管片环2点位背后分别存在沿环向20°，30°和40°范围空洞时衬砌最大主应力情况见图8。

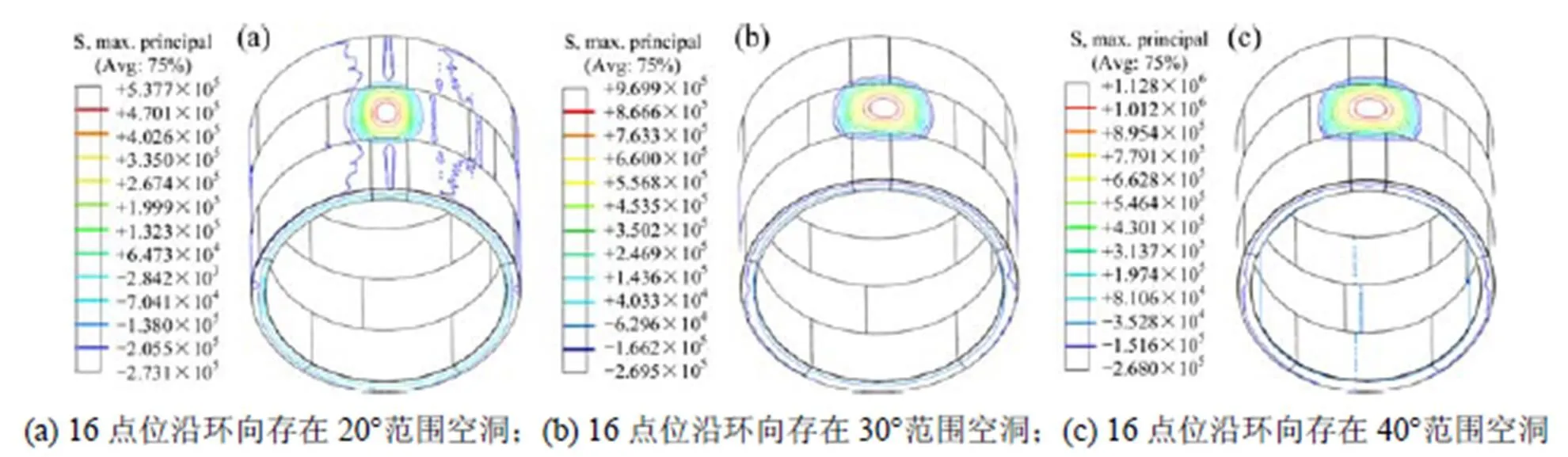
图7 管片环16点位背后存在空洞时管片最大主应力等值线图

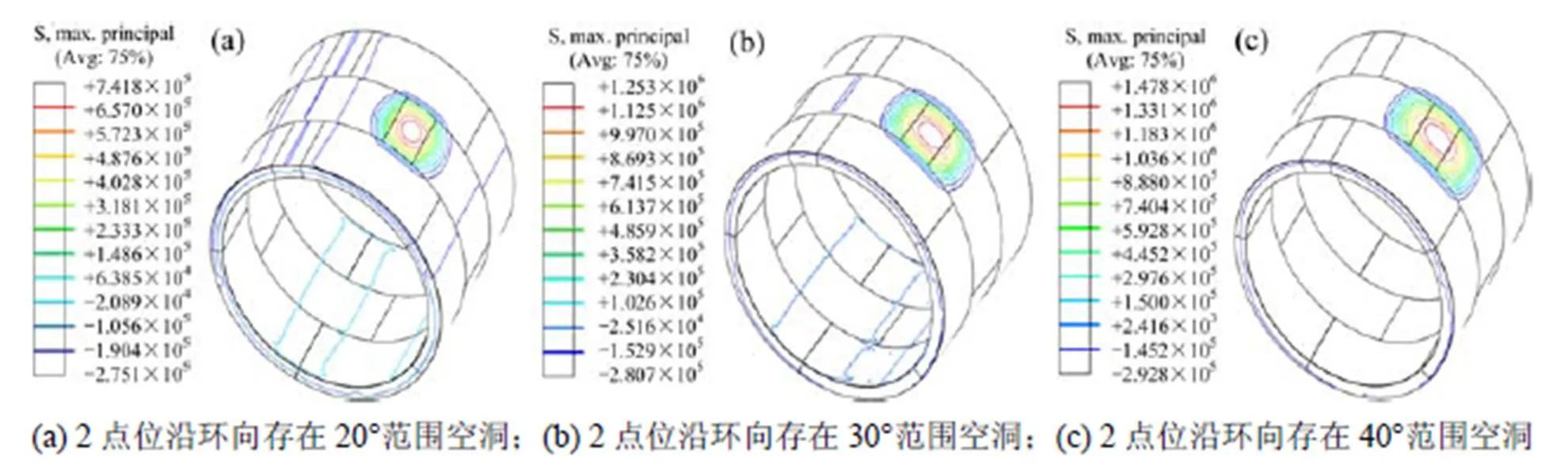
图8 管片环2点位背后存在空洞时管片最大主应力等值线图

由图8可看出，管片环2点位背后空洞的存在很大程度地影响了管片的应力分布。拱肩空洞处衬砌应力集中明显，应力集中区域随空洞范围的增大而增大，空洞处管片表现为受拉状态，最大主拉应力值均位于空洞中心位置，且随着空洞范围增大而增大，当空洞范围为沿环向40°时，最大主拉应力值为1.478 MPa，未超过管片开裂强度，从图中可知管片未发生开裂。

3.3.2 结果分析与对比

管片环16点位和2点位背后分别存在相同范围空洞时管片最大主应力值对比见图9。由图9可知，2种不同位置空洞影响下管片最大主应力值均随空洞范围的增大而增大，但最大主应力值均未达到管片开裂强度，即管片未出现开裂现象。从图9也可看出，在同样空洞大小范围情况下，管片环2点位背后存在空洞条件下管片产生的最大主拉应力值总是大于拱顶存在空洞情况，2点位背后存在空洞情况下，管片最大主拉应力值更接近管片极限抗拉强度，即相对16点位背后存在空洞情况，当管片环2点位背后存在相同大小范围空洞缺陷时管片更不稳定，更易发生开裂。

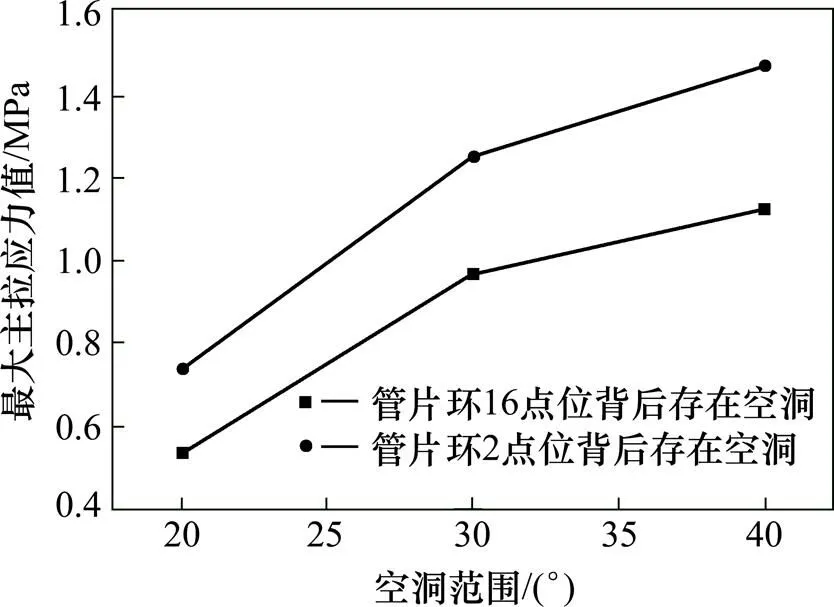
图9 管片环16点位和2点位背后分别存在空洞情况下管片最大主应力对比图

4 背后空洞影响下衬砌结构承载力分析

与管片环16点位背后存在空洞相比，当2点位背后存在相同大小范围空洞时，空洞对衬砌应力分布、安全性的影响更大。考虑空洞对衬砌结构整体安全性影响较大的情况，以使计算及工程实践偏于保守，在此，针对管片环2点位背后存在一定范围空洞影响的衬砌结构，采用ABAQUS软件进行极限承载力分析和开裂特征分析。

将模型分析时因大变形而造成的迭代不收敛前的荷载值作为管片结构的极限荷载。完整围岩条件下与衬砌背后存在空洞条件下管片极限承载力及极限承载力变化情况见表3。从表3可看出，随着衬砌结构2点位背后空洞范围的增大，管片极限承载力减小，当空洞范围增大至沿环向40°时，管片极限承载力仅为427 kPa，下降了30.68%。

表3 完整围岩条件与背后存在空洞条件管片极限承载力情况

图10反映的是无空洞时与管片环2点位背后沿环向分别存在20°，30°和40°范围空洞时衬砌结构在极限承载力情况下的开裂形态及最大主应力图。

(a) 管片背后无空洞；(b) 管片环2点位背后沿环向存在20°范围空洞；(c) 管片环2点位背后沿环向存在30°范围空洞；(d) 管片环2点位背后沿环向存在40°范围空洞

当管片处于完整围岩条件下时，极限承载力情况下仰拱出现沿管片走向的纵向裂缝，裂缝位于管片内侧，主裂缝长度为0.85 m，深度为105 mm；当衬砌2点位背后出现沿环向20°范围空洞缺陷时，极限承载力情况下管片环8点位内侧出现纵向裂缝，主裂缝长0.22 m，深107 mm；当衬砌结构2点位背后沿环向分别出现30°和40°范围空洞时，极限承载力情况下均在管片环2点位方向外侧空洞缺陷处出现环向裂缝，主裂缝长分别为1.12 m和1.44 m，深度分别为110 mm和111.5 mm。空洞缺陷处管片开裂扩展规律均为：随着加载步的进行，首先在管片环2点位方向处出现1条环向主裂缝，紧接着沿管片走向生成若干条对称于主裂缝的环向 裂缝。

5 结论

1) 长沙地铁盾构隧道埋深20 m以内，当隧道衬砌结构16点位或2点位背后分别存在沿环向20°，30°和40°空洞时，空洞处衬砌应力集中非常明显，但均未出现开裂现象，最大主拉应力值随空洞范围的增大而增大。

2) 与完整围岩条件下管片极限承载力相比，衬砌结构2点位背后分别存在沿环向20°，30°和40°范围空洞影响时，衬砌结构极限承载力分别为583，520和427 kPa，分别下降了5.36%，15.58%和30.68%，空洞的存在降低了衬砌结构的极限承 载力。

3) 极限承载力情况下，管片开裂主要位于管片环8点位和2点位方向，8点位处分布纵向裂缝，2点位处基本为环向裂缝。

[1] 王梦恕. 中国盾构和掘进机隧道技术现状、存在的问题及发展思路[J]. 隧道建设, 2014, 34(3): 179−187.WANG Mengshu. Tunneling by TBM/shield in China: state-of-art, problems and proposals[J]. Tunnel Construction, 2014, 34(3): 179−187.

[2] 何川, 封坤, 方勇. 盾构法修建地铁隧道的技术现状与展望[J]. 西南交通大学学报, 2015, 50(1): 97−109.HE Chuan, FENG Kun, FANG Yong. Review and prospects on constructing technologies of metro tunnels using shield tunnelling method[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 97−109.

[3] 黄阜, 李在蓝, 朱亮, 等. 基于自定义本构模型的盾构隧道开挖面极限支护力研究[J]. 铁道科学与工程学报, 2016, 13(5): 891−897.HUANG Fu, LI Zailan, ZHU Liang, et al. The study of ultimate support pressure of shield tunnel face subjected to user-defined constitutive model[J]. Journal of Railway Science and Engineering, 2016, 13(5): 891−897.

[4] 方勇, 郭建宁, 康海波, 等. 富水地层公路隧道衬砌背后空洞对结构受力的影响[J]. 岩石力学与工程学报, 2016, 35(8): 1648−1658.FANG Yong, GUO Jianning, KANG Haibo, et al. Influence of voids behind lining on the mechanical behavior of lining structure of highway tunnel in watery strata[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(8): 1648−1658.

[5] 张顶立, 张素磊, 房倩, 等. 铁路运营隧道衬砌背后接触状态及其分析[J]. 岩石力学与工程学报, 2013, 32(2): 217−224.ZHANG Dingli, ZHANG Sulei, FANG Qian, et al. Study of contact state behind tunnel lining in process of railway operation and its analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 217−224.

[6] 刘永华. 二次衬砌结构拱顶存在空洞或裂缝的数值模拟[J]. 公路隧道, 2006(3): 11−13.LIU Yonghua. Numerical simulation of the existence of voids or cracks in the vault of secondary lining structure[J]. Highway Tunnel, 2006(3): 11−13.

[7] 曲荣怀. 衬砌背后空洞对隧道围岩压力分布规律的影响研究[D]. 北京: 北京交通大学, 2014.QU Ronghuai. Study on the influence laws of voids behind lining on the distribution of tunnel surrounding rock pressure[D]. Beijing: Beijing Jiaotong University, 2014.

[8] Meguid M A, Dang H K. The effect of erosion voids on existing tunnel linings[J]. Tunnelling & Underground Space Technology, 2009, 24(3): 278−286.

[9] 王亚琼, 刘占良, 张素磊, 等. 在役公路隧道素混凝土衬砌裂缝稳定性分析[J]. 中国公路学报, 2015, 28(7): 77−85.WANG Yaqiong, LIU Zhanliang, ZHANG Sulei, et al. A fracture mechanics-based approach for crack stability analysis of liner in highway tunnel[J]. China Journal of Highway and Transport, 2015, 28(7): 77−85.

[10] 罗勇. 隧道衬砌开裂机理及控制方法研究[D].成都:西南交通大学, 2010.LUO Yong. Study on the mechanism of crack generation and control methods of tunnel lining[D]. Chengdu: Southwest Jiaotong University, 2010.

[11] 周强.高速公路隧道衬砌背后空洞影响及安全性分析[D]. 重庆:重庆交通大学, 2013.ZHOU Qiang. Effects and safety analysis of caverns behind highway tunnel lining[D]. Chongqing: Chongqing Jiaotong University, 2013.

[12] 冯岗. 隧道衬砌厚度不足和背后空洞对衬砌结构安全性影响研究[D]. 北京: 北京交通大学, 2013.FENG Gang. A study on the structure security of lining--based on the influences of insufficient lining thickness and the voids existing at the back of lining[D]. Beijing: Beijing Jiaotong University, 2013.

[13] 雷波, 漆泰岳, 陈小雨, 等. 背后空洞引起高速铁路隧道衬砌裂缝形态的FEM对比分析[J]. 铁道标准设计, 2015(9): 104−108.LEI Bo, QI Taiyue, CHEN Xiaoyu, et al. FEM-based contrastive analysis of lining cracks caused by cavity behind arch shoulder in high-speed railway tunnels[J]. Railway Standard Design, 2015(9): 104−108.

[14] 张晓东, 丁勇, 任旭春.混凝土裂纹扩展过程模拟的扩展有限元法研究[J]. 工程力学, 2013, 30(7): 14−21.ZHANG Xiaodong, DING Yong, REN Xuchun. Simulation of the concrete crack propagation process with the extended finite element method[J]. Engineering Mechanics, 2013, 30(7): 14−21.

[15] Fleming M, Chu Y A, Moran B, et al. Enriched element-free galerkin methods for crack tip fields[J]. International Journal for Numerical Methods in Engineering, 1997, 40(8): 1483−1504.

[16] Stazi F L, Budyn E, Chessa J, et al. An extended finite element method with higher-order elements for curved cracks[J]. Computational Mechanics, 2003, 31(1): 38−48.

[17] Melenk J M, Babuška I. The partition of unity finite element method: Basic theory and applications[J]. Computer Methods in Applied Mechanics & Engineering, 1996, 139(1/4): 289−314.

[18] Mashimo H, Isago N, Yoshinaga S, et al. Experimental investigation on load-carrying capacity of concrete tunnel lining[C]// Proceedings of Twenty Eighth ITA General Assembly and World Tunnel Congress, 2002.

[19] 郭瑞, 何川. 盾构隧道管片衬砌结构稳定性研究[J]. 中国公路学报, 2015, 28(6): 74−81.GUO Rui, HE Chuan. Study on stability of segment lining structure for shield tunnel[J]. China Journal of Highway and Transport, 2015, 28(6): 74−81.

[20] 重庆交通科研设计院. 公路隧道设计规范[M].北京:人民交通出版社, 2004.Chongqing Communications Research and Design Institute. Code for design of road tunnel[M]. Beijing: China Communications Press, 2004.

[21] 段锋. 盾构地铁管片衬砌结构施工阶段力学行为及选型技术研究[D].淮南: 安徽理工大学, 2012.DUAN Feng. Study on mechanical behaviour and selection technology of segment lining structure of shield subway in construction stage[D]. Huainan: Anhui University of Science & Technology, 2012.

[22] 金浩. 浅覆土对水下盾构隧道管片上浮影响及损伤诊断技术研究[D].长沙: 中南大学, 2014.JIN Hao. Influence of shallow covering soil on underwater shield tunnel’s segment floating up and research of damage diagnosis technique[D]. Changsha: Central South University, 2014.

(编辑 蒋学东)

Analysis of cracking mechanism and bearing capacity of shield tunnel segment with voids behind

LING Tonghua1, ZHANG Liang1, 2, GU Danping1, LIU Haoran1, CAO Feng1

(1. School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha 410114, China; 2. Hunan Province Engineering Laboratory of Bridge Structure, Changsha University of Science & Technology, Changsha 410114, China)

To explore the spatial mechanical characteristics and bearing capacity change of shield tunnel segments where voids exist behind the back, based on the theory of extended finite element and by the method of load structure, the Changsha No.2 Metro Line was taken as the research example. A three-dimensional model of lining was established and the spatial stress values of lining were analyzed and compared when voids existed behind the back of the 16th point position and the second point position of lining. According to the analysis results, the ultimate bearing capacity change and the fracture morphology of lining were simulated and studied given the existence of voids behind the second point position. The results demonstrate that when the 16th point position and the second point position of lining exist voids in a range of 20°, 30° and 40°, the stress of lining is concentrated at locations near to the voids, but there is no cracking phenomenon. With the increase of load, the cracks were mainly located at the 8th point position and the second point position of the lining, whereas the 8th point position distributed medial longitudinal cracks and the cracks in the second point position were lateral and transverse. The existence of voids reduces the ultimate bearing capacity of the lining. When the second point position of the lining possesses voids in a range of 40°, the ultimate bearing capacity is decreased by 30.68%. The research study can provide a certain reference for the analysis of crack inducement of lining and the study of prevention and repair of lining distresses.

shield tunnel; mechanical characteristic; bearing capacity; extended finite element; void; segment

10.19713/j.cnki.43−1423/u.2018.09.016

U451.4

A

1672 − 7029(2018)09 − 2293 − 08

2017−06−24

国家自然科学基金资助项目(51678071, 51308072)；长沙理工大学桥梁结构安全控制湖南省工程实验室开放基金资助项目(16BCX13)；长沙理工大学研究生科院创新资助项目(CX2017BX03)

凌同华(1968−)，男，湖南双峰人，教授，博士，从事隧道与地下工程研究；E−mail：lingtonghua@163.com