界面缺陷钢管混凝土轴压极限承载力理论推导

卢进，秦鹏



界面缺陷钢管混凝土轴压极限承载力理论推导

卢进，秦鹏

(湖南大学 土木工程学院，湖南 长沙 410082)

基于核心混凝土界面缺陷对钢管混凝土构件力学性能的影响是当前研究的热点问题，钢管混凝土存在缺陷后其极限承载力会下降，且缺陷越大其承载力下降越多，但是，并没有一个定量的表达式能计算具体缺陷后的承载力。用极限平衡法对界面缺陷钢管混凝土极限承载力进行理论推导，建立3种常见界面缺陷钢管混凝土轴压短柱极限承载力近似计算公式。结合已有研究文献进行实例验证。研究结果表明用本文推导的承载力与文献试验值的折减基本趋势一致，验证了本文理论推导的可行性及精确性。

界面缺陷；钢管混凝土；极限平衡方法；承载力近似计算

由于钢管混凝土具有承载能力高，抗震性能突出，自重轻，施工方便，造价经济等优点，目前已在工程结构中得到了广泛的应用[1−3]。大量工程实践显示，实际运行过程中，伴随着力、热等荷载耦合因素作用下，钢管混凝土存在界面缺陷现象。近年来，有不少学者在界面缺陷产生的原因和界面缺陷分类以及界面缺陷对钢管混凝土受力性能的影响进行了研究，并取得了一些成果[4−9]。但是，并没有一个定量的表达式能计算具体界面缺陷后的承载力。所以本文工作是对界面缺陷钢管混凝土极限承载力进行理论推导。结构极限承载能力的计算，可以用2种不同的方法进行[2]。一种是全过程分析法，它需跟随结构的荷载历程，从结构的弹性状态开始，经过弹塑性阶段，最后到达极限状态。这种方法需知道结构材料的本构关系，但是由于界面缺陷钢管混凝土轴压过程的受力不确定和复杂性，且核心混凝土和钢材的本构模型均无法准确获得，采用全过程分析法求解有一定的难度。另一种方法是极限平衡法，它不管加载历程和变形过程，直接根据结构处于极限状态时的平衡条件算出极限状态的荷载数值。对于存在界面缺陷的钢管混凝土达到极限承载力时，混凝土和钢管的极限状态平衡条件是可知的，因此可以采用极限平衡理论。对求解界面缺陷钢管混凝土轴压短柱极限承载能力进行理论分析，建立界面缺陷钢管混凝土轴压短柱承载力的近似计算公式，为后续相关理论研究提供一种科学方法和手段。

1 基本假定

由于存在界面缺陷的钢管混凝土轴心受压短柱的变形很复杂，所以为了推导缺陷下的极限承载力近似计算公式，除了蔡绍怀《现代钢管混凝土结构》书中已有的假定，为了简化计算，还需要进行本文的基本假定：

1) 设定钢管和核心混凝土缺陷侧以及缺陷对测的应力，则中间段钢管和核心混凝土抗压强度线性变化；

2) 在缺陷下侧压力是不均匀的，但是为了简化计算，假定用最大侧压力均匀计算；

3) 三向受压混凝土的侧压系数过去一般取值3~6，侧压系数的取值考虑的因素比较多，为了简化本文中侧压系数取=3[2]；

4) 在计算中，忽略了极限状态下缺陷处钢管与混凝土的接触使得承载力的提高。因为等到接触后钢管已经产生了很大的位移，在实际工程中是不允许的，所以本文所求的承载力是未发生大幅度屈曲的情况下；

6) 适用条件：普通混凝土和不发生大幅度的屈曲；

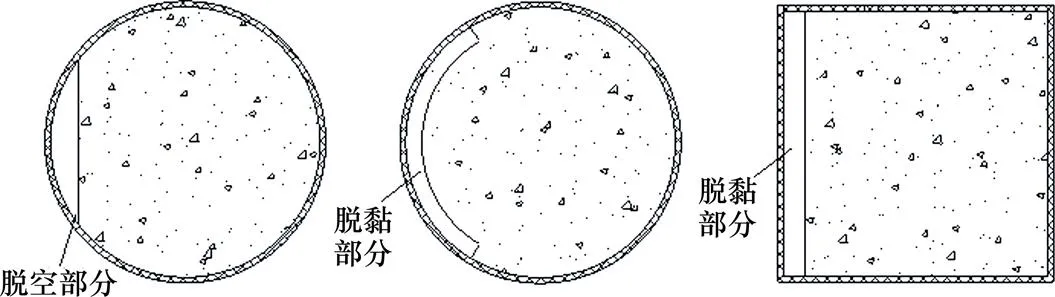
图1 3种常见界面缺陷钢管混凝土横截面图

2 脱空圆钢管混凝土承载力计算公式

因核心混凝土不服从正交流动法则，属假塑性元件，故用静力法求解。本次推导共有7个未知量，即外荷载，混凝土的纵向应力c1，钢管的纵向应力s1，s2和环向应力t1，t2，以及钢管和混凝土接触面之间的侧压力。需要建立7个独立方程才能求解[2]。

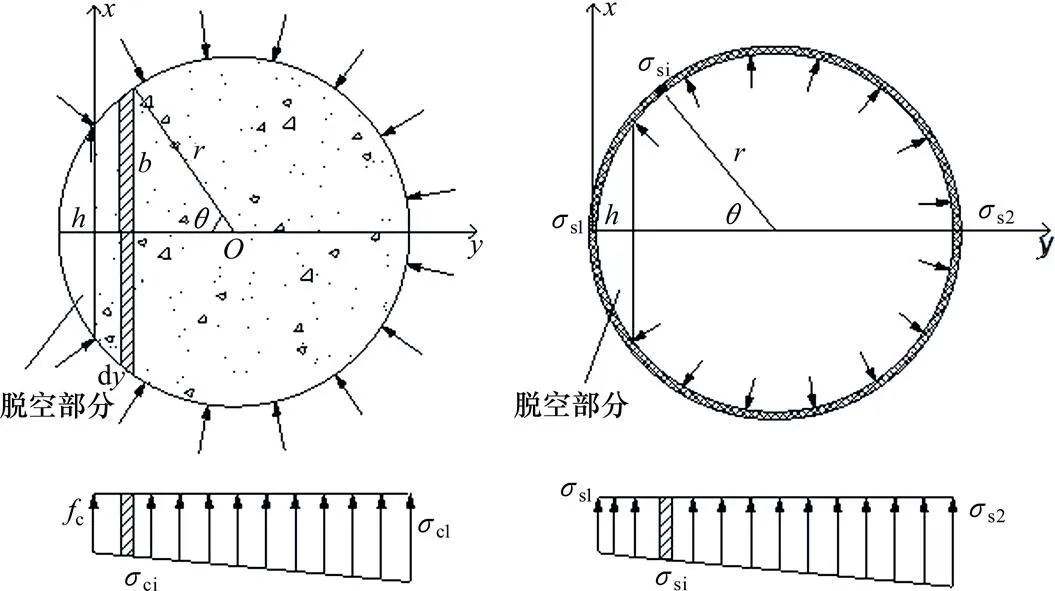
图2 核心混凝土和钢管计算简图

2.1 纵向静力平衡方程

钢管混凝土极限承载力为核心混凝土极限承载力1和考虑套箍作用的钢管极限承载力2之和：

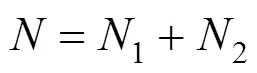
混凝土承载力1：

为简化计算，假定中间混凝土抗压强度线性变化，由几何关系可知：

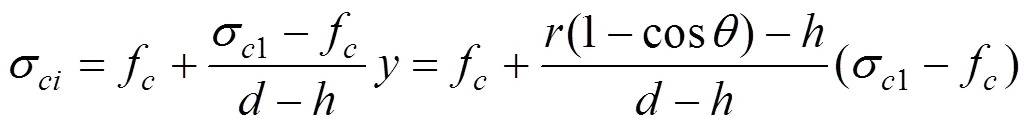
则有：

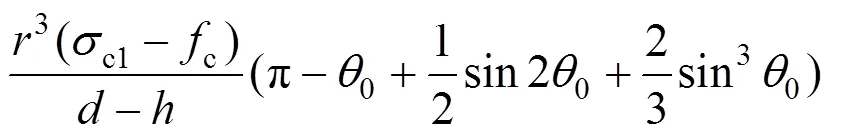
钢管承载力2：

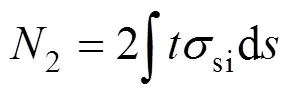
为简化计算，假定中间钢管受压强度线性变化，由几何关系可知：

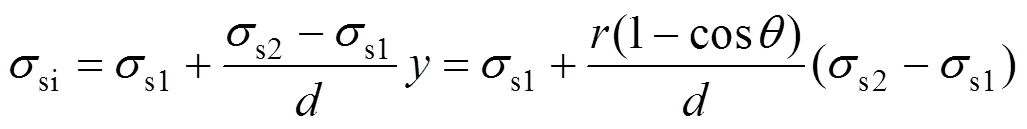
则有：

将式(3)和式(5)代入式(1)有：

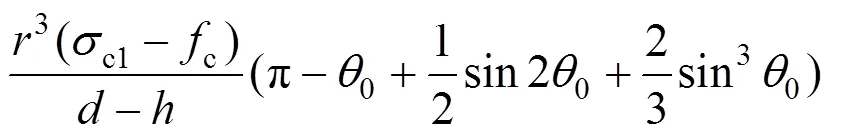
2.2 纵向弯矩平衡方程

由静力平衡条件，建立纵向弯矩平衡条件：

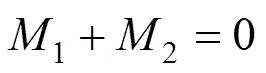
核心混凝土对中心轴的弯矩1：

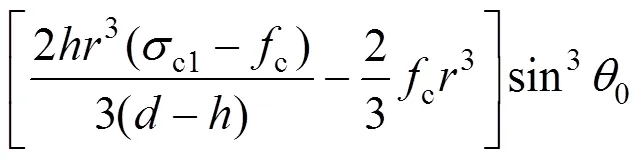
钢管对中心轴的弯矩2：

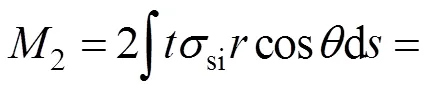
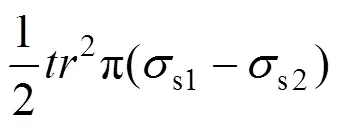
将式(8)和式(9)代入(7)有：

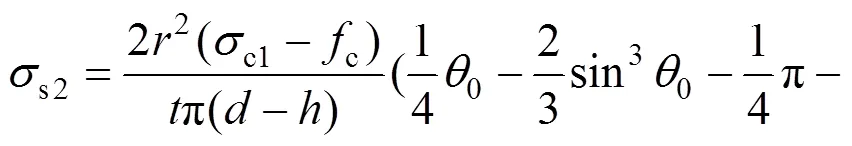
(10)

将式(10)代入式(6)且对公式进行优化可以得到脱空圆钢管混凝土极限承载力公式：

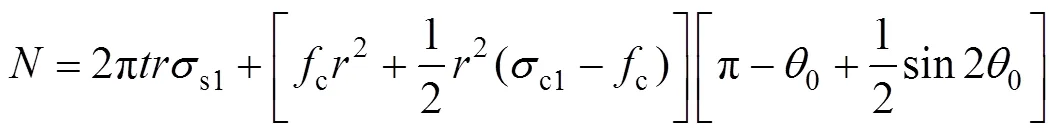
2.3 环向弯矩平衡方程

2.4 环向静力平衡方程

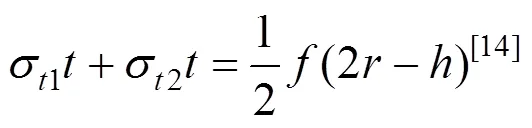
为简化用最大侧压力均匀计算，即=

2.5 脱空钢管混凝土核心混凝土三向受力方程

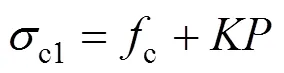
2.6 钢管屈服条件

当钢管达到屈服而开始塑流后，钢管混凝土的应变发展加剧，外观体积也因核心混凝土微裂发展而急剧增长。此时钢管处于纵压−环拉的双向应力状态(径向压力较小，忽略不计)，纵向应力为s1，环向应力为1，按照Von Mises屈服条件的规律：

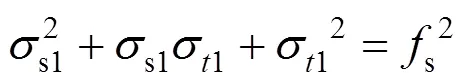
由二次求根公式得：

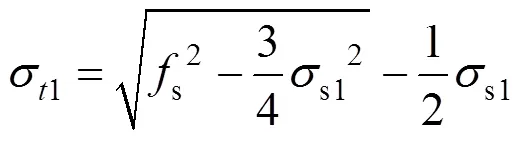
将式(17)代入式(13)有：

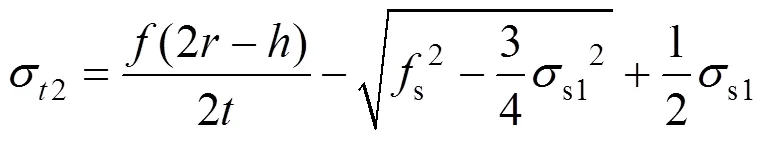
将式(17)和式(18)代入式(14)得：

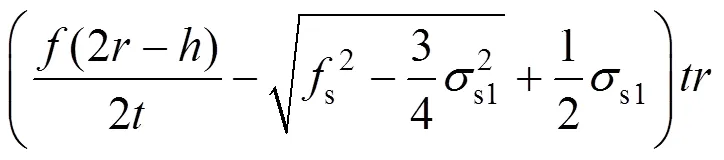
化简得：

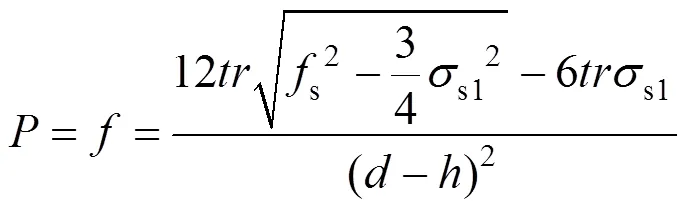
故：

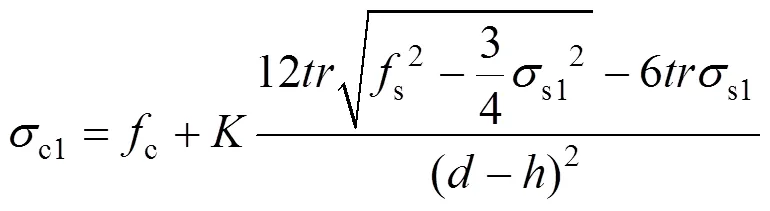
将式(20)等式两边同时对s1求导数有：

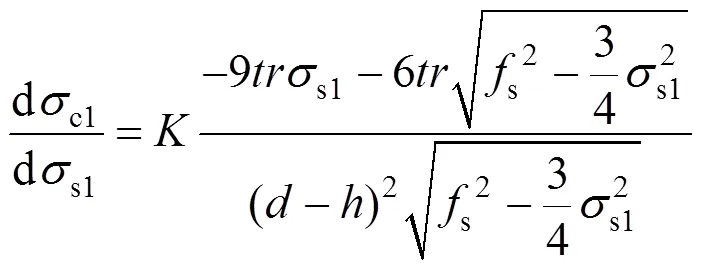
2.7 求解极值

由式(11)可见，荷载是钢管纵向应力s1的函数。我们的目标是求最大荷载max，于是将式(11)优化前的公式对s1取导数求未知量，并由极值 条件：

将式(21)代入式(22)有：

令：

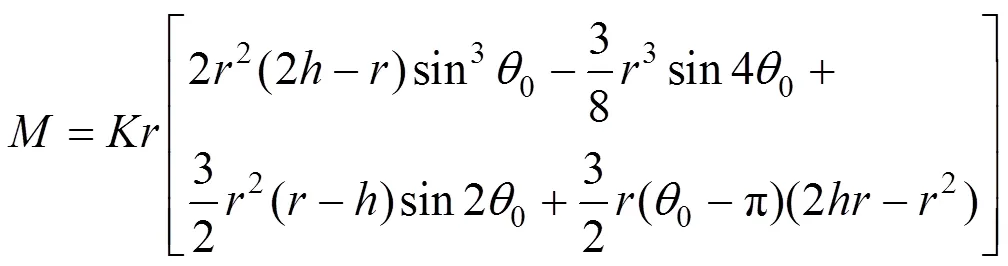
求解方程得：

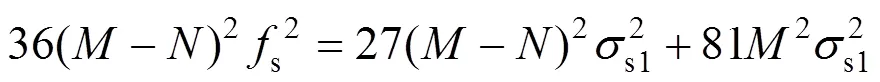
即

(23)

将式(23)代入式(11)即可得到优化后的脱空圆钢管混凝土极限承载力公式：

3 脱黏圆钢管混凝土承载力计算公式

脱黏圆钢管混凝土的推导方法与脱空类似，只是核心混凝土计算方程式存在差别，所以这一部分只列举存在差异的部分，其余的计算式都和脱空钢管混凝土相同；

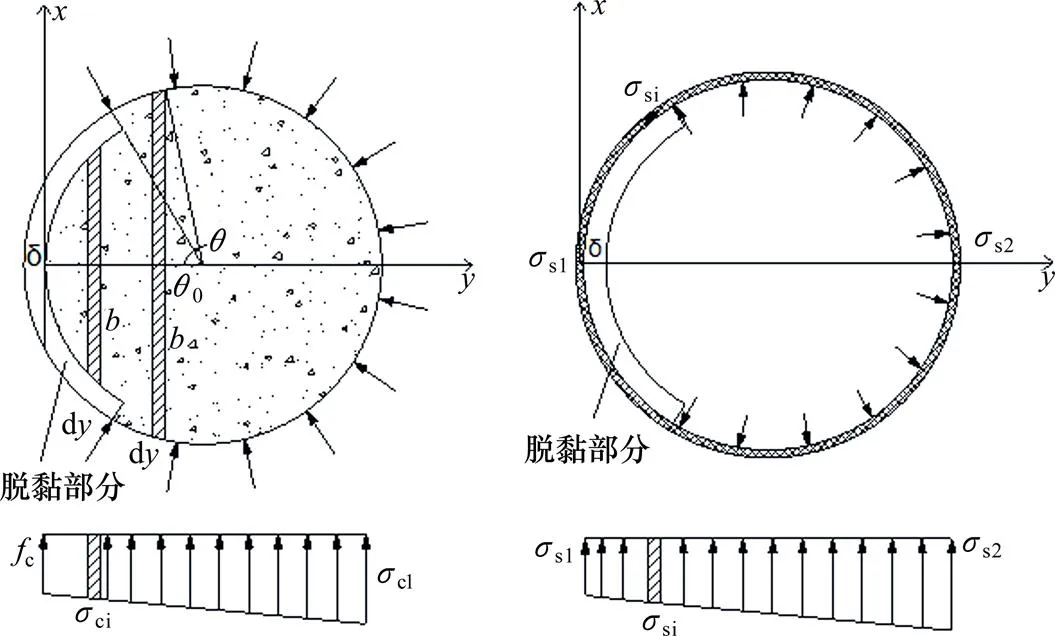
图4 核心混凝土和钢管计算简图

3.1 纵向静力平衡方程

混凝土承载力1：

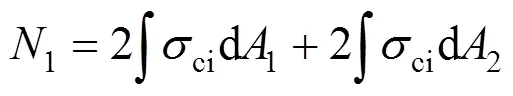
为简化计算，假定中间混凝土抗压强度线性变化，由几何关系可知：

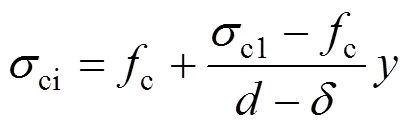
则有：

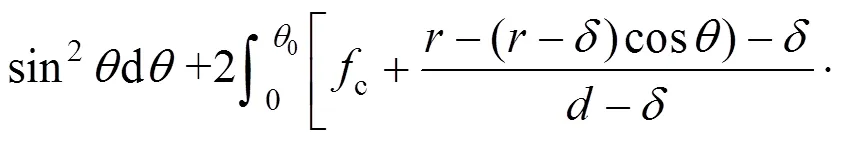
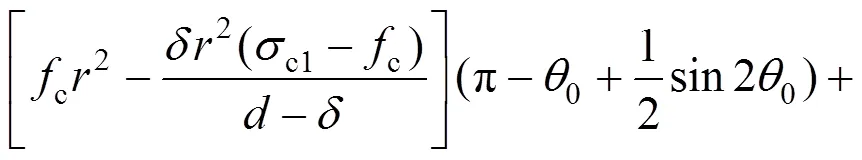
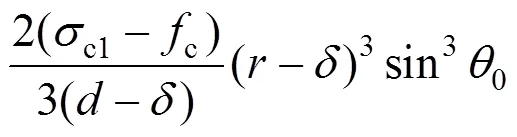
故由式(5)和式(25)可得：

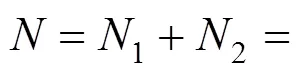
3.2 纵向弯矩平衡方程

核心混凝土对中心轴的弯矩1：

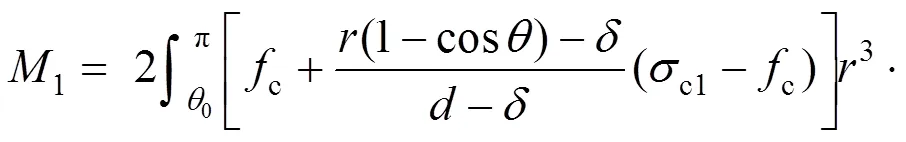
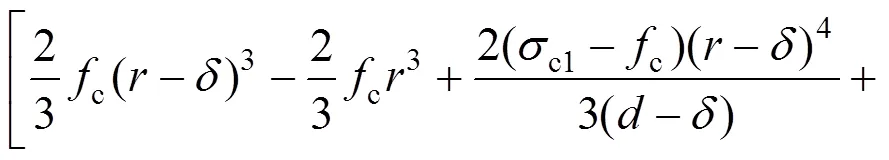
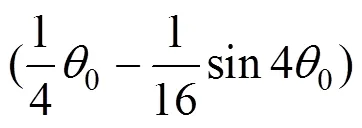
故由式(7)，(9)，(27)，(25)和(25)可以得到优化后的脱黏圆钢管混凝土极限承载力公式：

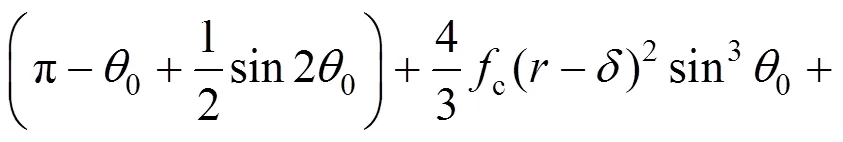
3.3 脱黏圆钢管混凝土核心混凝土三向受力方程

此部分的计算简图和脱空圆钢管混凝土的计算简图是类似，只需改变缺陷值−；所有此部分的过程省略，直接引用脱空圆钢管混凝土的结果；

3.4 求解极值

由式(28)可见，荷载是钢管纵向应力s1的函数。我们的目标是求最大荷载max，于是将式(28)优化前的公式对s1取导数，并由极值条件求解 方程：

令：

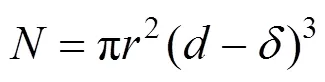
求解方程得：

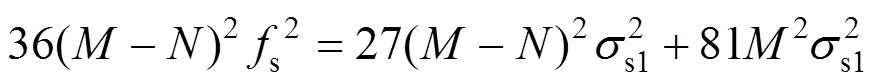
即：

同样在脱黏圆钢管中有：

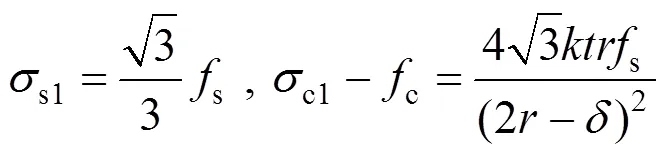
将式(29)代入式(28)即可得到优化后的脱黏圆钢管混凝土极限承载力公式：

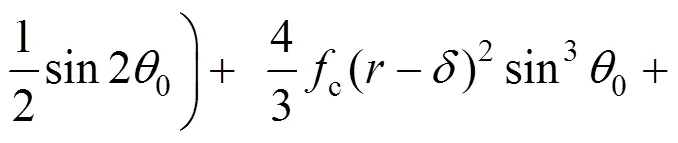
4 脱黏方钢管混凝土承载力计算公式

4.1 纵向静力平衡方程

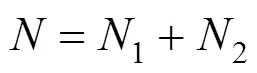
混凝土承载力1：

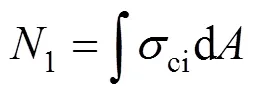
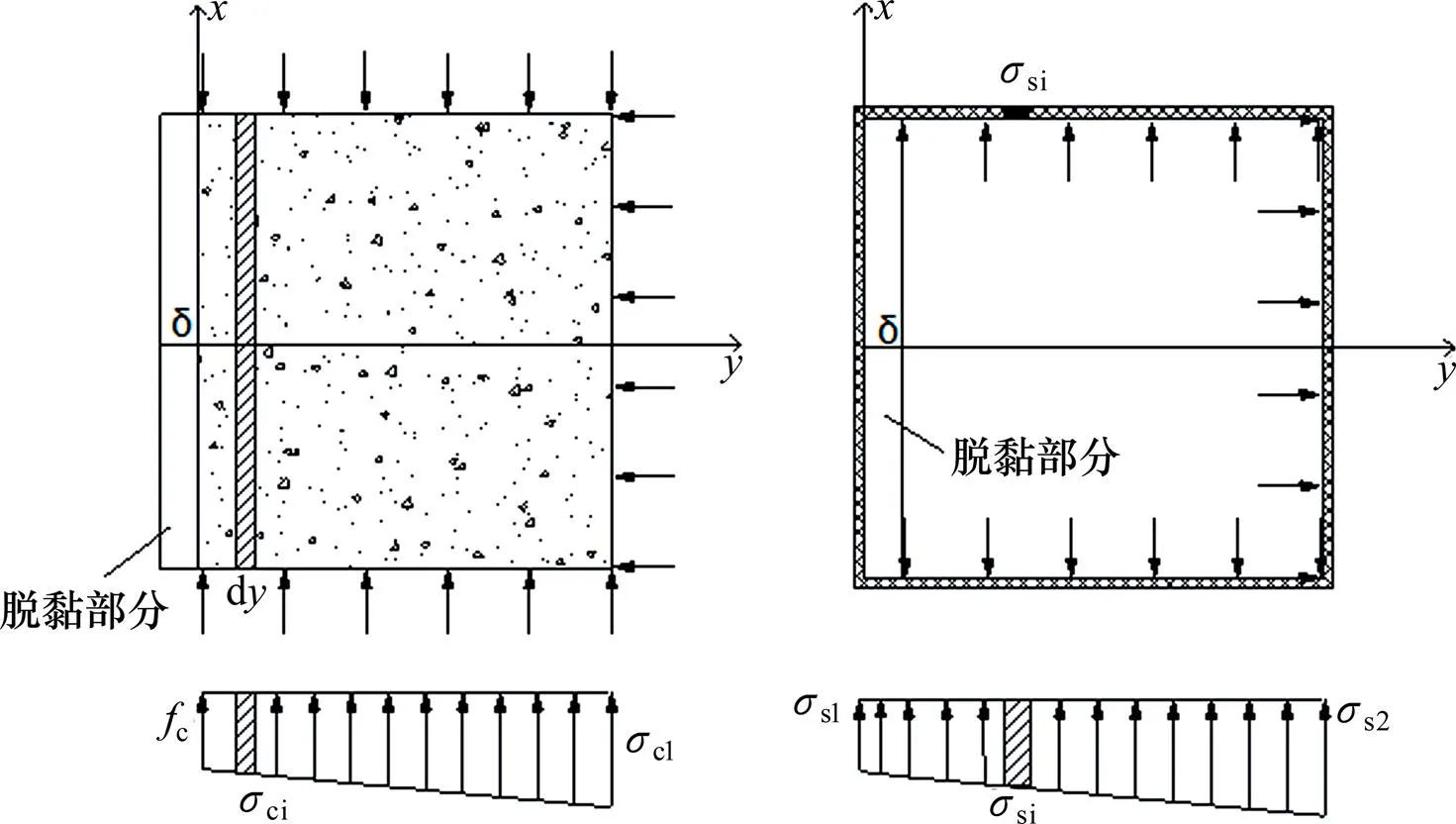
图5 核心混凝土和钢管计算简图

由几何关系可知：

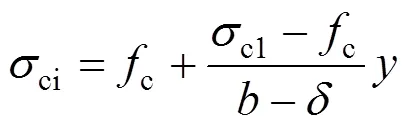
则有：

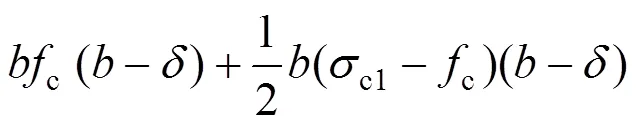
钢管承载力2：

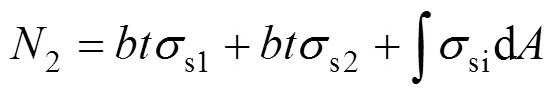
为简化计算，假定中间钢管受压强度线性变化，由几何关系可知：

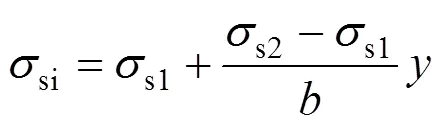
则有：

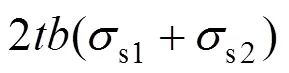
将式(32)和式(34)代入式(30)有：

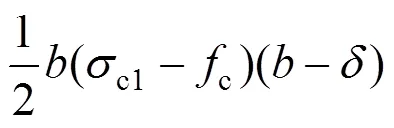
4.2 纵向弯矩平衡方程

由静力平衡条件，建立纵向弯矩平衡条件：

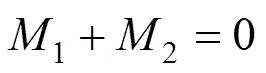
核心混凝土对中心轴的弯矩1：

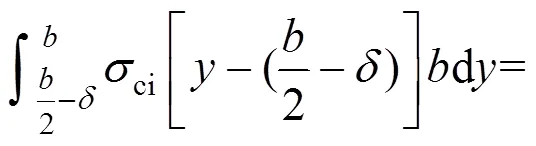
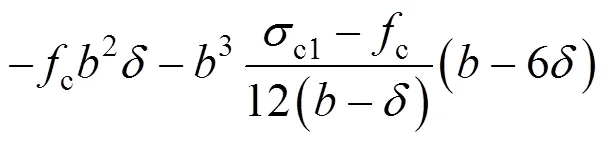
钢管对中心轴的弯矩2：

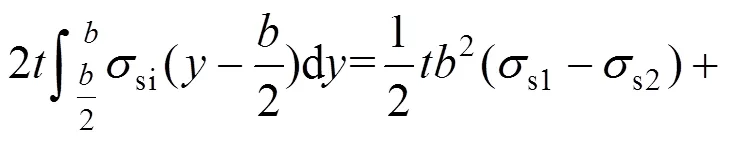
将式(37)和式(38)代入式(36)有：

将式(39)代入式(35)可以得到脱黏方钢管混凝土极限承载力：

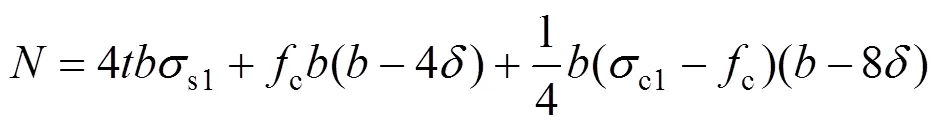
4.3 环向弯矩平衡方程

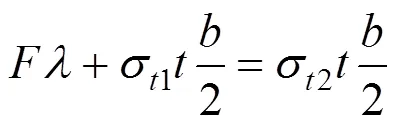
4.4 环向静力平衡方程

为简化用最大侧压力均匀计算，即=

4.5 脱黏钢管混凝土三向受力方程和钢管屈服 条件

脱黏钢管混凝土三向受力方程和钢管屈服条件和脱空情况相同，如式(15)和式(17)；

将式(17)代入式(42)有：

将式(17)和式(44)代入式(43)有：

化简得：

故：

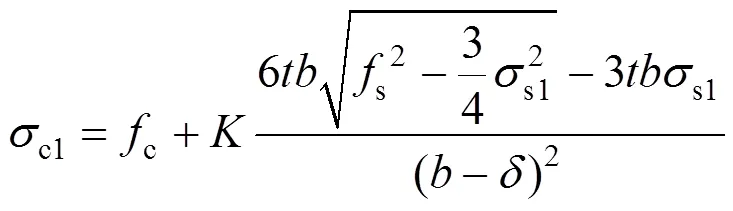
将式(45)两边同时对s1求导：

4.6 求解极值

由式(40)可见，荷载是钢管纵向应力s1的函数。我们的目标是求最大荷载max，于是将式(40)优化前的公式对s1取导数，并由极值条件：

令：

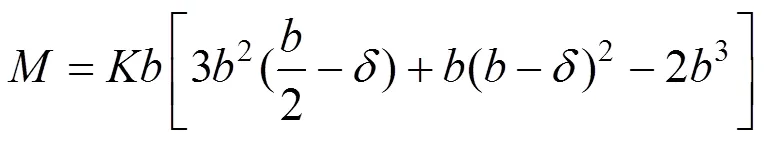
求解方程得：

即：

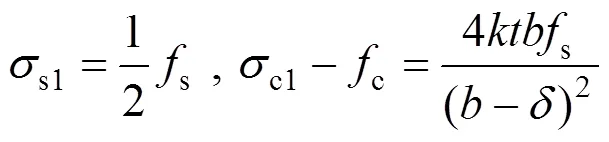
将式(48)代入式(40)即可得到优化后的脱黏方钢管混凝土极限承载力公式：

5 实例验证

5.1 公式校核

1) 圆钢管混凝土

图7 脱黏圆钢管缺陷率-SI曲线

表1和表2中分别列出了已有文献中的试验值和本文存在界面缺陷的钢管混凝土承载力计算值。从表中可以看出，本文计算值和试验值的误差基本都在8%以内，证明了本文推导的存在界面缺陷圆钢管混凝土极限承载力近似计算公式的可行性；

并且从缺陷率-曲线中可以发现，在脱黏钢管中，套箍系数越大缺陷对它的影响越大，且缺陷率小于一定值时，不同套箍系数的钢管混凝土承载力下降程度相近；在存在界面缺陷的圆钢管混凝土中，小缺陷情况下，承载力下降的更快，随着缺陷的变大，承载力下降变得缓慢。

2) 方钢管混凝土

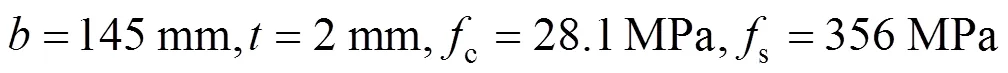
由于脱黏方钢管混凝土轴压试验未见报道，故没有文献进行验证，后续还需做试验进行验证。本文在表3中计算了一批上述参数的脱黏方钢管混凝土，列出了完好混凝土承载力计算值和本文存在界面缺陷的钢管混凝土承载力计算值以及承载力 折减。

表1 文献试验值与本文脱空承载力计算值对比表

表2 文献试验值与本文脱黏承载力计算值对比表

注：=缺陷钢管承载力/没有缺陷钢管承载力；是脱黏弧长率

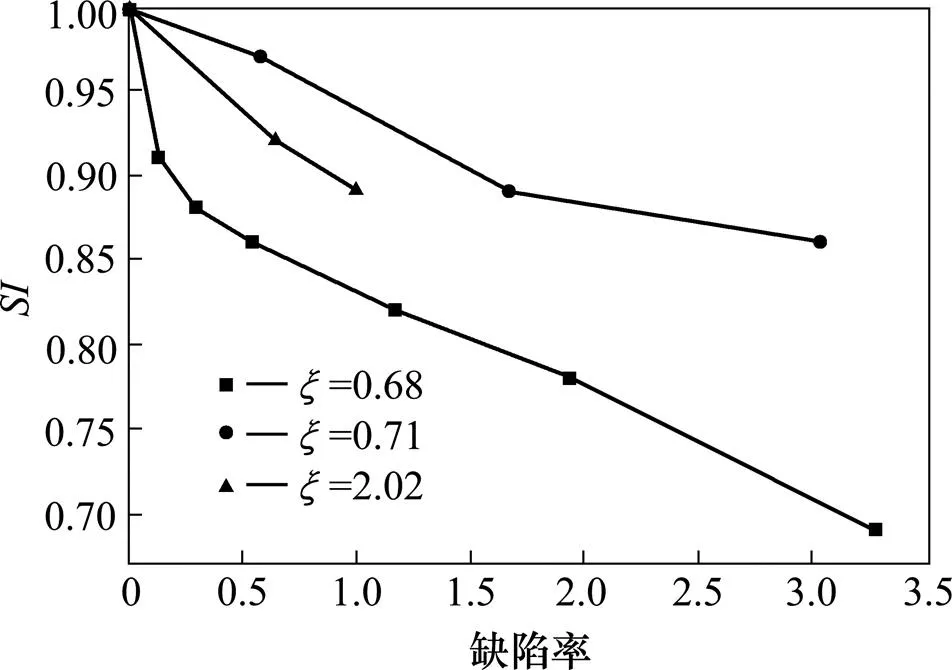
图8 脱空圆钢管缺陷率-SI曲线

表3 脱黏方钢管混凝土本文承载力计算值

5.2 计算结果分析

由上述本文计算值可以看出，随着缺陷率的变大其承载力也随之降低，这与目前已有的试验结论一致；总体来说对于存在界面缺陷的钢管混凝土极限承载力下降的原因可以归结为下面几点：

1) 核心混凝土面积减小；

2) 缺陷侧的套箍力减弱，使部分混凝土未能处于三向应力状态，导致钢管混凝土的整体套箍力减小；

3) 由于缺陷的存在，可能会发生屈曲现象； 对于存在界面缺陷的钢管混凝土来说，其荷载−轴向位移曲线大致可以分为5个阶段[12]：

阶段1 (-)：在这个阶段中，轴向荷载不断增加直到达到极限强度点；

阶段2 (-)：在这个阶段中，由于在缺陷侧缺乏钢管的约束作用，在点最薄弱处率先会有混凝土被压碎，此时轴向荷载突然下降约20%到达B点；

阶段3 (-)：在这个阶段中，随着破碎混凝土体积的扩大，膨胀混凝土开始与外钢管接触，钢管为其提供了约束，这种约束效应可以防止混凝土的进一步破碎，提高混凝土的强度和延性；

阶段4 (-)：在这个阶段中，在点另外一个薄弱处又会有混凝土被压碎，因此轴向荷载又会突然下降到达点；

阶段5 (-)：在这个阶段中，由于第2处破碎混凝土膨胀与外钢管接触，钢管为其提供了约束，使得轴向荷载再次增加直到点；

由上述分析可知钢管的套箍力是钢管混凝土承载力提高的关键因素，然而当出现界面缺陷的时候，套箍力会减弱直接导致极限承载力的下降，且钢管混凝土的挠度及纵向应变增大。当界面缺陷较小时，在受力调整后重新共同作用，如上面所形容的，此时危害还比较小。但当界面缺陷较大时，受力调整后仍不能共同受力，从而挠度和纵向应变的不连续性使钢管表面产生凸皱甚至发生屈曲现象，柱体产生偏心，承载力进一步下降，形成恶性循环。

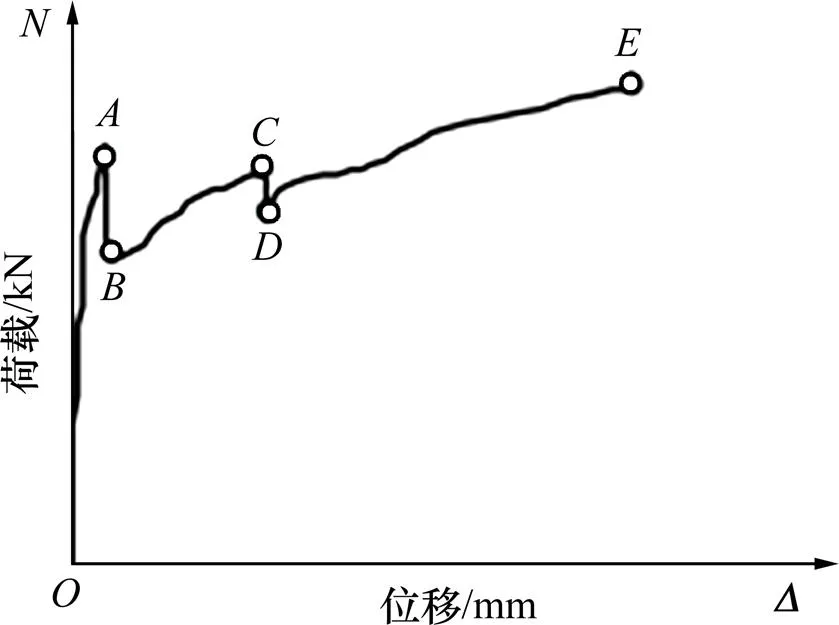
图9 荷载−轴向位移曲线

6 结论

1) 本文提出了界面缺陷钢管混凝土短柱轴心受压下极限平衡计算的基本假定，并根据钢管和混凝土的强度极限条件，建立了3种常见界面缺陷钢管混凝土轴压极限承载力计算公式。

2) 结合已有研究文献进行实例验证，结果表明用本文推导公式计算的承载力与文献试验值误差在8%以内，满足工程精度，验证了本文理论推导的可行性。

3) 综合分析了试验和计算极限承载力下降的原因，提出了界面缺陷钢管混凝土荷载−轴向位移曲线的五个阶段，并一一分析了每个阶段。

4) 本文在极限平衡理论基础上建立起的界面缺陷钢管混凝土轴压极限承载力计算公式，有一定的适用范围，即钢管没有发生整体屈曲现象。同时，仍需得到大量试验的验证和修正，为今后进一步研究界面缺陷钢管混凝土极限承载力提供了一种有效可行的方法。

[1] 韩林海. 钢管混凝上结构—理论与实践[M]. 北京: 科学出版社, 2004. HAN Linhai. Concrete structure of steel pipe coagulation-theory and practice[M]. Beijing: Science Press, 2004.

[2] 蔡绍怀. 现代钢管混凝土结构[M].修订版.北京: 人民交通出版社, 2007. CAI Shaohuai. Modern concrete-filled steel tubular structure[M]. Revised edition. Beijing: People’s Communications Press, 2007.

[3] 周绪红, 刘界鹏. 钢管约束混凝土柱的性能与设计[M].北京: 科学出版社, 2010. ZHOU Xuhong, LIU Jiepeng. Performance and design of concrete-confined concrete columns[M]. Beijing: Science Press, 2010.

[4] 叶跃忠. 混凝土脱粘对钢管混凝土中、低长柱性能的影响[J]. 铁道建筑, 2001(10): 2−5. YE Yuezhong. Effect of concrete debonding on the performance of low- and long columns in concrete-filled steel tubular[J]. Railway Engineering, 2001(10): 2−5.

[5] 薛俊青, 陈宝春, Briseghella Bruno. 脱粘钢管混凝土单圆管短柱偏压试验[J]. 建筑结构学报, 2009, 2(42): 237−241. XUE Junqing, CHEN Baochun, Briseghella Bruno. Compression test of short-walled concrete with single- tube concrete[J]. Journal of Building Structures, 2009, 2(42): 237−241.

[6] 杨世聪, 王福敏, 渠平. 核心混凝土脱空对钢管混凝土构件力学性能的影响[J]. 重庆交通大学学报(自然科学版), 2008, 27(3): 360−365. YANG Shicong, WANG Fumin, QU Ping. Effect of core concrete void on mechanical properties of concrete filled steel tubes[J]. Journal of Chongqing Jiaotong University, 2008, 27(3): 360−365.

[7] 梁柯峰. 脱空对钢管混凝土受力性能的影响[D]. 长沙:湖南大学, 2008. LIANG Kefeng. Effect of void on mechanical performance of concrete filled steel tubes[D]. Changsha: Hunan University, 2008.

[8] 刘夏平, 唐述, 唐春会, 等. 脱空钢管混凝土偏心受压力学性能试验研究[J]. 铁道建筑, 2011, 6(8): 41−46. LIU Xiaping, TANG Shu, TANG Chunhui, et al. Experimental study on eccentric compression mechanical behavior of concrete filled steel tubes[J]. Railway Engineering, 2011, 6(8): 41−46.

[9] 唐述. 脱空钢管混凝土力学性能研究[D]. 广州: 广州大学, 2001. TANG Shu. Study on mechanical properties of concrete-filled steel tube[D]. Guangzhou: Guangzhou University, 2001.

[10] LIAO Feiyu, LI Yongjin. Experimental behaviour of concrete filled steel tubes (CFST) with initial concrete imperfection subjected to eccentric compression[J]. Journal of Constructional Steel Research, 2012(35): 174−177.

[11] LIAO Feiyu, HAN Linhai, TAO Zhong. Behaviour of CFST stub columns with initial concrete imperfection: Analysis and calculations[J]. Thin-Walled Structures, 2013(70): 57−69.

[12] LIAO Feiyu, HAN Linhai, HE Shanhu. Behavior of CFST short column and beam with initial concrete imperfection: Experiments[J]. Journal of Constructional Steel Research, 2011, 67(12): 1922−1935.

[13] HAN Linhai, YE Yong, LIAO Feiyu. Effects of core concrete initial imperfection on performance of eccentrically loaded CFST columns[J]. Journal of Constructional Steel Research, 2016(7): 1943−1951.

[14] 易伟健. 混凝土结构试验与理论研究[M]. 北京: 科学出版社, 2012. YI Weijian. Experimental and theoretical study on concrete structures[M]. Beijing: Science Press, 2012.

[15] XUE Junqing, Bruno Briseghella, CHEN Baochun. Effects of debonding on circular CFST stub columns[J]. Journal of Constructional Steel Research, 2012(69): 64−76.

(编辑 蒋学东)

Theoretical derivation of ultimate bearing capacity of concrete filled steel tube with interface defects under axial compression

LU Jin, QIN Peng

(School of Civil Engineering, Hunan University, Changsha 410082, China)

The effect of the core concrete interface defect of the mechanical properties of the concrete filled steel tube is a hot topic at present. The ultimate bearing capacity of the concrete filled steel tube would decrease once it has the defects, i.e., the larger the defect, the more the bearing capacity would be reduced; however, there is no quantitative formula to calculate the bearing capacity with specific defects. Theoretical derivation of the ultimate bearing capacity of concrete filled steel tube with interfacial defects was put forward by means of the limit equilibrium method. The approximate formula for the ultimate bearing capacity of three different types of concrete filled steel tubular short columns with common interface defects was established. The results show that the basic trend of the load reduction deduced from this paper is the same as that of the testing values in the literature, which proves the theoretical derivation presented in this paper is feasible and accurate.

interface defect; concrete filled steel tube; limit equilibrium method; approximate calculation of bearing capacity

10.19713/j.cnki.43−1423/u.2018.09.019

TU392

A

1672 − 7029(2018)09 − 2316 − 11

2017−06−23

国家自然科学基金资助项目(51308201)；国家重点专项资助项目(2016YFC0701400)

秦鹏(1979−)，男，湖南常德人，讲师，博士，从事钢管混凝土结构和结构检测方面研究；E−mail：pengqin@hnu.edu.cn