基于SAGAFCM与主成分−熵的列车开行方案评价指标体系

李琳桦，符卓



基于SAGAFCM与主成分−熵的列车开行方案评价指标体系

李琳桦，符卓

(中南大学 交通运输工程学院，湖南 长沙 410075)

旅客列车开行方案评价指标体系是开行方案评价的基础，评价指标体系的建立和指标的选取直接影响到评价结果的准确性。现有的列车开行方案评价指标体系中，某些指标之间具有较强的相关性，为了避免该类指标对方案的某一方面做重复评价，需要对其进行分类和精简。根据评价指标之间的相互关系，采用基于遗传模拟退火算法的FCM算法对开行方案评价指标体系进行聚类简化，利用主成分分析法和信息熵法对其简化前后的信息量进行测量，得出保留原评价指标体系信息量相对较多的最佳简化评价指标体系。对文献中建立的评价指标体系进行重新简化，测试结果表明，重新构建的简化评价指标体系相较原简化评价指标体系能保留更多的信息量，证明了该方法的有效性。

铁路运输；列车开行方案；评价指标体系；SAGAFCM；主成分-熵

旅客列车开行方案，是指确定旅客列车运行区段、列车种类及开行对数的计划，是铁路旅客列车运营工作组织的重要内容[1]。开行方案的好坏直接关系到铁路旅客运输的经营效果和效益，因此有必要对旅客列车开行方案进行评价，为开行方案的优化与调整提供决策依据。旅客列车开行方案评价指标体系的建立是开行方案评价的基础，在现有的列车开行方案评价指标体系中，评价指标都比较多，如张萧萧[2]从效益、能力、技术和服务4个方面构建31个指标，童佳楠[3]从技术特性、服务特性和车流匹配3个角度构建37个指标。这些指标中某些指标之间具有较强的相关性和替代性，计算起来比较复杂。因此，为了使评价时抓住方案的主要因素对现有的开行方案进行调整[2]，有必要采取适当的方法找出评价指标体系中的关键性指标构成简化评价指标体系。一般来说，在选取指标构成简化评价指标体系时，通常会选择两两间相关性较弱的一组指标，使得简化之后的评价指标体系保留原评价指标体系尽可能多的信息量。若最终建立的简化评价指标体系的信息量损失过大，该评价指标体系也就失去意义。因此，如何构建合理的简化评价指标体系，最大程度地保留原评价指标的信息量，是一个值得探讨的问题。童佳楠等[3−4]利用SPSS软件对标准化后的指标进行聚类分析，从聚类分析得到的每一类指标中选取有代表性的指标作为典型指标，从而得到简化指标体系。王秀成等[5]在原指标体系中采用R聚类中的凝聚法对指标进行聚类，选取具有代表性的指标代替与其相关的其他指标，进一步简化了指标体系。HU等[6]通过分析影响旅客列车运行的各因素，从铁路运输企业经营效率和旅客服务质量2个方面综合构建城际客运列车开行方案评价指标体系。MENG等[7]列出一个复杂网络的度分布、网络路径的长度和聚类系数映射3个关键评价指标，并将它们与列车服务计划联系起来，定义了方便旅行程度、传输时间、旅行时间以及车站的聚类系数来评估列车服务计划。HUANG等[8]综合和改进相关研究后，尝试采用层次分析法和熵值法确定评价指标的主客观权重，建立列车开行方案评价指标体系，并基于偏差平方和，提出综合主观权重和客观权重的最优权组合方法，从而得到综合权重指标。在现有的旅客列车开行方案评价体系研究中，国外学者集中在评价指标体系的建立上，在评价指标的简化上还没有形成一套较为科学合理的方法，国内学者虽然对如何构造简化评价指标体系有所研究，但采用的聚类方法和在指标的选取上都包含有一定的主观因素，在简化理论方面还有待深入研究。因此，有必要在这些已有研究成果的基础上，对旅客列车开行方案评价指标体系做进一步探讨。本文尝试构建一种较为客观的列车开行方案评价指标简化方法。采用基于遗传模拟退火算法的FCM算法(SAGAFCM算法)对原始数据进行聚类，从每一个聚类类别中分别选出一个指标构成简化评价指标体系，通过利用主成分分析法和信息熵法测量简化前后评价指标体系的信息量，计算得出保留原评价指标体系信息量最多的一组简化评价指标体系作为最佳简化评价指标体系。以文献[2]中建立的单方案评价指标体系作为算例，对其评价指标体系进行重新简化，并在对比分析的基础上，重新构建简化评价指标体系。

1 列车开行方案评价指标简化思路

在对旅客列车开行方案进行简化的实际操作中，指标之间的相关性难以量化，各评价指标对列车开行方案的评价指标体系的信息贡献量和各指标之间的信息重叠量也难以测量。因此，本文需要解决2个科学问题：一是如何对指标进行分类；二是如何从各个分类中选择合适的指标作为典型指标构成简化评价指标体系，从而对评价指标体系进行精简。

1.1 指标的分类

对于指标的分类，可采用聚类分析法对评价指标体系进行研究。本文通过对比分析的基础上，采用SAGAFCM算法，该方法利用模拟退火算法较强的局部搜索能力和遗传算法较强的全局搜索能力，有利于克服FCM方法对初始聚类中心的敏感性、人为因素影响和容易陷入局部最优等缺陷。

1.2 典型指标的选取

在对列车开行方案评价指标体系进行聚类分析的基础上，对得到的每类指标中选取具有代表性的指标作为典型指标，这样既能避免对方案的某一方面做重复的考查，也能简化操作。在以往的文献中，典型指标的选取往往凭借人的主观判断进行选择。考虑到简化列车开行方案评价指标体系是在原列车开行方案评价指标体系的基础上筛选得来的，因此可以通过测算简化评价指标体系的信息量相对原评价指标体系的信息贡献率，选取信息贡献率最大的一组简化评价指标体系，则其所保留的原评价指标体系的信息量也最多，由此作为典型指标选取的依据。简化评价指标体系和原评价指标体系信息量的测量，需要解决2个问题：一是如何消除指标体系的相关性；二是如何测算一组互相独立的指标体系的信息量。基于此，本文结合主成分分析方法和信息熵方法，利用主成分变换将指标间的相关性进行消除，然后利用信息熵法对这组相互独立的指标体系的信息量进行测量，利用该方法便能测量出简化前后2个指标体系的信息量[9]。

2 列车开行方案评价指标简化方法构建

对列车开行方案评价指标体系简化方法的构建，主要可分为2步进行。第1步，采用SAGAFCM算法对原评价指标体系进行聚类；第2步，利用主成分——熵法测量每一个简化评价指标体系的信息量，选取出保留原评价指标体系信息量最多的，作为最佳简化评价指标体系。

2.1 评价指标体系的聚类——基于遗传模拟退火算法的FCM算法

列车开行方案评价指标体系中，指标与指标之间存在的相关性难以量化，很容易导致评价用户对方案的某一方面做过多且重复的评价工作。因此，选取合适的指标作为典型指标的首要步骤，就是要对原评价指标体系中的所有评价指标进行聚类 分析。

聚类以相似性为基础，将一个数据集按照某个特定的准则进行分割，变成不同的类或簇，聚类后会将同一类的数据尽可能聚集到一起，不同数据尽量分离。目前，从准确度方面考虑，在较为主流的聚类方法中，FCM算法相对优于其他方法，但这种方法对初始聚类中心敏感、容易受人为因素影响和陷入局部最优。因此本文选择在FCM方法的基础上融入模拟退火算法和遗传算法，即SAGAFCM算法，在调整优化种群的同时可以预防其过早地收敛，对列车开行方案评价指标体系中的指标进行聚类。

SAGAFCM算法思想是根据简化评价指标体系中指标的数量确定聚类的类别数，将相似程度较高的指标归为一类，经过不断地反复迭代和修改计算指标的聚类中心和隶属度[10]，然后进行重新分类，当算法收敛时，就完成了模糊聚类划分，得出全局近优解。具体实现过程如下。

Step 1：初始化控制参数：种群个体大小，最大进化次数，交叉概率c，变异概率m，退火初始温度0，温度冷却系数，终止温度end。

Step 3：设置循环计数变量=0。

Step 5：若＜，则=+1，转至Step 4，否则转至Step 6。

Step 6：若T＜end，则算法结束，返回到目前为止搜索到的最好解；否则，执行降温操作T+1=kT，转至Step 3。

2.2 评价指标体系信息量的测量——基于主成 分−熵

合理地简化评价指标体系一般能够保留原评价指标体系较多的信息量。从2.1中所得到的聚类的每一个类别中分别选取一个指标，即可构成一个指标数为的简化评价指标体系，设这些简化评价指标体系所有可能结果构成一集合，={1，2，…，JH}，其中为指标数为的简化评价指标体系个数。如何从这种可能中选出保留原评价指标信息量最多的简化评价指标体系，就需要对简化前后评价指标体系的信息量进行测量。关于信息量的测量方面，国内外一些学者都提出了用热力学概念——熵来度量。Dehmer等[11]描述了熵测度的广泛适用性，通过对一些熵测度经典方法的回顾，论证了熵在包括生物学、化学和社会学等各种领域中发挥的重要作用，王炜等[13]通过熵权法确定各影响因素权重，将熵应用在公路隧道竖井开挖施工方案中。

因此，本文也考虑将熵应用于旅客列车开行方案评价指标体系中，来测量评价指标体系的信息量。测量评价指标体系信息量，首先需要消除指标之间的相关性，再对一组相互独立的指标的信息量进行测量。基于此，考虑采用主成分分析法消除指标之间的相关性，再利用信息熵法计算原评价指标体系和简化评价指标体系的信息量，后者比上前者，即为简化评价指标体系相对原评价指标体系的信息贡献率。测量信息量方法的具体过程如下：

1) 采用标准差标准化方法(即Z-score 标准化)对原评价指标体系的各个指标值进行标准化处理，把数据无量纲化，得到标准化后的指标{1,2,…,Y}。

2) 将标准化后的指标进行主成分变换[13]，得到主成分指标数据矩阵=(f)p×q，f表示第个主成分变量F的第个样本数据，其中f的打分公 式为：

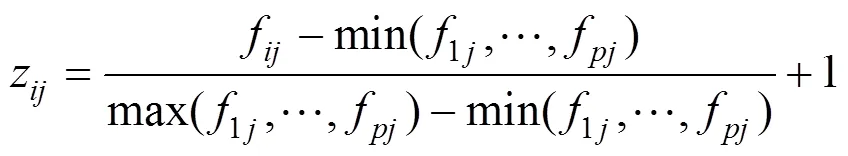
经过主成分变换将相关的一组指标变成了一组线性无关的新变量，并且不改变原始指标的信息量[9]。

3) 用信息熵法计算单一主成分指标的信息量。

设(F)为第个主成分变量F的熵，则其值可由下式计算得到：

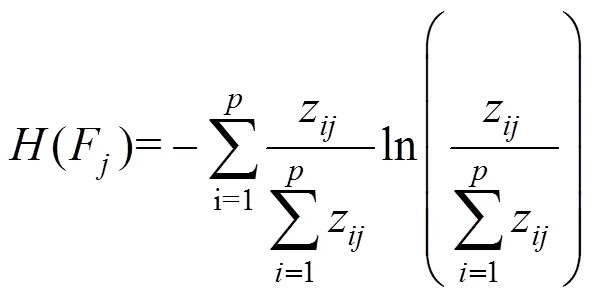
设(F)为第个主成分变量F的信息量，根据信息量测量方法，指标数据的信息量为最大熵值与当前熵值的差[14]，由此可得：

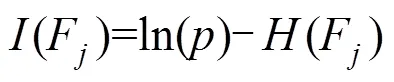
4) 计算指标体系的信息量。设为指标体系{1,2,…,Y}的信息量，因为{1,2,…,Y}服从多元正态分布，则等于其每个对应主成分指标{1,2,…,F}的信息量之和，即：

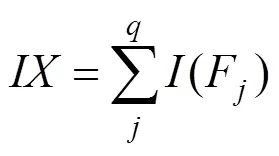
文献[9]对式(4)的正确性进行了具体的证明，本文不再赘述。

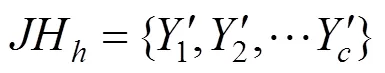
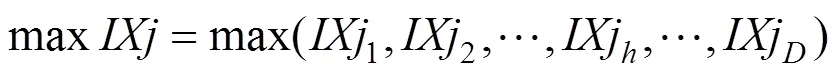
6) 计算max对原评价指标体系的信息贡献率

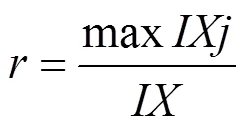
反映了简化评价指标体系的信息量占原评价指标体系信息量的比重。为避免信息的损失，本文将采取累计贡献率100%的方式选取主成分变量。

综合2.1和2.2，即为基于SAGAFCM算法和主成分−熵的列车开行方案评价指标体系的简化方法，具体实现流程图如图1所示。

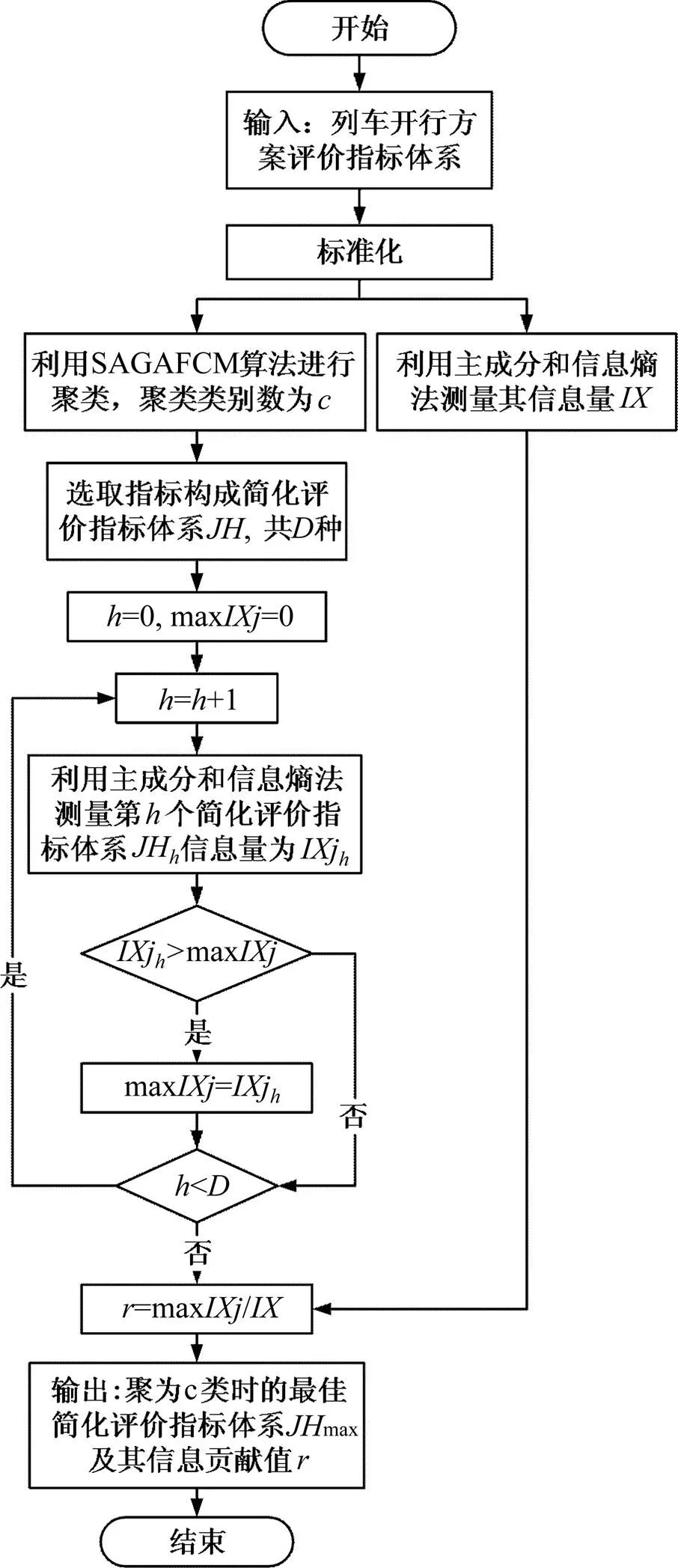
图1 旅客列车开行方案评价指标体系简化流程

3 算例分析

本文所描述的方法已用matlab编程实现。在算例数据采集方面，文献[3]研究的是事前评估，故采用客流分配技术得到每列车的客流数据,而不是实际的运营统计数据作为评价基础；文献[4−5]的评价指标体系未考虑车底运用方面等技术指标。因此，从数据的准确性和评价指标体系的完整性2方面综合考虑，本文以文献[2]中的指标体系为算例。该文献建立的原评价指标体系中，共有40个样本，每一个样本均有22个评价指标,具体每个样本的指标值参见文献[2]，表1列出了该评价体系的22个评价指标。

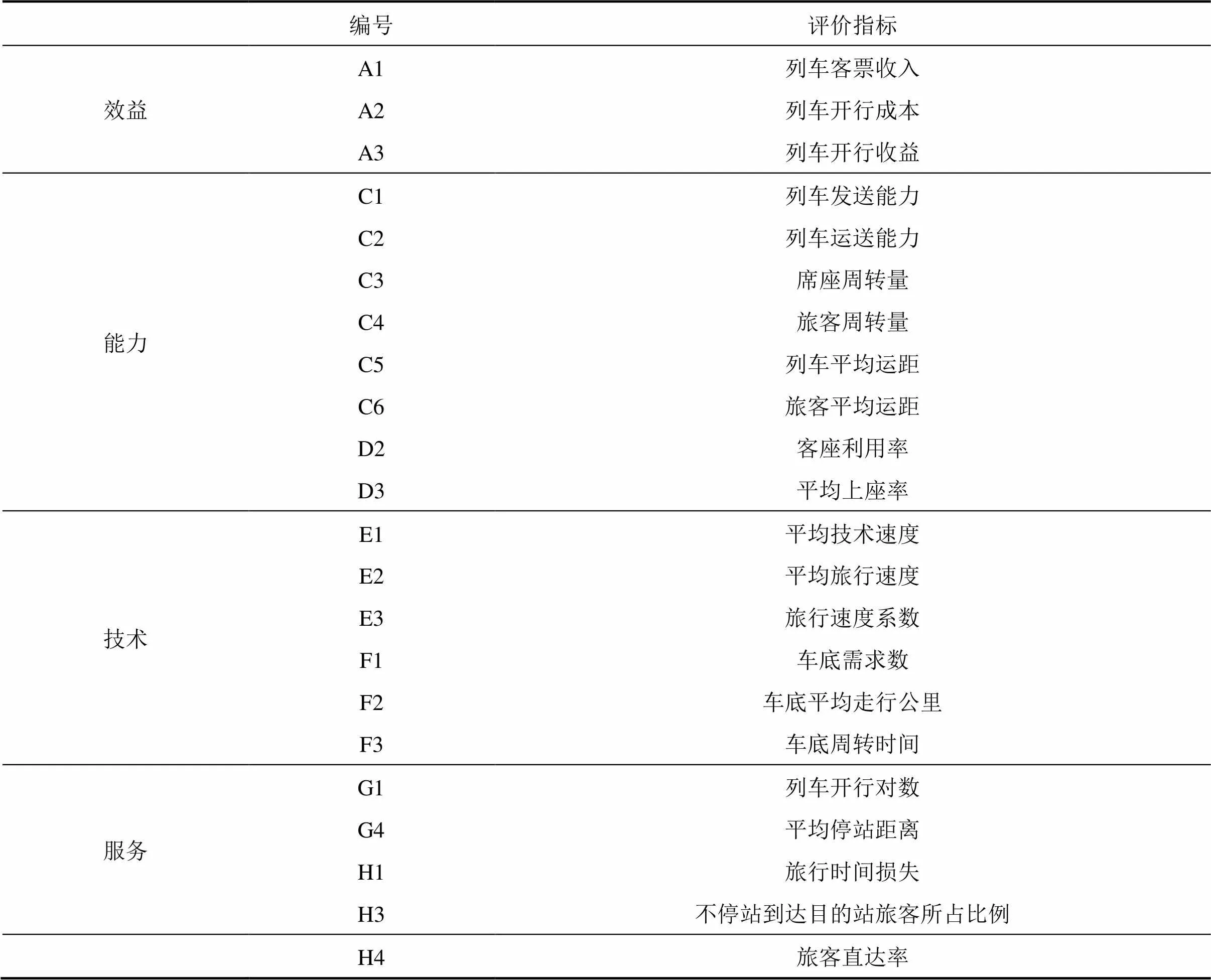
表1 原列车开行方案评价指标体系数据

在文献[2]中，作者采用SPSS对原评价指标体系中的数据进行聚类，从聚类分析得到的每类指标中选取有代表性的指标作为典型指标，以此来进行简化操作，减少对列车开行方案某一方面评价的重复性，得到简化评价指标体系中的5个指标，分别为：A3列车开行收益，C1列车发送能力，D3平均上座率，F1车底需求数和H4旅客直达率。

本文通过主成分分析和信息熵法对文献[2]建立的简化评价指标体系相对原评价指标体系的信息贡献率进行计算，得=0.247 8，结果表明，文献[2]的简化评价指标体系只保留了原评价指标体系24.78%的信息，信息损失较为严重。

本文通过SAGAFCM算法对该算例进行简化，分别计算指标数量为5-8以及10和13的最佳简化评价指标体系，计算时间最长不超过30 s。求解过程如图1所示，其结果如表2所示。

表2 不同指标数的最佳简化评价指标体系

利用本文所描述的方法，求得该算例保留5个指标时的最佳简化评价指标体系：C1列车发送能力、C2列车运送能力、E2平均旅行速度、F2车底平均走行公里和H1旅行时间损失。该简化后的指标体系相对于文献[2]中选取的5个指标有所不同，保留的信息量较原文中的24.78%提升了7%左右，但也只保留了原评价指标信息量的31.63%，信息失真也较为严重。

可见，如果只选取5个指标对列车开行方案进行评价，并不能对列车开行方案起到很好的评价效果。从表2中可以看出，随着指标数的增加，信息贡献率越大，而当简化评价指标数大于8个时，指标数增加率越来越大于信息贡献率的增加速率，增加指标并不能有效提升列车开行方案简化评价指标体系相对原列车开行方案评价指标体系信息贡献率。当列车开行方案简化评价指标体系中指标数量为8个时，其最佳简化评价指标体系相对原评价指标体系的信息贡献率为48.3%，保留的信息量相对较高。相对于文献[2]，只增加了3个指标，保留的信息量却多了将近1倍。因此，本文建议对文献[2]所建立的简化评价指标体系进行重新构建，综合考虑选取的指标数及其所对应的信息贡献率，可考虑选取A2，C1，C2，C5，C6，E2，F2和H1等8个指标构成简化评价指标体系，这样可使简化后的评价指标体系更具有代表性。若以给定的信息贡献率为选取指标数的标准，则可用本文所提出的方法进行计算，得出类似于表2所示的结果，对应选取即可。

4 结论

1) 在对旅客列车开行方案评价指标进行聚类时，本文区别于以往的SPSS、凝聚法等聚类方法，采用基于遗传模拟退火算法的FCM算法(SAGAFCM算法)，该方法同时拥有模拟退火算法较强的局部搜索能力、遗传算法较强的全局搜索能力以及FCM方法的高准确性，较好地克服了一般聚类算法对初始聚类中心敏感、人为因素影响、容易陷入局部最优等缺陷，使聚类结果更为科学 合理。

2) 引入信息熵的概念，对旅客列车开行方案评价指标体系的信息量进行测量。将旅客列车开行方案中评价指标包含的信息量数量化，借助数学工具——熵来度量单一评价指标的信息量以及整个评价指标体系的信息总量，使评价指标体系简化结果更有说服力。

3) 将SAGAFCM算法、主成分分析法和信息熵法进行结合，构建一种新的旅客列车开行方案评价指标体系简化方法，通过聚类、测量信息量，对比同一指标数量下的列车开行方案简化评价指标体系相对原列车开行方案评价指标的信息贡献率，选取信息贡献率最高的列车开行方案简化评价指标体系，作为该指标数量下的最佳列车开行方案简化评价指标体系。实际样本验算表明，该方法能在较短的时间内计算出保留原列车开行方案评价指标体系信息量相对较多的不同的简化评价指标体系，供最终选取时参考。

[1] 王甦男. 旅客运输[M]. 北京: 中国铁道出版社, 2005.WANG Sunan. Passenger transportation[M]. Beijing: China Railway Press, 2005.

[2] 张萧萧. 高速铁路列车开行方案评价方法及系统开发[D]. 北京: 北京交通大学, 2011. ZHANG Xiaoxiao. Evaluation of high-speed railway passenger train service plan and system development[D]. Beijing: Beijing Jiaotong University, 2011.

[3] 童佳楠. 基于配流技术的高速铁路列车开行方案评估及系统实现[D]. 北京: 北京交通大学, 2016. TONG Jianan. Evaluation of high-speed railway line plan based on passenger flow assignment and system development[D]. Beijing: Beijing Jiaotong University, 2016.

[4] 邓连波, 史峰. 旅客列车开行方案评价指标体系[J]. 中国铁道科学, 2006, 27(3): 106−110. DENG Lianbo, SHI Feng. Evaluation index system of passenger train operation plan[J]. China Railway Science, 2006, 27(3): 106−110.

[5] 王秀成, 贺振欢, 聂磊, 等. 多层次高速铁路列车开行方案评价及优化方法研究[J]. 铁道运输与经济, 2016, 38(8): 13−18. WANG Xiucheng, HE Zhenhuan, NIE Lei, et al. Study on evaluation and optimization method of multi-level High-Speed railway train operation program[J]. Railway Transport and Economy, 2016, 38(8): 13−18.

[6] HU Z, YAN Y, LIU Y, et al. Fuzzy comprehensive evaluation of inter-city passenger train operation plan[C]// International Conference on Transportation Engineering, 2007: 711−716.

[7] MENG X, QIN Y, JIA L. Comprehensive evaluation of passenger train service plan based on complex network theory[J]. Measurement, 2014, 58: 221−229.

[8] HUANG X, LAN S, LI B. Evaluation of train running plan for passenger-dedicated railway line based on optimal weights combination method[C]// International Conference on Transportation Engineering, 2015: 2045− 2050.

[9] 迟国泰, 李战江. 基于主成分——熵的评价指标体系信息贡献模型[J]. 科研管理, 2014, 35(12): 137−144. CHI Guotai, LI Zhanjiang. Model of information contribution of evaluation index system based on principal component-entropy[J]. Science Research Management, 2014, 35(12): 137−144.

[10] 史峰, 王辉, 郁磊, 等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011: 178−196. SHI Feng, WANG Hui, YU Lei, et al. 30 cases analysis of MATLAB intelligent algorithm[M]. Beijing: Beihang University Press, 2011: 178−196.

[11] Dehmer M, Mowshowitz A. A history of graph entropy measures[J]. Information Sciences, 2011, 181(1): 57−78.

[12] LIANG Z, DUAN X, LI X. Entropy measures in neural signals[M]. Signal Processing in Neuroscience. Springer Singapore, 2016.

[13] 王炜, 陈建平, 余亚东, 等. 熵权模糊综合评价法在竖井施工方案比选中的应用[J]. 铁道科学与工程学报, 2016, 13(9): 1776−1781. WANG Wei, CHEN Jianping, YU Yadong, et al. Application of entropy-weight and fuzzy comprehensive evaluation method in the selection of shaft construction schemes[J]. Journal of Railway Science and Engineering, 2016, 13(9): 1776−1781.

[14] 高慧璇. 应用多元统计分析[M]. 北京: 北京大学出版社, 2005: 16−290. GAO Huixuan. Multivariate statistical analysis[M]. Beijing: Beijing University Press, 2005: 16−290.

[15] 张良,蔡生.信息量的度量及应用[J]. 沈阳大学学报, 2004,16(2): 89−91. ZHANG Liang, CAI Sheng. Measurement and application of information quantity[J]. Journal of Shenyang University, 2004, 16(2): 89−91.

(编辑 阳丽霞)

Evaluation index system of train plan based on SAGAFCM and principal component-entropy

LI Linhua, FU Zhuo

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

The evaluation index system of passenger train plan is the basis of the evaluation of train plan. The establishment of evaluation index system and the selection of indexes directly affect the accuracy of the evaluation results. In case of repeated examination on index of one aspect of the program, some indicators that have relevance to another in the existing train plan evaluation index system need to be classified and streamlined. The FCM algorithm based on genetic-simulated annealing algorithm was adopted to cluster and simplify the evaluation index system of the train plan according to the correlation between the evaluation indices. Principal component analysis and information entropy method were used to measure the amount of information before and after the simplified evaluation index system. The relatively good simplified evaluation index system with the most information of the original evaluation index system was obtained. The evaluation index system in the literature is re-simplified. The results show that the restructured simplified evaluation index system can retain more information compared with that in the literature, which proves the effectiveness of the method.

railway transportation; train plan; evaluation index system; SAGAFCM; principal component- entropy

10.19713/j.cnki.43−1423/u.2018.09.033

U293.1

A

1672 − 7029(2018)09 − 2432 − 07

2017−07−02

国家自然科学基金高铁联合基金资助项目(U1334207)；国家自然科学基金资助项目(71271220)

符卓(1960−)，男，海南文昌人，教授，博士，从事交通运输规划与管理研究；E−mail：zhfu@csu.edu.cn