加速度数据误差对弹道积分解算的影响分析

2018-10-08房立清霍瑞坤

火炮发射与控制学报 2018年3期

徐磊，房立清，霍瑞坤，李旭

(陆军工程大学石家庄校区，河北石家庄 050003)

现代化战争的创新变化，使得战争模式不断向着信息化方向发展，瞬息万变的的战场形式对弹药的高效毁伤能力和精确打击能力提出了更高的要求，弹药更趋向于智能化制导化[1]。实时准确获取弹丸的加速度值，在解算弹丸飞行姿态、对弹丸进行实时修正、实现惯性导航等方面发挥着重要作用。

利用加速度传感器实现弹丸加速度的采集是当前比较精确的获取手段，通过对加速度双重积分以实时解算弹丸运动状态的方法在各种弹丸中得到广泛应用。在弹道修正引信中利用加速度计测得弹丸轴向加速度，通过数值积分方法得出理论射距，进而与预定射距相比较，对弹丸的射程进行修正，达到提高射击精度的目的[2]；在硬目标计行程侵彻引信中，弹丸碰撞目标时实时采集侵彻弹丸的加速度值，利用积分算法计算弹丸实际穿透的行程，识别弹丸穿透目标的状态，确保弹丸在预定位置起爆，实现炸点的精确控制[3]；在惯性导航系统中，加速度传感器作为必不可少的器件发挥着越来越重要的作用。对于捷联式惯导系统而言，利用由加速度计和角速度计组成的测量单元对载体的运动姿态进行实时获取，通过对加速度的积分得到载体的速度、角速度以及位置等信息[4]；由于陀螺仪漂移严重，量程小，因此无陀螺惯导系统则完全利用加速度计完成测量任务，利用加速度计的安装位置不同得到的不同加速度计算出载体的姿态信息，实现对载体的导航[5-6]。

弹丸加速度作为弹道的重要参数，有必要对其进行误差分析，以确保在利用其进行弹道解算实现弹药的定点定距打击等功能时具有较高的精度。对误差进行分析处理提高测试精度方面的研究，主要包括优化积分算法,即对于时频域积分的选择以及梯形或者矩形等各种积分公式的选择；分离误差即利用最小二乘法、EMD分解法、傅里叶级数逼近法等[7]方法对积分信号中的误差进行分离；安装误差即合理配置加速度计数量，提高加速度的标定精度，优化补偿算法等[8]。在对传感器误差研究中，很少有专门对数据输出特性以及数据误差在积分后带来的影响进行分析，然而这种误差在弹道解算时是不可避免的，为此，基于弹丸刚体六维外弹道模型，在1 500 m范围内进行弹道积分解算，为使积分偏差在5‰以下，对加速度传感器的频率以及加速度采集误差呈正态分布、线性分布和正弦分布时对积分产生的误差进行分析，得出传感器应该满足的条件。

1 外弹道模型的建立

为了准确分析加速度积分中弹道弧长与水平飞行距离的关系，依据文献[9]建立刚体外弹道模型，其中的公式推导与变量定义不再赘述。

(1)

(2)

在进行有关利用加速度传感器测量的加速度进行积分时设置攻角为0，根据牛顿运动定律，可得出弹丸加速度与受力之间的关系：

(3)

2 仿真数据分析

2.1 传感器的数据更新频率分析

传感器的更新频率是加速度积分精度的重要影响因素，从理论上讲频率越大精度越高，但是在真实运用中，不可能无限大，为仿真得到1 500 m条件下误差标准的要求，选择30、40、50、100、200、300 Hz 6种频率参数对弹丸弹道弧长进行仿真计算。

从图1～2中可以看出加速度数据更新频率对弹丸弹道弧长积分精度及水平飞行距离精度有较大影响。

更新频率为30 Hz时，其产生的弹道弧长积分偏差及水平飞行距离偏差分别为7.7、7.5 m；更新频率为300 Hz时，其产生的弹道弧长积分偏差及水平飞行距离偏差分别为0.74、0.72 m。为满足1 500 m积分偏差在5‰以下的要求，加速度更新频率不能低于30 Hz；如果单项误差不能超过1 500 m定距偏差1/10，则加速度数据更新频率不能小于300 Hz。

2.2 加速度数据的采集误差分析

利用加速度传感器采集运动物体加速度时会存在一定的偏差，采集误差会对弹道积分弧长产生较大影响，为了具体分析采集误差的影响，选取常见的正态分布、线性分布和正弦分布3种分布方式，对弹道弧长进行仿真计算分析。

2.2.1 加速度采集误差呈正态分布

图3、4给出了均值误差为0，方差分别为σ2=5、10、15、20时，其对弹道积分弧长偏差及水平飞行距离偏差的影响。

由于产生正态分布的随机数具有随机性，故其产生的弹道弧长积分误差正负也具有随机性。从图3、4中可以看出，当均值为0，方差从5～20不等时，加速度采集误差引起的弹道积分弧长偏差及水平飞行距离偏差不同，方差越大，积分弧长偏差及距离偏差越大。为满足1 500 m积分偏差在5‰以下的要求，加速度误差呈均值为0的正态分布时方差值不能超过20，即σ≤4.47 m/s2。

2.2.2 加速度采集误差呈线性分布

图5～6给出了加速度数据误差呈线性变化，初始时刻误差为0，弹道末期误差分别为0.035、0.105、0.315、0.945 m/s2时，弹道积分弧长偏差与水平飞行距离偏差的曲线。

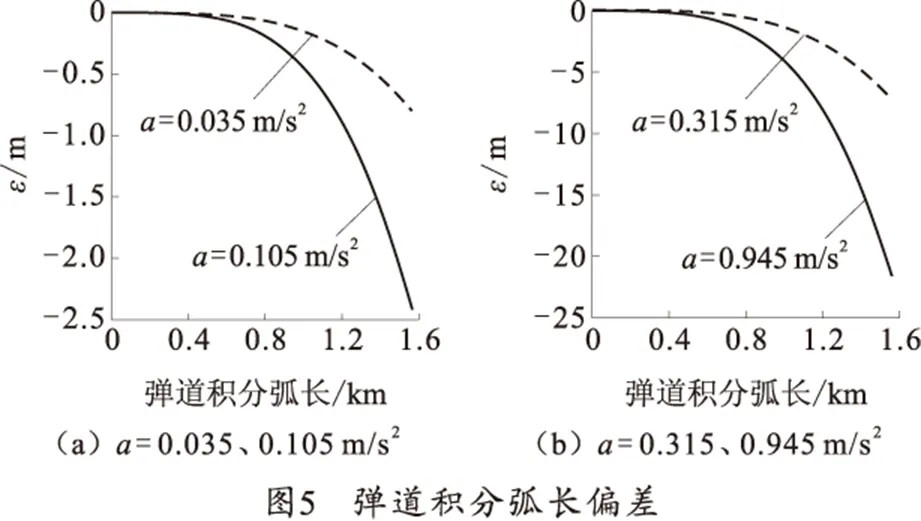
从图5、6中可看出，随着飞行距离增大，由加速度误差引起的弹道积分弧长偏差和水平飞行距离偏差迅速增大。从图中可以看出在不同加速度误差下水平飞行距离偏差随飞行距离数值的变化，当弹道末期加速度误差分别为0.035、0.105、0.315、0.945 m/s2时，在1 500 m射距上引起的距离偏差分别为-0.75、-2.24、-6.71、-20.122 m。为满足1 500 m积分偏差在5‰以下的要求，加速度误差呈线性分布时，其弹道末期误差不能超过0.035 m/s2，即aerror≤0.035 m/s2。

2.2.3 加速度采集误差呈正弦分布

正弦分布是最常见分布的之一，也是最容易出现的误差分布之一。假设加速度数据误差呈正弦函数前1/4周期变化，如图7所示。

加速度数据误差起始值为0，弹道末期误差值(即正弦信号幅值)分别取0.025、0.075、0.225、0.675 m/s2，图8、9给出了弹道积分弧长偏差与水平飞行距离偏差的曲线。

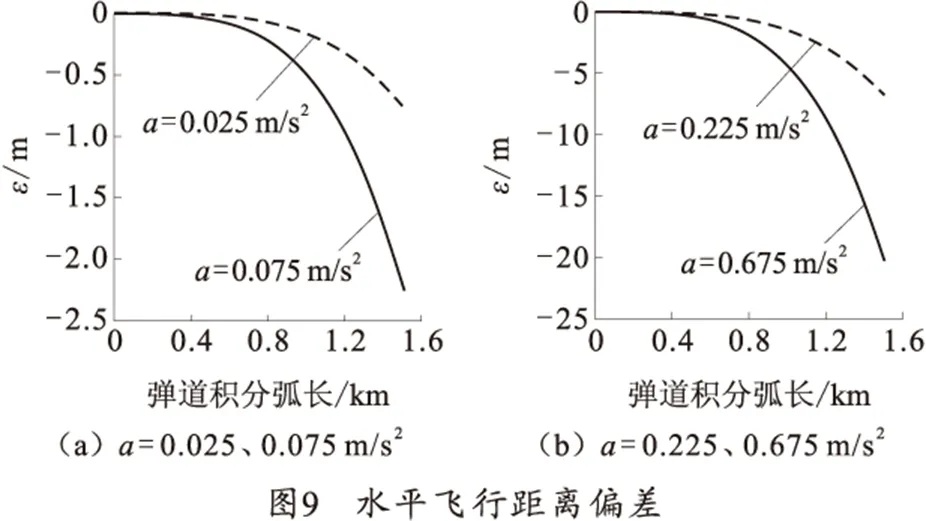
从图8、9可看出，弹道积分弧长偏差和水平距离偏差随着飞行距离的增大而迅速增大，且跟前面几种加速度误差引起的距离偏差规律相似。在1 500 m飞行距离上，误差幅值为0.025 m/s2时引起的水平距离偏差为0.75 m；误差幅值为0.225 m/s2时引起的水平距离偏差为6.67 m。水平距离的偏差随着加速度误差的增大而增大，且两者满足很好的线性关系。为满足1 500 m积分偏差在5‰以下的要求，加速度误差呈正弦分布时，其弹道末期误差不能超过0.025 m/s2，即aerror≤0.025 m/s2。