电磁轨道炮内弹道模拟及初速误差分析

陈丽艳，杨 帆，王 端

(中国电子科技集团公司第二十七研究所，河南 郑州 450047)

电磁轨道炮的内弹道发射过程，为电枢速度、脉冲电源放电电流、时间、推力和摩擦力等多元素相互耦合的过程。对电磁轨道炮的内弹道模拟，需要将运动弹丸作为脉冲电源的动态负载，将洛伦兹力加速的动力学及运动学方程与电路方程结合起来求解。

电枢的初速散布是影响电磁轨道炮打击精度的重要因素。引起电枢初速散布的因素包括脉冲电源系统的电参数漂移、发射器和电枢等器件在生产制造和使用的过程中存在误差等[1]。

笔者建立了基于MATLAB的电磁轨道炮内弹道仿真模型，对电磁轨道炮的动态发射过程进行了数值模拟；分析了影响电磁轨道炮电枢初速精度的主要因素，采用蒙特卡洛法进行了内弹道随机模拟，对电枢的初速散步进行预测，就系统参数的随机散布对电枢初速的影响进行了定量分析；并通过误差设计技术，提出对各参量的定量指标要求，以达到控制误差，提高发射精度的目的。

1 电磁轨道炮误差源分析

电磁轨道炮基于法拉第电磁感应定律，导电电枢在两根平行导轨产生的强磁场内获得电磁力，从而完成对电枢的加速，如图1所示。电磁轨道发射是一个涉及电磁学、动力学、材料等多种问题的复杂过程，存在轨道间强脉冲电流、电枢和电枢滑动摩擦等复杂载荷的作用。电磁轨道炮由大功率充电单元、脉冲成形网络、电磁轨道发射器以及一体化电枢组成。

引起电枢初速散布的随机因素主要包含以下几方面内容：

1)受加工误差、装配误差以及炮体振动、轨道变形等因素影响，发射器的轨道电阻、轨道电感存在随机波动。

2)受环境、温度等因素影响，脉冲电源的电容量、电阻、电感存在随机波动。

3)充电单元存在控制误差，电容器在充电、保压过程中存在能量泄漏，会引起放电电压的随机波动。

4)加工误差会引起电枢质量的随机波动[2]。

为了研究静态参数的随机波动对初速的影响，建立全系统的仿真模型，采用蒙特卡罗法来分析电磁轨道炮中放电电压、电容器的电容量、系统电阻、系统电感和电枢质量这5个静态参量的随机变化对电枢初速的影响。

2 电磁轨道炮内弹道随机过程模拟

2.1 蒙特卡洛分析方法

蒙特卡罗方法亦称为随机模拟方法，也称作随机抽样技术或统计试验方法。基本思路是建立一个概率模型或随机过程，通过对模型或过程的抽样试验来计算所求参数的统计特征，给出所求解的近似值，而解的精确度可用估计值的标准误差来表示。

基于蒙特卡洛法的电磁轨道炮随机模拟基本步骤如下：

1)建立所要分析的电磁轨道炮内弹道数值模型。

2)确定发射过程中要研究的随机变量的波动及其分布规律。

3)将随机变量(放电电压、电容器的电容量、系统电阻、系统电感、电枢质量)的抽样值代入内弹道数值模型，进行求解，得到电枢加速度、电容器电压和放电电流曲线。

4)对模拟结果进行统计分析。

2.2 电磁轨道炮内弹道数学模型

2.2.1 电磁轨道炮内弹道过程分析

电磁轨道炮的电路模型如图2所示。

设简单电磁轨道炮导轨宽度为W,则进入导轨的线电流密度i=I/W。设轨道间距为h，当电枢位置在x时，回路电流在两导轨之间形成的磁场截面为hx，磁场强度H指向z负方向。按照麦克斯韦电磁方程：

(1)

式中：j为面电流密度；D为电位移矢量。

(2)

电感储存的磁能：

Wm(I,x)=LI2/2

(3)

磁能随x变化的梯度即为作用在电枢上的洛伦兹力,为[3]

(4)

于是：

(5)

FM为洛伦兹力，当电枢前有弹丸时，弹丸将被电枢驱动而加速，到达轨道末端时发射出去。由式(5)可知，磁场力与电流强度的平方成正比。因此，增大导轨电流可以大幅度增加弹丸初速。

电磁轨道炮在发射时，电枢在电磁力的驱动下沿导轨运动，若不计各种阻力，则运动方程为

(6)

式中：ma为电枢质量；v为电枢速度。

随着电枢的运动，回路电阻、回路电感线性增大，即

R=R0+R′x

(7)

L=L0+L′x

(8)

(9)

式中：Ipeak为脉冲电源放电电流峰值;Lt为系统电感，即电枢运动到发射器轨道终点时的回路电感；U为放电电压。

当t≤tpeak时，

i(t)=Ipeaksinωt

(10)

当t>tpeak时，

(11)

式中,Rt为系统电阻，即电枢运动到轨道终点时的回路电阻[4]。

考虑摩擦力的电枢初速vout的表达式为

(12)

其中，摩擦阻力Ffri的表达式为

Ffri=μFN

(13)

式中：μ为摩擦系数，速度低时滑动摩擦系数取0.3，随着速度的增加摩擦系数下降很快，取值0.1;FN为电枢对轨道的压力。

2.2.2 仿真流程

基于MATLAB软件建立了电磁轨道炮的内弹道模型，进行初速精度蒙特卡罗仿真，软件流程如图3所示。

3 仿真结果分析

3.1 电磁轨道炮内弹道仿真

在MATLAB仿真中，系统电源由6个模块组成，单模块放电电压U为4 kV，电容量C为2 500 μF，电枢质量ma为10 g，系统电感Lt和系统电阻Rt分别为11 μH和9 mΩ。电感梯度L′为1 μH/m。

图4为发射过程中总放电电流和电枢速度的变化曲线，图5为电枢在膛内运动速度的仿真值和实测值对比曲线，初速实测值与仿真值偏差为2%，原因在于仿真模型中考虑到了电枢的滑动摩擦，以及仿真模型中的脉冲电源和发射器的电参数与实际工况较为接近。

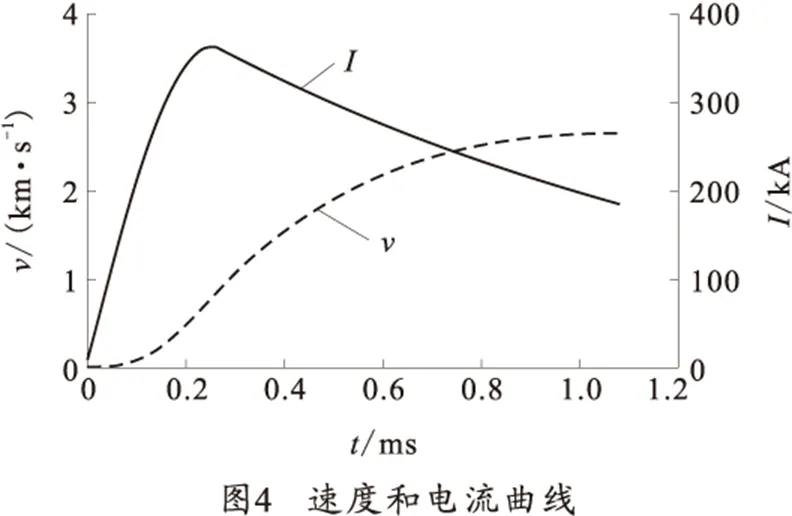
图6为电枢在发射器膛内所受推力和摩擦力的变化曲线，在MATLAB仿真程序中，根据电枢运动速度与摩擦系数的对应关系，确定摩擦系数的取值。电枢的推进力和放电电流在上升沿呈正弦上升趋势，推进力在256 μs时刻达到峰值，峰值为65.83 kN, 在下降沿呈指数衰减趋势。内弹道仿真结果如表1所示。

表1 内弹道仿真结果

参量数值峰值电流/kA361.8剩余电流/kA185.2电枢初速/(km·s-1)2.636发射效率/%28.9

3.2 电磁轨道炮随机过程模拟

采取单因素模拟来分析放电电压、电容、电阻、电感和电枢质量5个随机变量对初速精度的影响。单因素模拟指的是在模拟过程中，只对1个参量随机抽样，该参量服从正态分布，其余的4个参量保持定值不变。按照参量精度依次为1‰,2‰，3‰，4‰，5‰，6‰，7‰和8‰的变化进行单因素随机波动的模拟计算。

参量精度σ的定义为：

(14)

σx定义为：

(15)

(16)

3.3 误差源敏感性分析

根据蒙特卡洛随机模拟数据，将5个参量的精度与初速精度的关系绘制成图，如图7所示。当放电电压、电容器的电容量、系统电感、系统电阻和电枢质量5个参量的随机误差在1‰～8‰范围内波动时，各参量的精度与初速精度近似为线性关系，其中放电电压和电容器的电容量对初速影响最为明显，而系统电感的随机波动对初速精度的影响最小。当轨道电感的精度为8‰时，初速精度仅为3.75‰。各参量对初速的影响水平由高到低为：放电电压、电容量、电枢质量、系统电阻和系统电感。

4 误差分配

如果各误差因素为随机误差，且不相关。则可按照等作用原则分配误差，即：

(17)

如果按照等作用原则进行误差分配以后，导致某个随机因素的精度指标难以实现，则对于难以实现的误差项适当扩大，对容易实现的误差项尽可能缩小，而对其余的误差项不予调整[5]。

采用综合因素模拟的方法进行随机模拟仿真，以此作为误差分配的依据。综合因素模拟是指在模拟仿真的过程中，对所有参量进行随机抽样，所有参量服从正态分布。

在电磁炮内弹道蒙特卡洛仿真模型中，初速精度可视为以参量精度为变量的函数。那么将一组参量精度值代入内弹道仿真模型进行随机模拟，可得到多对参量精度与初速精度的对应数据(即变量扫描)，即可利用最小二乘法对这些仿真数据进行拟合，得到初速精度与参量精度的函数关系式，则可根据初速精度值倒推出参量精度值。再将求解结果回代到内弹道仿真模型中，以验证求解结果是否正确。

4.1 指标平均分配

基于内弹道模型进行电磁轨道炮综合因素模拟。同时对5个参量进行随机抽样，并规定各参量精度相同，则用系统参量精度来描述5个参量的精度。可得到系统参量精度分别为1‰、1.5‰、2‰、2.5‰、3‰、3.5‰、4‰、4.5‰、5‰、5.5‰、6‰、6.5‰、7‰、7.5‰、8‰时对应的初速精度值，共16对数据。然后通过最小二乘法对该16对仿真数据进行拟合[6]，其中系统参量精度为变量，则初速精度为以系统参量精度为变量的函数。经过拟合发现初速精度与系统各参量精度近似为线性关系，函数关系式为

y1=0.006 08+0.98x1

(18)

式中：x1是系统参量精度；y1是电枢初速精度。

根据式(18)，可计算出当初速精度为1%时，对5个参量的精度要求为4‰。再将该分配结果回代到MATLAB内弹道模拟程序进行验证，经过模拟计算得到电枢初速精度0.995‰，可见该分配结果是满足要求的。

4.2 指标不平均分配

在指标平均分配方案中，系统对各参量的精度要求为4‰。由于发射器的加工工艺较为复杂、进行高精度装配存在较大的难度，并且在发射过程中需面临高温、刨蚀、振动等严酷工况，导致系统电阻和系统电感的精度指标难以实现，因此对发射器的误差项适当扩大，脉冲电源、电枢的误差项适当缩小。

根据目前的技术水准，电磁轨道炮各分系统可达到的指标为：脉冲电源放电电压精度为3‰，电容器电容量精度可达2‰，电枢质量加工精度可达2‰。将上述指标代入内弹道仿真模型，则初速精度为以系统电感精度和系统电阻精度为变量的函数。对系统电感精度和系统电阻精度进行变量扫描，两者精度相同，取值范围为4‰～1.4%，步进为2‰。采用最小二乘法对变量扫描结果进行数据拟合，发现初速精度与系统电感精度、系统电阻精度为线性关系，对应函数关系式为

y2=0.038 4x2+0.005

(19)

式中：x2是系统电阻和系统电感精度；y2是电枢初速精度。

进而计算出当初速精度为1%时，系统电感和系统电阻的精度为1.3%。将如表2所示的指标分配方案回代到内弹道蒙特卡洛仿真模型中进行验证，经模拟，初速精度为1.0004%，可见指标分配方案是符合要求的。

表2 指标不平均分配方案

5 结束语

影响电枢初速关键因素包括放电电压、电容器的电容量、系统电感、系统电阻、电枢质量等。为了分析电枢在发射器膛内的运动过程，以及参量的随机波动对初速精度的影响，建立了电磁轨道炮内弹道模型，并采用蒙特卡洛法进行随机模拟。

单因素随机模拟结果表明，脉冲电源的放电电压以及电容器的电容量的随机波动对初速的影响最为明显，而系统电感对初速的影响最为微弱。通过多因素模拟，并综合考虑全系统各部件的的工艺复杂度、实现难易程度、现有技术水平，确定了指标不平均分配方案。

在电磁轨道炮研制过程中，应对各分系统指标进行精确测量和控制，保证各分系统的精度指标符合要求。另外发射过程中发射器与电枢的接触状况、预紧力、轨道面磨损和炮体紧固情况等对电枢的初速也有较为直接的影响，需要借助多物理场仿真、辅助测量工具并结合试验结果进行多次迭代来确定最优设计。