县乡道路网养护修复资金分配的优化分析
2018-10-08苏卫国庄旭青
苏卫国,郭 博,庄旭青
(华南理工大学 土木与交通学院,广东 广州 510640)
0 引 言
目前,中国公路的工作重点逐渐由建设向养护过渡。随着路面待养护里程的逐年增长,养护需求也不断增长,而各市县普遍存在养护资金缺口大、资金使用不合理等问题,因此如何使有限的养护资金发挥最大的经济效益显得尤为重要。资金分配优化要解决的问题就是如何利用有限的养护资金,使其既能满足路网养护需求,又能在此基础上争取资金利用的效益最大化,使区域路网在按计划实施特定养护措施后,路网整体路用性能提高值达到最优,路面处于最佳服务水平。蒋红妍基于理想点和负理想点的多目标最优决策方法研究了高速公路养护资金分配优化问题;王凯利用0-1规划方法研究了高速公路网级路面养护资金分配优化问题[1];杨永红等提出了利用单年度资金分配优化模型解决公路养护资金受限问题[2];徐龙等通过基于粒子群理论建立养护资金分配的优化模型对资金分配进行了研究[3-4]。目前,养护资金分配优化问题的研究对象仍以高速公路为主,对于城市县乡道养护修复资金分配优化问题的研究甚少。
本文对佛山市禅城区县乡道路网路面状况进行全面调查,依托佛山市禅城区县乡道路网养护维修工程,基于养护修复需求,在额定养护资金条件下,利用0-1背包问题模型对县乡道路网级养护资金分配进行优化,确定使整个路网效益得到最大提升的路面养护决策方案,为城市县乡道路网养护修复资金分配优化问题寻找一个解决途径。
1 0-1背包问题模型
1.1 0-1背包问题
0-1规划是整数规划的一种特殊形式,特殊性在于决策变量只取为0或1,同时0-1规划问题又可分为线性、非线性2种,它是组合优化问题的一个重要组成部分。背包问题属于常见的0-1规划问题之一,具体描述为:假设有n个物品,每个物品都会占有一定的体积,同时每个物品都有不同的价值,背包的总体积为V,要求装入背包中的物品的体积之和不能超过背包的体积容量,同时背包内物品的价值总量达到最大[5-6]。引入决策变量xi,用来表示物品i是否被装进背包,如果是则xi取值为1,如果否则xi取值为0,则这一模型如下。

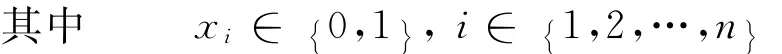
式中:vi为第i个物品占有的资源量;pi为第i个物品的价值。
这是在只有一个约束条件下的背包问题描述,也是一切背包问题的原型。在只有一个约束条件的背包问题中,所有物品都只有一个约束属性,如上述问题中物品的体积属性。若背包问题包含有m(m≥1)个约束条件,则把该背包问题称为m约束背包问题或多维背包问题,多维背包问题中的每个物品都具有多个约束属性,如体积、质量等,决定是否将物品放入背包中的条件更加复杂,多维背包问题模型如下。

式中:Vk为第k种约束条件的约束总量;vki为第i个物品所占有的第k种约束的资源量;其他参数含义和单一约束条件背包问题相同。
本文所研究的路面养护资金分配优化问题中,所要解决的问题是在约束资金条件下,确定路网中的路段是否采取某项修复措施,确定需要采取什么程度、什么类型的养护措施来进行养护。不同路面结构采取不同养护措施所得到的路面性能提升效果是不同的。能最大限度地提升路面性能并获得最大提升值的决策方案就是最佳决策结果。这一决策涉及的约束条件较多,而0-1问题背包模型能够在满足这些约束条件下找到最优的决策方案,所以采取多维约束0-1背包问题模型来进行解决。
1.2 在路面养护资金分配优化中的应用
1.2.1 准备工作
(1)调查路网路面性能。在进行道路路网养护资金分配前,必须先调查整个路网各条道路所处的状态,进而确定各条道路和整个路网的养护修复需求,在此基础上确定路段路面的养护措施类型和需求量[7-8]。措施类型的选择和需求量的确定以及采取措施与否都直接受资金条件的约束。
(2)路用性能组合状态简化。决策问题的规模会直接影响决策问题求解的难易程度,所以为了确保决策问题的可解性,引用了路面性能组合状态的概念[9]。国内现行规范把路面行驶质量指数RQI、路面状况指数PCI、路面抗滑系数SRI、路面强度指数PSSI等4项指标进行了等级划分,划分为优、良、中、次和差5个等级,若所有线路路段路面按照这5个等级进行组合,那么将会出现625种组合,这样庞大的规模将不利于对问题的求解。因此需要对组合状态进行符合工程实际的简化。参考王凯在文献[1]中提出的简化方法,将沥青路面和水泥混凝土路面性能组合状态按实际路况会出现的情况及相应的养护措施类型列出,见表1、2。表1、2中的建议养护措施类型为资金条件允许的情况下采取的养护措施类型,允许养护措施类型为资金条件不允许的情况下采取的措施类型。

表1 沥青路面性能组合状态和养护措施

表2 水泥混凝土路面性能组合状态和养护措施
首先分析路面性能组合状态与养护措施对策的组合情况,沥青路面的使用性能组合状态有11种,对应的路面养护措施有4种;水泥混凝土路面性能组合状态有6种,对应的路面养护措施有4种。将养护措施进行归纳可分为日常养护、预防性养护、中修和大修4类,其中中修措施又可分为中修罩面和中修加铺抗滑层,大修措施可以分为大修补强和大修重建。引入决策变量δki,j表示路网中第k条线路处于第i种路面性能组合状态是否采取第j种养护措施,运用0-1背包问题模型来选择是否采取养护措施,若是则δki,j=1,否则δki,j=0。按照路面性能组合状态与养护措施对策的组合,沥青路面δki,j存在44种组合情况,水泥混凝土路面存在24种组合情况。通过对一些没有意义的对策组合进行筛减,最终沥青路面的δki,j存在22种组合情况,水泥混凝土路面存在11种组合情况。组合情况数量的筛减有利于减小决策规模,也有利于模型的求解。最终沥青路面和水泥路面δki,j的分布如下。
沥青路面

水泥路面

在路面养护活动中,日常养护与小修是一项必要的养护措施,但是这项措施并不能对路面使用性能起到提升的作用(采取日常养护与小修PQI提升值为0)[10-12],它只能保持路面使用性能水平或减缓路面使用性能的衰减。不同养护修复措施类型预计效果、不同性能组合状态的路段采取不同的养护对策措施所得到的养护提升效果是不一样的,具体见表3。为了能够定量描述养护效果的提升值,引入变量Ci,j,其含义是处于第i种路面性能组合状态的路段采取第j种养护措施后PQI的提升值。

表3 不同组合状态路段采取不同措施PQI提升值
1.2.2 养护资金分配优化
以区域路网采取养护措施后PQI的提升值来反映养护措施效果和所获得的资金效益,为了减小决策规模且便于模型的最终求解,这里只进行单一年份的养护资金的优化。已经确定了路面养护的预算资金,资金优化就是要在这一约束资金条件下合理地安排路面养护措施方案,以获得最大的路面性能提升值,0-1背包模型应用于养护资金分配优化具体描述如下

式中:α为目标函数,即采取养护措施方案后路网的PQI提升值;βk为第k条线路的重要度系数;Bt为第t年路面养护约束资金,实际工作中受地方财政实际水平限制,也可以根据各地方养护资金的实际水平确定;Lk为路网中第k条线路的里程(km);Dk,i为路网中第k条线路处于第i种路面性能组合状态所占的比例;γk,j为第k条线路采取第j种养护措施每公里所需的费用(万元);Ci,j为处于第i种性能组合状态的路段采取第j种养护措施所提升的PQI值;s.t.为约束条件。
约束条件第1项对决策变量的取值范围进行了约束,δki,j只能取值0或1,为0-1背包问题模型的决策依据;约束条件第2项表示处于某一组合状态的路段采取的养护措施种类不能多于一种;约束条件第3项表示进行路面养护资金分配优化必须在约束资金条件下进行;约束条件第4~11项对有意义的路面性能组合状态与对应的养护措施进行了约束,确保处于某一路面性能组合状态的路段所采取的养护措施在允许范围内,对于路面抗滑性能不足和结构强度不够的路段必须采取强制措施。
2 应用实例
2.1县道路网状况
佛山市共辖5个区,包括禅城、南海、顺德、三水、高明,县道总里程约650km,每年各区县道路面养护资金都由市、区财政拨款,每年的路面养护资金基本一致,但是各区域资金水平不同,同时每个区域的养护资金只能在该区域使用。本文以佛山市禅城区的12条县乡道组成的路网(共65.944km)作为研究对象,进行路面养护资金分配优化,12条县乡道基本概况如表4所示。
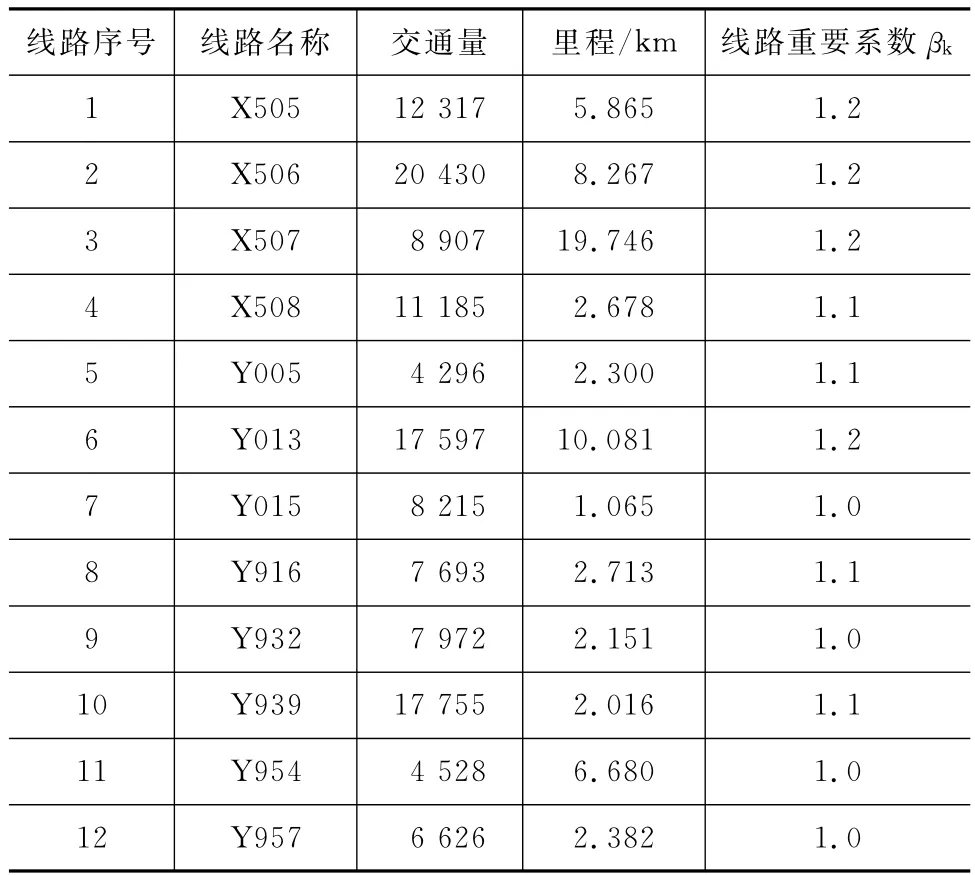
表4 佛山市禅城区县乡道概况
2017年作为本文对佛山市禅城区县道路网的研究基年,在2017年路况调查检测数据的基础上进行路面性能评价、养护需求分析、养护资金分配优化及最后方案的制定。依据2017年调查资料对佛山市禅城区进行路面养护需求分析,佛山市禅城区县道路网路面性能组合状态根据上文提到的方法按表1、2进行简化归纳。调查计算结果如表5所示。
表5中数值表示的是线路中某一路面性能组合状态路段里程和该条线路总里程的比值。
根据各条线路路面性能组合状态的分布情况,可以得到2017年禅城区路面养护的实际需求,所有需求都按照表1和表2中的建议养护措施来实施,可得到各路段的养护需求量。汇总结果如表6所示。

表5 不同路面性能组合状态的占比
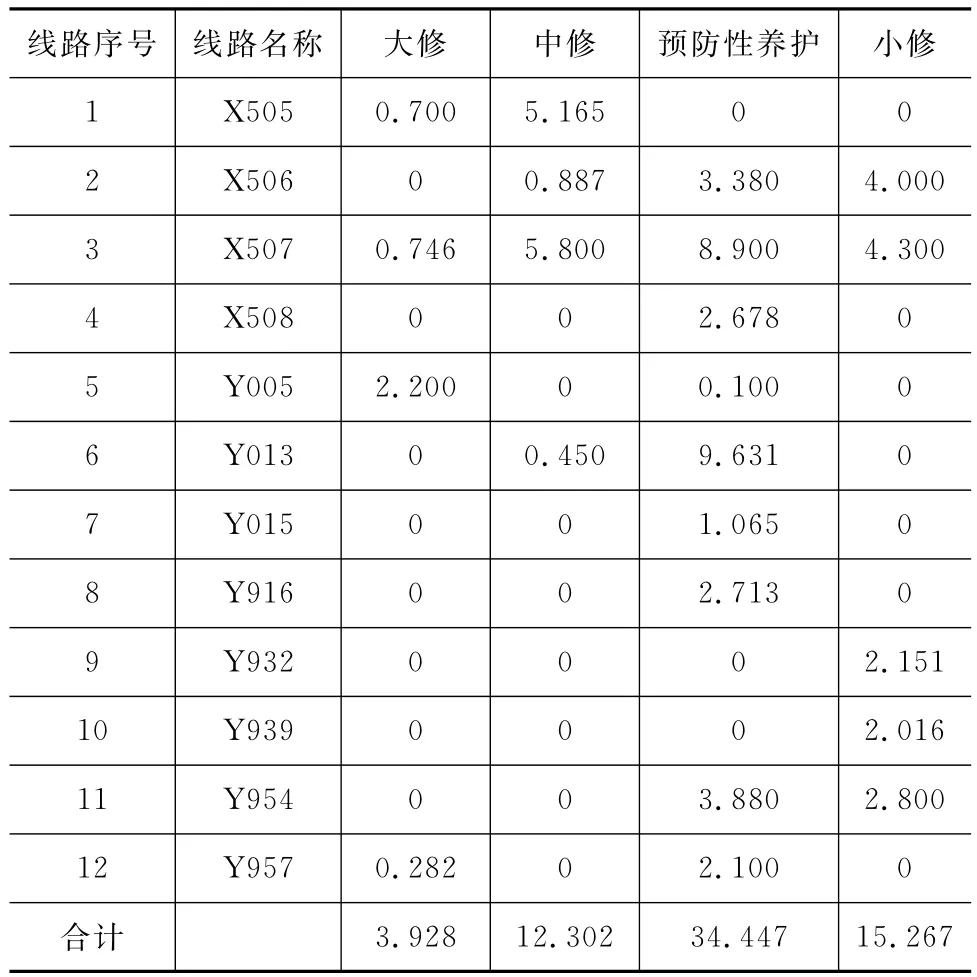
表6 2017年禅城区路面养护需求 km
从表6可以看出:县乡道路网路面总体性能较好,需采取日常养护与小修的路段有15.267km,占研究对象总里程的23.2%;需要采取预防性养护措施的路段有34.447km,占研究对象总里程的52.2%;需要采取中修措施的路段有12.302km,占研究对象总里程的18.7%;需要采取大修重建养护措施的路段有3.928km,占研究对象总里程的5.9%。若按表6的养护需求进行2017年的县乡道路网修复,可得到2017年禅城区用于大中修和预防性养护的修复资金总额为4 046.562万元,超出禅城区2017年实际可使用的养护资金2 911.079万元。因此,有必要对其进行养护修复资金分配优化。
2.2 养护决策优化
在进行县道路面养护资金分配优化计算前,还需要确定模型中所有相关参数的取值。不同路段路面宽度不同,不同养护措施的养护费率各不相同,同时中国县乡道路面的养护管理还缺乏统一的养护定额标准。所以,本文结合佛山市禅城区经济水平和各线路历史养护费用,同时参考有关规范进行取值,结果如表7所示。
根据佛山市交通局所给资料,佛山市禅城区每年可用于路面养护修复的固定资金包含两部分:一部分是用于大中修和预防性养护的费用,每年2 911.079万元;另一部分日常养护与小修的资金由区财政单独补助。日常养护与小修并不能对路况进行提升,所以对于日常养护与小修的路段在计算中不予以考虑。在县乡道路面养护资金已经给定了约束值的条件下,运用0-1背包问题模型对县道路面养护决策优化模型进行求解。核心计算过程采用LINGO软件进行编程求解计算。
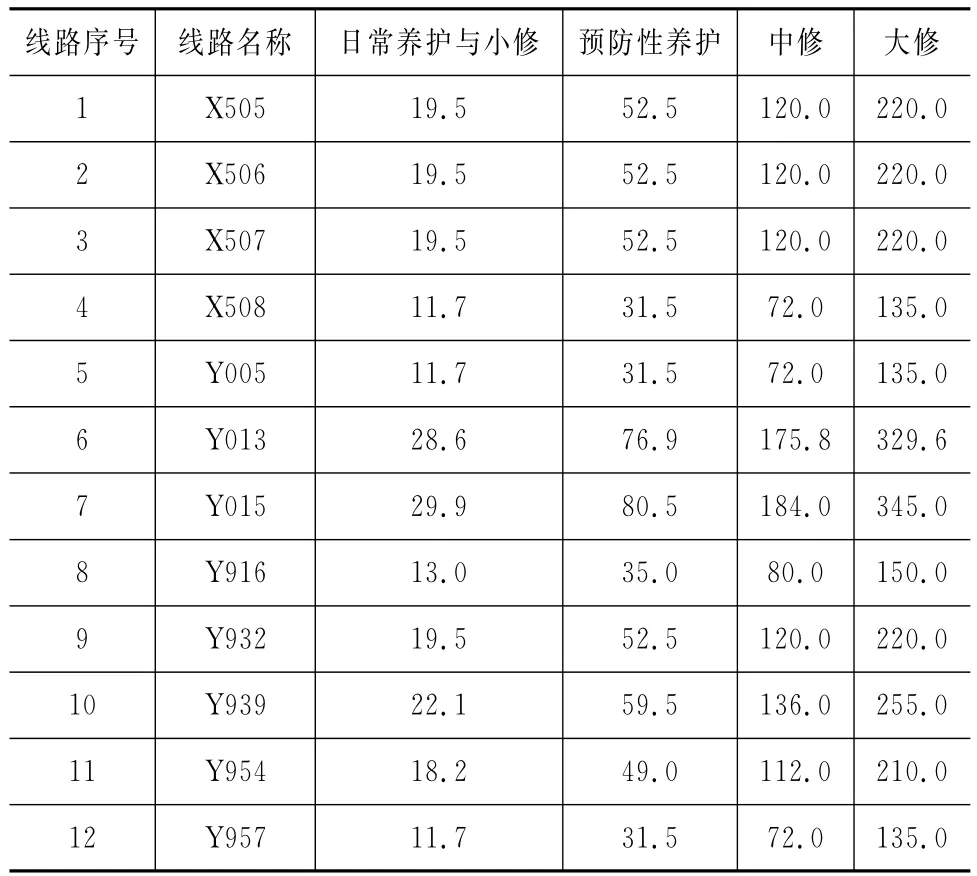
表7 每公里路面养护措施费用取值 万元
采用0-1背包问题模型经LINGO求得:禅城区65.944km县乡道路面采取日常养护与小修措施的路段有34.256km,采取预防性养护措施的路段有15.458km,采取中修措施的路段有12.302km,采取大修养护措施的路段有3.928km。
计算得整个路网PQI提高值为337.006,平均每公里提升5.11,总费用2 896.267万元,小于约束资金2 911.079万元,满足条件。详细养护方案按LINGO计算结果汇总后如表8所示。

表8 佛山市禅城区县乡道路面养护资金分配结果
3 结 语
本文运用基于0-1背包问题的模型对佛山市禅城区的县乡道路网进行网级养护维修规划,得出以下结论。
(1)调查了佛山市禅城区县乡道路网的路面状况和禅城区的养护修复资金来源、组成。对各路段所处的路用性能状态进行简化,使其更贴合实际路况,同时使模型更简单,更易于理解和应用。
(2)以路用性能PQI的提高值最大化为目标,选择0-1背包问题模型为优化途径,很好地解决了如何将县乡道路网有限的养护资金合理分配,实现效益最大化的问题。
(3)本文以佛山市禅城区县乡道网级规划为例,验证了0-1背包问题模型应用于县乡道养护资金分配优化的可行性,证明该方法简单、实用,具有较高的实际应用价值。
