波动加压下旋挖钻机破岩能力的有限元分析
2018-10-08徐信芯韩向青边晓伟史为品
徐信芯,王 锋,韩向青,边晓伟,史为品
(1.长安大学 公路养护装备国家工程实验室,陕西 西安 710064;2.陕西省特种设备检验检测研究院,陕西 西安 710048)
0 引 言
旋挖钻机是一种取土成孔灌注桩施工机械,靠钻杆带动回转斗旋转切削土并将其提升至孔外的周期循环作业装备[1],因钻进效率和准确性高、对环境污染小、成桩质量好和自动化程度高等优点[2],其应用范围已经覆盖施工难度较大的山区、半山区、丘陵等地带,且多数地层中含有较难钻进的坚硬岩石层。然而,单靠加压油缸的加压力很难实现快速入岩,导致施工效率低,钻具磨损大;因此研究高效入岩破碎的方法,对提高施工效率和延长钻具的使用寿命具有重要意义。
各国学者对旋挖钻机的破岩能力进行了研究:如Liu等[3]对压头作用下岩石的变形机理进行了研究,用数值模拟分析单压头和双压头作用下岩石的破碎过程;李国华等[4]研究了静载、动载单独和联合作用下破岩的异同点和相互关系,并证明了2种载荷联合作用可以提高硬地层的钻进效率;赵伏军等[5]对花岗岩在静载、动载和动静组合载荷作用下的破坏过程进行了数值模拟分析,证明了动静组合载荷破岩能力比静力压入或单一冲击更具有优势,能提高破岩效果;Petersen等[6]研究了在动静载荷作用下混凝土和花岗岩材料的破坏机理;谢世勇等[7]在动静态多功能岩石破碎实验台上,以花岗岩为试验对象分别对单一静载、冲击载荷和动静组合载荷破岩进行了研究;左宇军[8]对动静载荷组合加载下岩石破坏的特性进行了研究,尤其是对一维和二维动静组合加载理论与试验进行了深入系统的研究;葛修润等[9]则对循环荷载作用下岩石的变形与疲劳破坏展开了系统的研究工作,并利用力学和细观CT扫描试验做了相应验证。
以上的研究多数是针对动力头不同载荷形式破岩效果对比进行的,对于动力头具体的加压方式等方面的研究较少[10-12]。本文基于钻具切削岩石的破岩机理,提出动力头波动加压的入岩钻进方法,采用有限元法建立单齿破碎岩石的过程动力学模型,仿真分析波动压力下岩石的应力、应变和裂纹情况,通过对比静载作用和低频循环动荷作用下岩石破碎的效果,验证动力头波动加压施工的优越性。
1 钻具钻进硬岩的模型建立
在Pro/E中建立钻齿、岩石相接触的三维实体装配体模型,选用短螺旋钻具,齿数为12,锥角为80°,最大直径为1 000mm。本文主要研究短螺旋钻具最底部先接触并钻进岩石的过程,故建立钻具芯轴顶端一个钻齿与岩石接触的实体模型,如图1所示。
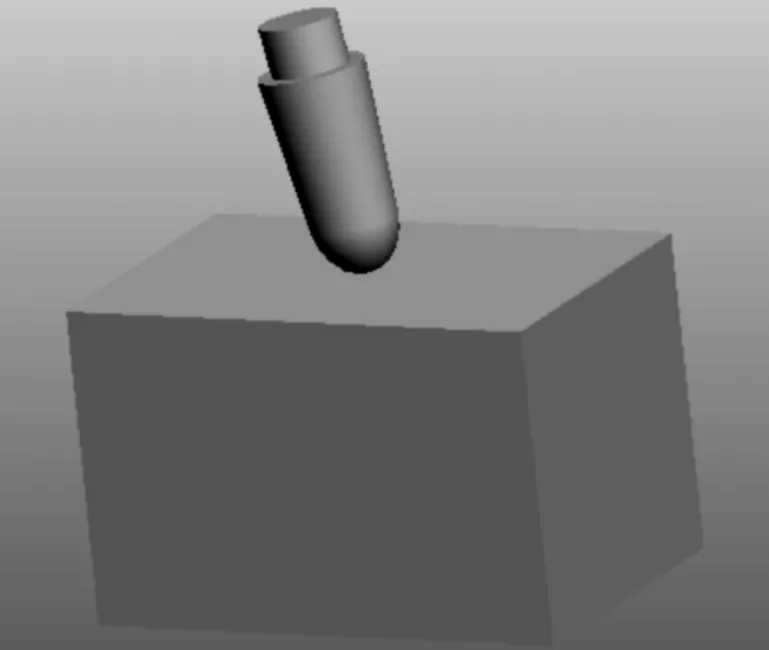
图1 截齿与岩石接触模型
岩石选用花岗岩模型,尺寸为100mm×70mm×70mm。钻齿采用SOLID45单元模拟,花岗岩采用SOLID65单元模拟。温度对岩石强度参数产生的影响较小,故忽略不计[13]。钻具和岩石的具体材料参数见表1、2。为了避免应力集中的出现,网格采用六面体划分,共61 250个单元,网格划分后的模型见图2。
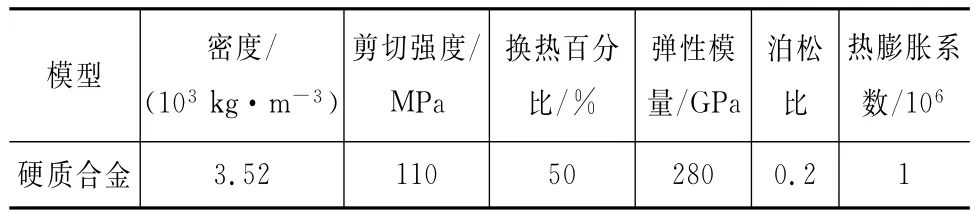
表1 钻具的材料参数
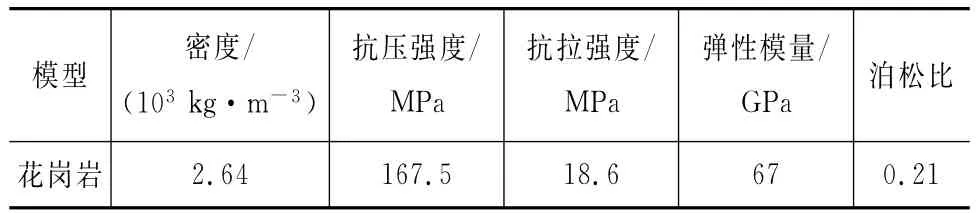
表2 岩石的材料参数

图2 网格划分模型
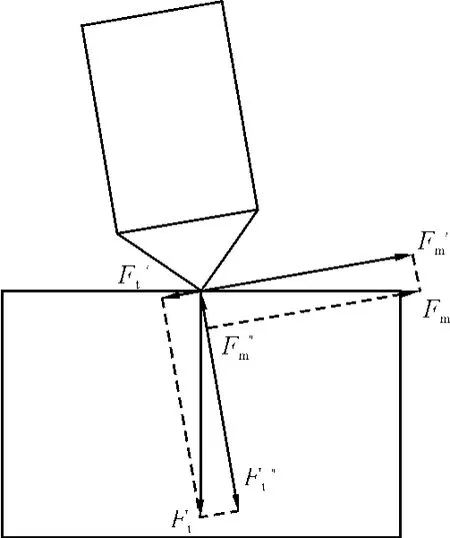
图3 模型施加力示意
2 静载作用下岩石破碎的仿真分析
旋挖钻机在实际施工时,加压油缸提供沿钻杆的轴向压力Ft,动力头输出使钻具旋转的转矩M。现将力简化到截齿与岩石接触的点上,如图3所示。将轴向的加压力Ft分解为垂直截齿的分力F′t和沿倾斜截齿方向的分力F″t;将钻具所受的扭矩转化为截齿顶端的水平力Fm,并分解为垂直截齿的分力F′m和沿倾斜截齿方向的分力F″m。对模型的接触点施加的力即为沿截齿方向的2个分力的合力(F″t+)。本模型主要研究轴向加载的破岩效果,选取固定的扭矩,即固定的水平力
由于仅考虑施加的单轴静载荷,且仅有截齿的进给行为,故将岩石模型的底面施加全位移约束,模型前后左右4个面为自由面,保证钻齿的纵向进给。静载荷直接施加在截齿与岩面相接触的节点上,方向为沿钻齿的纵向。
为了分析在单轴静载荷作用下模型的应力、应变和裂纹扩展随子载荷变化的情况,分别对模型施加932N、10kN、20kN、30kN、40kN和60kN的静载荷,选取破碎效果较明显的阶梯性载荷计算最终收敛结果并进行分析。
图4为不同静载荷产生的单元节点裂纹分布,图中裂纹面上的圆圈线表示单元存在裂纹,裂纹面上的八面体表示单元破碎,裂纹面上的圆圈线加“X”表示裂纹先张开后闭合。
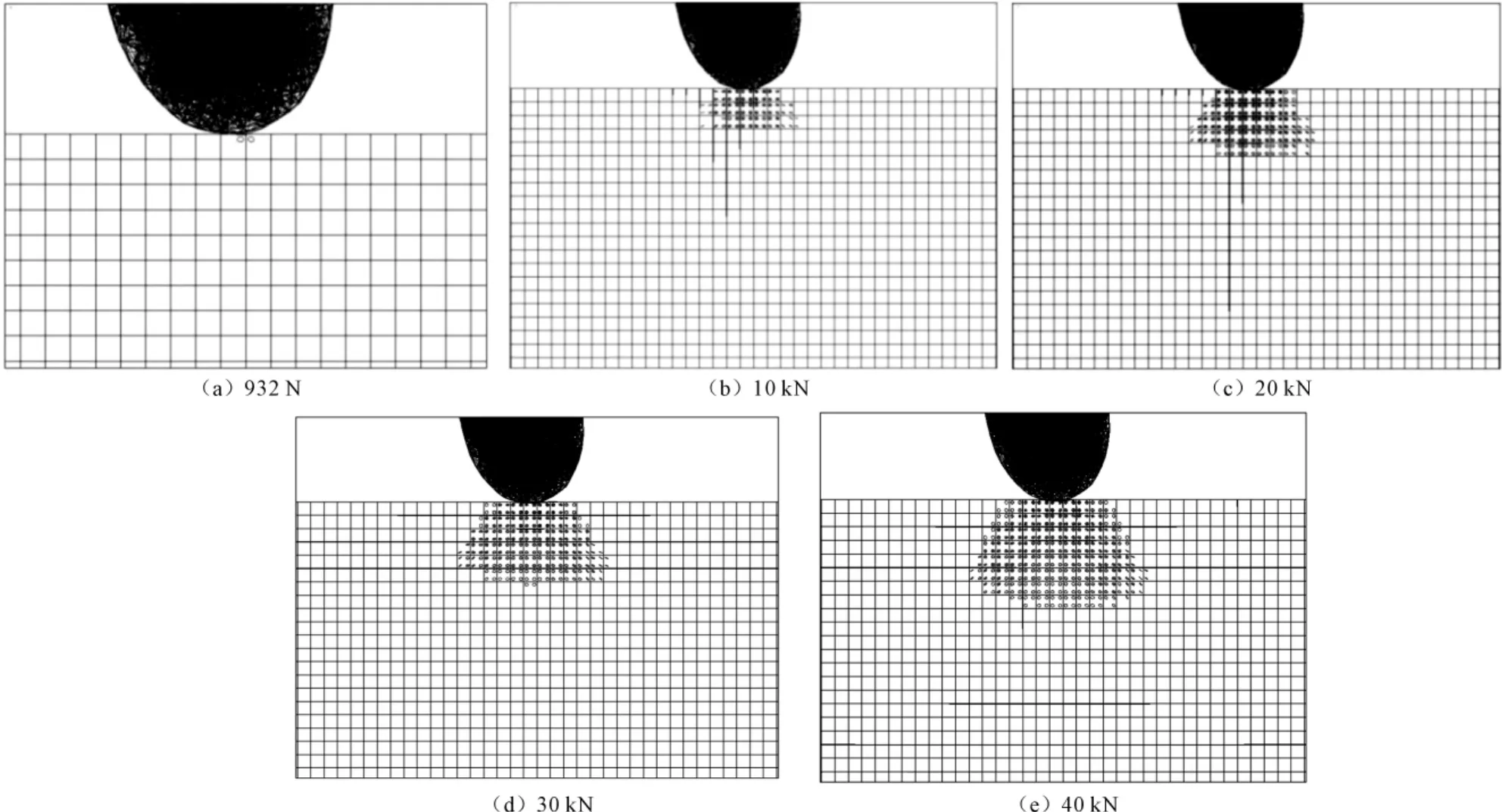
图4 不同静载荷的单元节点裂纹分布
图5为静载作用的岩石破裂深度曲线,当载荷低于932N时,岩石处于弹性和塑性变形期,应力不足以使岩石产生裂纹;施加载荷为932N时,应力区出现在刀具与岩面接触点的下方及相邻2个节点处,裂纹将先在刀具和岩面接触点的下方出现,但分布面极小(图4)。在静载压力小于30kN的阶段,岩石垂直方向的裂纹扩展速率较快,30kN时裂纹深度达到14mm;当静载压力超过30kN时,岩石垂直方向的裂纹扩展速率趋于平缓。水平方向的裂纹在10kN时扩展到8mm。随着静载荷的增加,裂纹扩展速率明显降低,在静载压力为60kN时裂纹深度达到16mm。随着静载压力的增加,岩石裂纹的扩展趋势逐渐减缓,所以如果只单纯地提高静压力,会使破碎深度增加缓慢,破岩效果不显著。
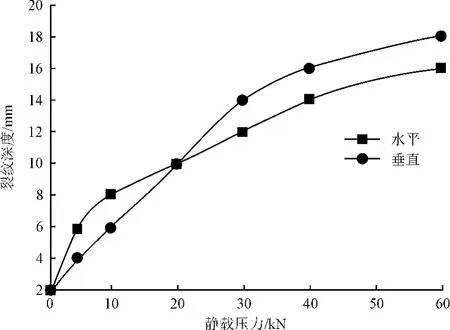
图5 静载破岩深度曲线
3 低频循环动载荷作用的仿真分析
3.1 低频斜坡载荷作用
斜坡载荷在4s内由0增加至40kN,斜率为10kN·s-1,采用瞬态法求解。斜坡载荷下岩石破碎曲线如图6所示,载荷36kN和40kN的裂纹分布如图7所示。
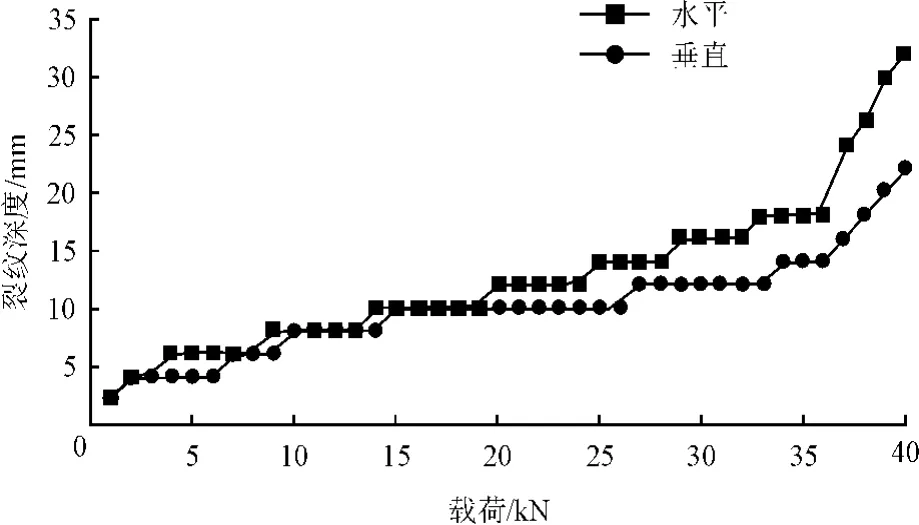
图6 裂纹深度曲线
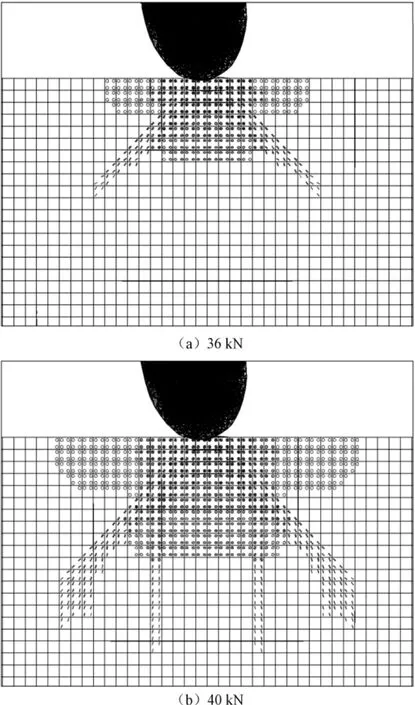
图7 斜坡加载时裂纹分布
由图6可知:在载荷峰值未达到36kN时,随着载荷的增加,岩石裂纹以较低的速率扩展,其中裂纹在水平方向扩展较快,垂直扩展相对较慢;当载荷压力超过36kN时,水平和垂直方向的裂纹扩展速率明显加快,水平扩展增幅明显。将36kN定为该模型的破碎门槛载荷值,并以此为参照对正弦、方波载荷进行仿真,进一步验证了岩石破碎效果不是随载荷的增加而均匀变化,而是当载荷压力达到临界值后突然侵入破碎。
3.2 低频方波载荷作用
加载方波函数需要用表数组来定义。定义一个方波函数,各时间点的载荷如表3所示。

表3 时间点的载荷对应关系
从t1到t2为方波函数,定义一个6行2列的表数组,如表4所示。

表4 加载数据
数组的行、列号都是从0开始,第0列用来存放时间点,第一列用来存放载荷值,dt是一个很小的值,用于使载荷在0和L1之间过渡。使用瞬态求解,方波载荷下岩石破碎曲线如图8所示。载荷36 kN和40kN的裂纹分布如图9所示。
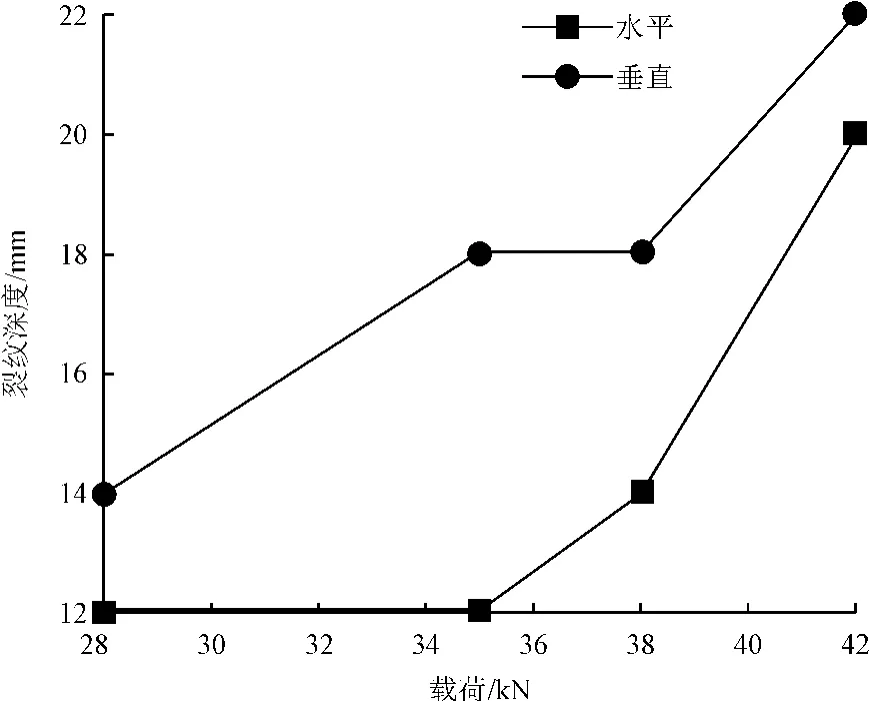
图8 裂纹深度曲线
方波加载时,载荷的施加和撤销较快,每半个周期中力的变化速率为零,即保持力不变。半个周期结束瞬间跳转为另一个荷载,并保持不变。从图8、9可知,幅值载荷36kN为裂纹发展的拐点,载荷幅值由36kN增加到40kN,裂纹在2个方向都有一定的增加,但是增幅较小,裂纹集中在截齿接触岩石的下方,呈锥形分布,未出现劈裂现象。
3.3 低频正弦波载荷作用
正弦波加载方式的特点是:每个周期中力的加载速率不断变化,而不同周期相同位置上的力的加载速率相同,每个周期中的波峰、波谷处于加载速率较慢处,尤其在转折点上停留时间相对较长,使得蠕变效应增大。周期载荷影响岩石破坏的因素有很多,如循环载荷的峰值、幅值、频率、波形等,本模型中加载波形的频率为0.25Hz,主要研究加载峰值对岩石破坏的影响。
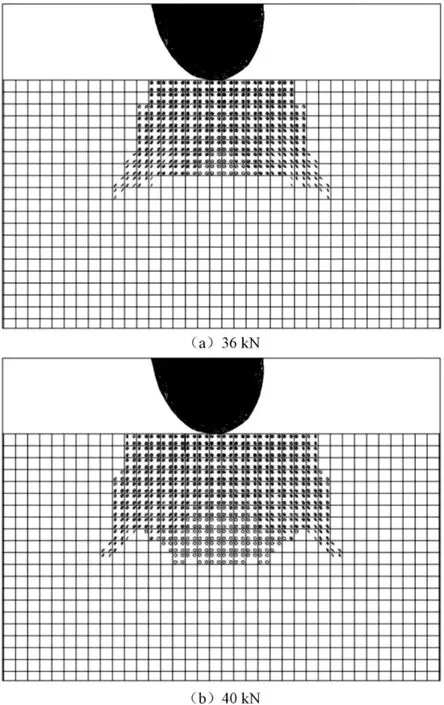
图9 方波载荷的单元节点裂纹分布
正弦波形载荷的周期为4s,最小载荷为0,选取不同的载荷幅值进行仿真计算,使用生死单元法对仿真结果进行后处理。正弦载荷下岩石破碎曲线如图10所示。载荷36kN和40kN的裂纹分布如图11所示。
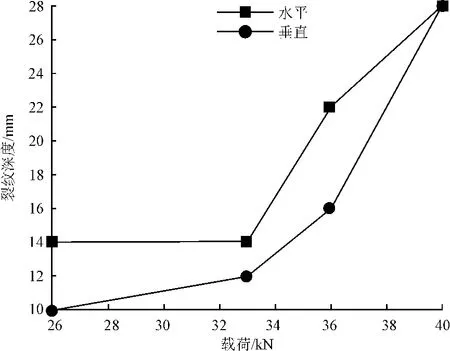
图10 裂纹深度曲线
由图10、11可知,正弦波载荷下水平和垂直方向的裂纹发展都呈增长趋势,幅值载荷越过36kN时,水平方向裂纹发展迅速,裂纹分布密度增大。水平和垂直方向的裂纹长度和破碎面积都大幅度增加,网格破碎效果显著,并在垂直方向出现劈裂现象。
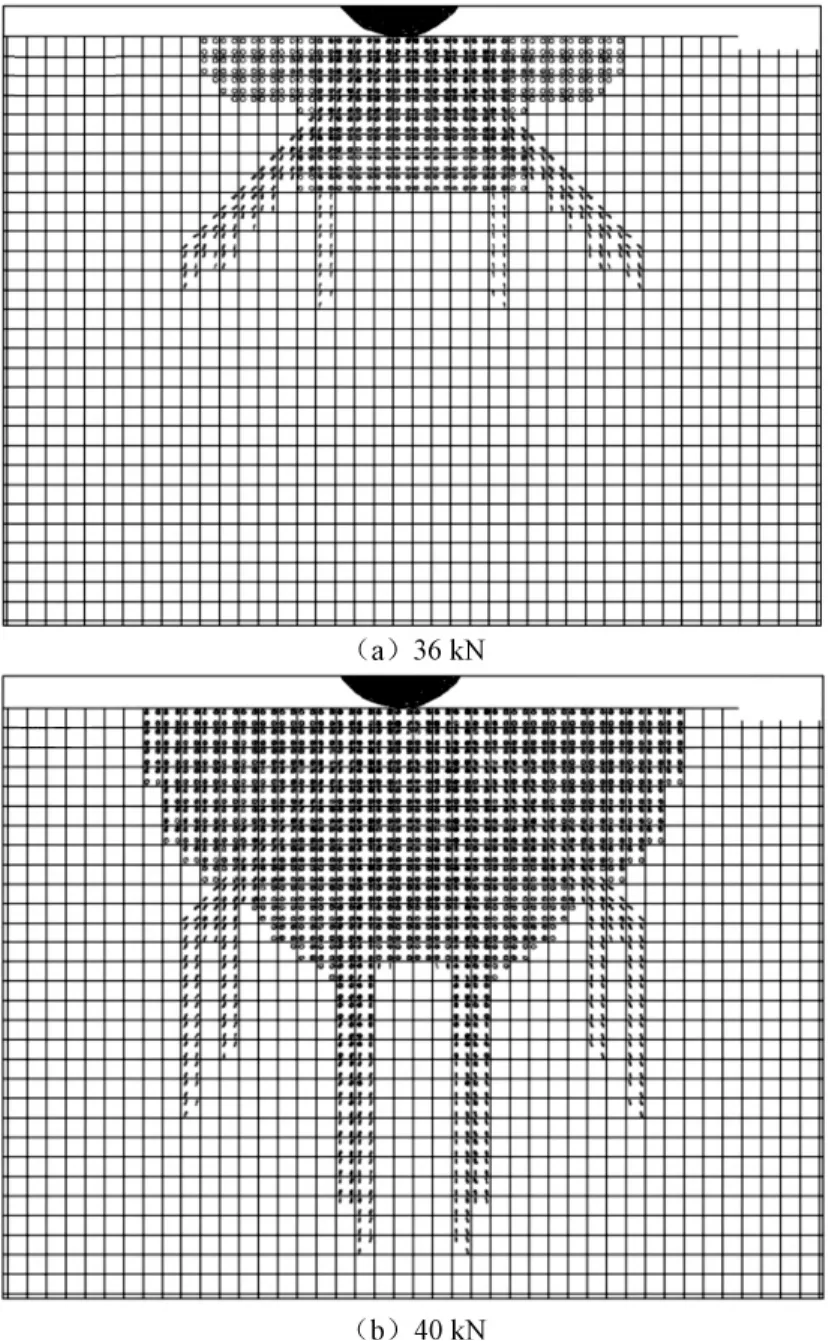
图11 正弦载荷的单元节点裂纹分布
岩石裂纹同时具有方向和大小因素,符合矢量定义,用裂纹综合指标S表示岩石的水平、垂直发展方向的裂纹,如式(1)所示。S值越大,表明裂纹扩展效果越好,岩石破碎程度越大。

式中:X为水平方向裂纹长度(mm);Y为垂直方向裂纹长度(mm)。
对比不同波形动载下综合破岩指标S曲线(图12)可知,随着峰值载荷的增加,3种加载方式的裂纹均扩展,但对岩石造成的破坏效果不同。载荷从26kN增大到33kN,方波和正弦波的S曲线斜率相仿,但方波造成的岩破裂深度大于正弦波和斜坡;载荷从33kN增大到36kN,方波和斜坡的S曲线相同,正弦载荷的岩石裂纹发展速率明显高于方波和斜坡载荷。超过门槛值(36kN),S曲线斜率从大到小依次是斜坡、正弦、方波载荷。在40kN时正弦载荷S值最大,岩石破碎效果比方波和正弦载荷好。
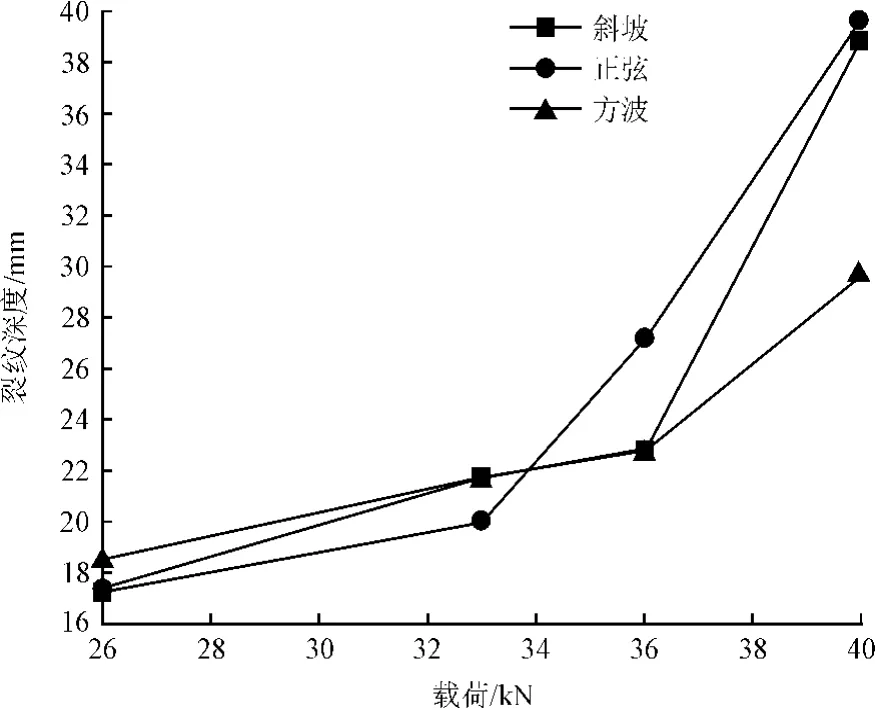
图12 不同波形动载下的综合破岩曲线
4 结 语
(1)随着静载压力的不断增加,岩石裂纹深度增大,但扩展速率逐渐减缓,所以仅单纯地提高静压力,会使破碎深度增加缓慢,破岩效果不显著,破岩效率低。
(2)斜坡和方波载荷加载过程中,随着载荷的不断增加,岩石裂纹深度增大,当施加载荷超过36kN时,岩石破裂速度显著增大,即将36kN定义为岩石破碎门槛值。正弦波形加载时,36kN也是正弦波形载荷的破碎门槛值,在载荷超过36kN时,岩石加速破碎,并在连续的载荷作用下出现劈裂现象。
(3)对比静载和低周期循环动载荷发现,低周期循环动载荷有更好的破岩效果,峰值连续超过破碎门槛值的周期波形能促进裂纹的快速发展,尤其是持续的波动载荷加载更能促进水平方向裂纹的扩展,峰值的大小则主要影响岩石垂直方向上的裂纹扩展深度。
(4)对比斜坡、方波和正弦载荷发现,当施加载荷超过33kN时,正弦载荷的岩石裂纹速率明显高于方波和斜坡载荷,且正弦载荷的岩石破碎深度相对较大。
