超越不等式的解法探究

□海南省海南师范大学数学与统计学院 林瑞记 郑伊楠

一、引言

不等式的求解本身是训练和考察学生数学思维的重要素材，更能体现数学学科的核心素养。所以，不等式的研究工作一直以来都是非常活跃，不仅研究成果如雨后春笋，而且不等式的各个分枝也都是具有强大的吸引力的研究领域。不等式的解法有很多种，如：比较法、综合分析法、反证法、放缩法、数学归纳法、换元法、抛物线技巧法、几何证明法、积分法、极值法等等。然而，有关求解超越不等式的数学分析方法，依旧缺乏系统理论层面的提升。本文按照指数类不等式、对数类不等式、三角类不等式分类来求解或者证明，再由特殊的解法归纳总结到一般的解法。

二、关于指数类超越不等式的解法探究

对于指数类超越不等式，利用已有的基础知识来求解。比如解一般指数不等式的同底法，即将超越不等式的指数式化为同底的指数式，然后利用指数函数的单调性求解。

解：原超越不等式可化为

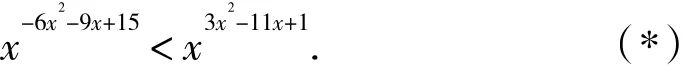
（1） 当0＜x＜1时，（*） 式则同解于不等式-6x2-9x+15＞3x2-11x+1.即 ：9x2-2x-14＜0.由 于9x2-2x-14=0的两个根分别为得9x2-2x-14＜0的解集为以，当0＜x＜1时，可以求得原超越不等式的解集为0＜x＜1.

（2） 当 x＞1时 ，（*） 式 则 同 解 于 不 等 式-6x2-9x+15＜3x2-11x+1，即：9x2-2x-14＞0，它的解集为以当x＞1时，原超越不等式的解为

三、关于对数类超越不等式的解法探究

类比于上例的讲解，对于对数类的超越不等式，也可以将超越不等式的对数式化为同底的对数式，然后利用对数函数y=logax的单调性求解。

解：原超越不等式可以化为

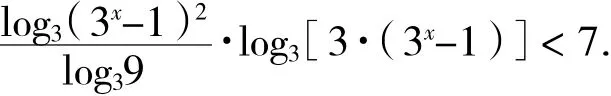
即

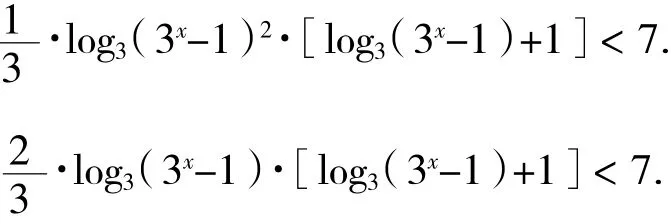
令y=log3（3x-1）·则有，即：y2+y-＜0.解y2+y-=0的两个根分别为y1=-

所以有

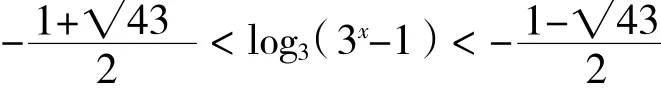
即

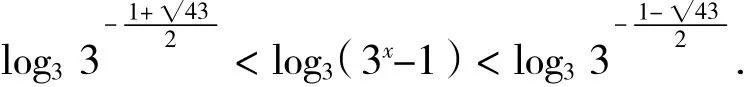
提问是大多数初中英语阅读课堂的必有环节之一，不仅可以激发学生学习英语的好奇心，也可以锻炼学生的分析能力以及解决能力，更可以活跃课堂气氛。英语老师可以在综合评估学生英语知识水平的基础上对不同层次的学生设置不同的问题，加强英语阅读课堂提问与学生知识水平的贴合度。

故

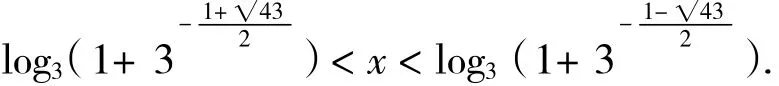
所以，原不等式的解集为log3

例3：解不等式log36

解：设x=log36t，则可得到.故原不等式可化为log7（1+6x）＞x，可得7x＜1+6x.两边同除7x以又可得到，令，则g（x）在x∈R上是减函数，且有，所以＞1，当且仅当x＜1.从而x=log36t＜1.所以，原不等式的解集为｛t｜0＜t＜36｝.

四、关于三角类超越不等式的解法探究

对于三角类的超越不等式，利用已有的三角函数知识来解答。比如：利用三角函数的恒等变化，以及三角函数的单调性、正负区间等特性来解决。

例4：设x∈（0，2π），n为正整数，解超越不等式sin

解：原不等式化为

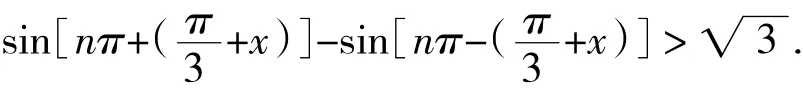
再利用和差化积公式，可得

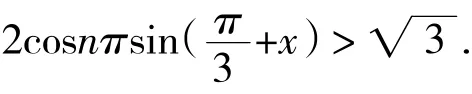
故原不等式的解为：

当n为奇数时，原不等式的解为π＜x＜2π.

结语

通过以上例子，归纳超越不等式的求解步骤如下：

（1）对超越不等式先做适当的变化；

（2）把不等式所有关联的项移到一边，令其为函数h（x）；

（3）确定h（x）的定义域；

（4）令函数h（x），解其超越方程；

（5）进一步讨论函数h（x）在各个区间上的符号；

（6）由函数h（x）在各个区间上的符号，确定原不等式的解集。