基于最小Spanning树的中继节点部署算法*
2018-09-27沈俊鑫南金秀张经阳
沈俊鑫, 南金秀, 张经阳
(1.昆明理工大学 管理与经济学院,云南 昆明 650093; 2.钦州学院 经济管理学院,广西 钦州 535001)
0 引 言
随着环保概念日益深入,绿色通信已受到广泛关注。从环境资源采集能量成为解决无线传感器网络(wireless sensor networks,WSNs)[1,2]的能量受限问题的有效方案,如电磁波、太阳能、风能等[3,4]。因此,在WSNs中补充具有能量采集的中继节点(relay nodes,RNs),进而弥补能量消耗殆尽的节点在WSNs空缺,提高网络覆盖率,目的是确保网络连通率,并使RNs数目最小,降低成本。本文考虑了周期性数据流,即每个节点周期向基站传输数据流。同时,节点具有绿色能量采集能力。由于节点自身硬件、位置的不同,其能量采集率不同。
本文针对能量采集率不同的节点,提出了基于最小Spanning树的中继节点部署算法(minimum spanning tree-based deploying relay nodes,MST-DRN)算法,其目的在于以最少的RNs数,满足网络连通率,并保证数据传输成功率。MST-DRN算法基于节点的能量采集容量,计算每个节点的权值,再计算边权值,然后依据边权值,并利用Kruskal算法构成最小Spanning树(minimum spanning tree,MST)。最后,检测MST的非叶节点的能量是否满足数据流的传输要求:若不满足,则成为低能量节点(nodes with low energy capacity,Ns-LEC)。Ns-LEC需要RNs的协助,从而保证网络连通。实验数据表明:提出的MST-DRN算法能够以最小的RNs节点维持网络连通,降低了成本,也提高了数据包的传输成功率。
1 网络模型及约束条件
1.1 网络模型
考虑无向图G=(V,E),V表示顶点集,E表示边。假定链路双向,如果两节点在彼此通信范围内,则这两个节点存在一条边。因此,假定图G=(V,E)连通[5]。
此外,考虑周期流量,即每个节点周期向基站发送感测数据。假定每个节点的感测数据的格式是预知的。同时,假定赋予节点不同能量采集容量。同时,保证最小容量值也足够大,能够维持一个节点运行感测任务和处理自身流量的能量。同时,假定传感节点已部署于感测区域,网络拓扑图,并作为模型的输入。在感测区域内部署RNs节点最终提高Ns-LEC能够转发数据流。为此,将RNs放置于Ns-LEC的临近区域,辅助转发数据包。
1.2 数据流量模型
每个传感节点周期向基站传输其所感测的数据。假定γi表示节点i的支叶节点数,即节点i是根节点,而γi为子节点数和孙子节点。引用Ci表示直系子节点数[6,7]。
每轮抽样时期T,节点产生λbit数据。因此,传感节点(假定节点i)所能接收的数据流为
(1)
节点i将传输的数据流为Tri=λ(γi+1)。
1.3 能量模型
考虑无存储的简单能量模型,即本周期所采集的能量立即在下一个周期使用。假定hi是节点i的能量采集率。不同节点具有不同的能量采集率。设有不同的能量资源[8,9],如太阳能、风能。但太阳能是不可控能量,无太阳照射的区域,节点无法收集能量,就无法保证网络连通,降低网络性能。为此,引用可控能量,即考虑无线能量采集系统。每个节点通过从基站(base station,BS)的无线信号进行充电。文献[10,11]已证实了无线功率传输的可操作性。同时,BS引用Beamforming技术形成尖利能量束,并传递至能量采集节点,利于能量转换效率。
此外,基站采用不同于数据传输带宽的带宽传输能量。如果能量传输和数据传输的带宽相同,可能会产生干扰。
假定节点i所采集的能量表示为Ehi,其定义为
Ehi=ηhiPt(di)-βξiT
(2)
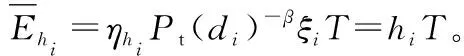
令Ep为在每一周期内执行感测、计算任务时所消耗的能量,Et,Er分别为传输或接收1 bit所消耗的能量,节点i所消耗的总能量Ei=ReciEr+TriEt+Ep。
因此,节点生存条件就是:所消耗的能量小于所采集的能量,即hiT≥Ei,∀i∈S。
2 MST-DRN算法
MST-DRN算法依据边权值构建Spanning树后。计算树的非叶节点是否满足节点生存条件:如果不满足,在其附近部署RNs节点。即通过最小Spanning树寻找Ns-LEC,实现既保证网络连通,又使Ns-LEC的数目最小化。整个流程如图1所示。

图1 MST-DRN模型的执行流程
2.1 节点权值和边权值
通过VWG便可产生边权值图(edge weighted graph,EWG)。每条边权值等于两顶点权值和,即Wu,v=wu+wv,如图2,节点5的能量采集容量h5=20,经计算可知,hmax=30,节点5的树值w5=0.33。由图3计算知,节点5,9的边权值为0.49(即0.33+0.16)。
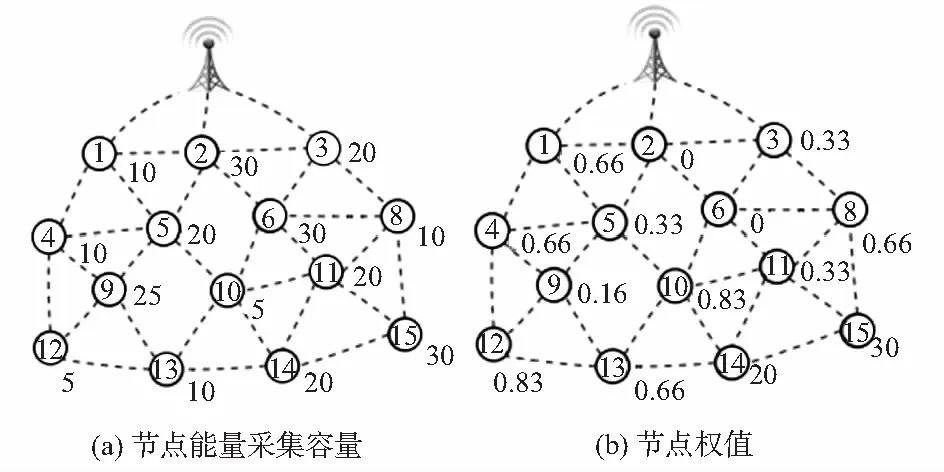
图2 具有节点权值的网络拓扑图
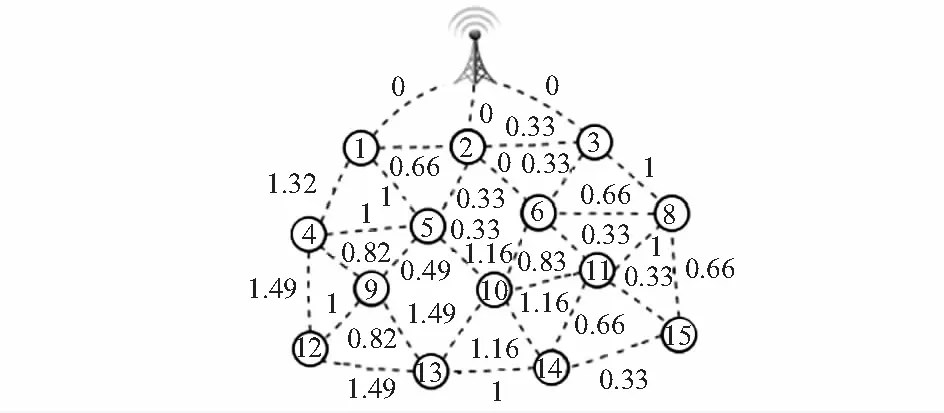
图3 MST-DRN模型的执行流程
2.2 最小Spanning树
在构成了基于边权值的网络拓扑图后,再引用基于Kruskal的多项时间算法,就形成MST。节点总是选择具有最小权值的边传输数据。生成MST的框图如图4所示。以通信图(V,E)、基站和矢量h(能量采集容量)为输入。输出则为以基站为根的MST,即(V,ε,B)。其中ε表示MST中的节点集。

图4 基于Kruskal的MST
仍以图3为例,节点5参与3条边,其中与节点2所构成的边的权值最小,因此,节点5就向节点2传输数据。最终,形成的数据传输有向图,即最小spaning树,如图5。
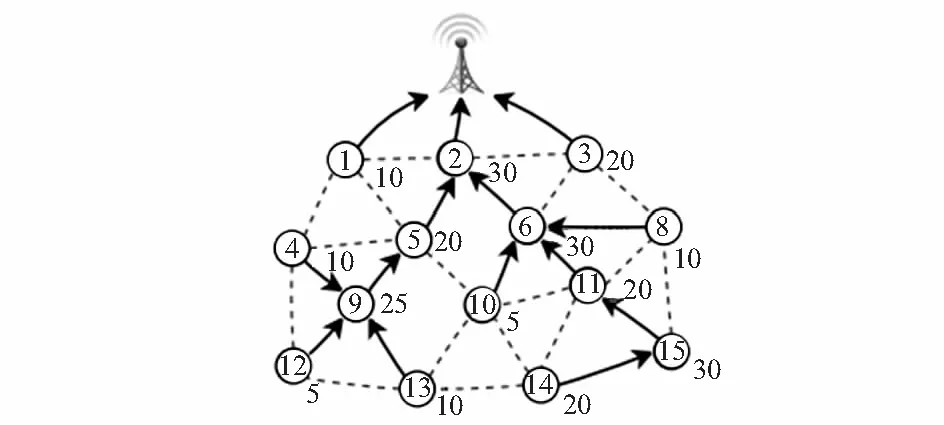
图5 最小spanning树
2.3 基于MST的Ns-LEC搜索法
依据MST,并搜索Ns-LEC节点。搜索过程的伪代码如下。其中R表示Ns-LEC节点集。R初始为空集。
1)输入:(V,E,B,h),MST
输出:R:The set of nodes for which to add the RNs
2)R←∅
3)Calculate the vertices weights
4)∀i∈V,calculatewi
5)(V,ε,B)=MST(E,V,W′)
6)∀i∈V,calculateξiin the resulted tree(V,ε,B)
7)ifξi≠0 then
8)calculateEi=0
9)if the constrained represented is not satisfied forithen
10)R=R∪{i}
11)end if
12)end if
可知,首先计算每个节点的权值wi。再计算每条边的权值Wu,v,并构成边权值矩阵W。再利用Kruskal构成MST树,如步骤(5)所示。
再依据MST树,计算每个节点(假定节点i)的支叶节点数(γi)。如果节点i不是支叶节点,即γi≠0,就利用节点生存条件判断节点是否为Ns-LEC节点;如果是,则将其加入R,即R=R∪i。其中|R|表示需要部署RNs的节点数,|R|越少,成本越低。
依据R部署RNS节点,并由RNS负责转发数据包,从而延缓Ns-LEC节点的能量下降,进而保证网络连通,提高WSNs的应用性能。
3 性能仿真
3.1 仿真参数
引用NS 3[13]网络仿真器建立仿真平台。考虑N个随机在分布于100 m×100 m区域。每次仿真时,从N个节点中随机选择1个节点作为基站,其他节点周期产生数据包传输至基站。数据包大小32 B,节点初始能量为Einit=10 J。
为了更好地分析MST-DRN协议性能,引用最小中继算法(minimum relay algorithm,MRA)[14]、基于整数线性规划(integer linear programming,ILP)推导的成本下限[2]作为参照,并进行性能比较。主要分析部署RNs的节点数,即成本。成本越低,性能越好。
3.2 性能分析
节点数对成本的影响,实验数据如图6所示。
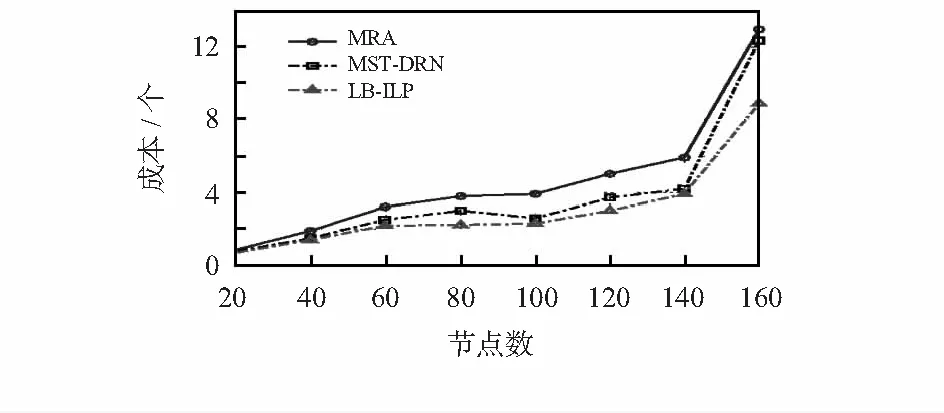
图6 成本随节点数的变化曲线
可知,成本随节点数的增加而呈上升趋势,原因在于:节点数越多,能量低的节点越多。与MRA相比,提出的MST-DRN算法的成本下降,并且随节点数的增加,下降趋势越明显。但与LB-ILP相比,MST-DRN的成本仍具有较大的下降空间。
图7为成本随网络密度的变化情况。其中网络密度是指每个顶点的平均边数。
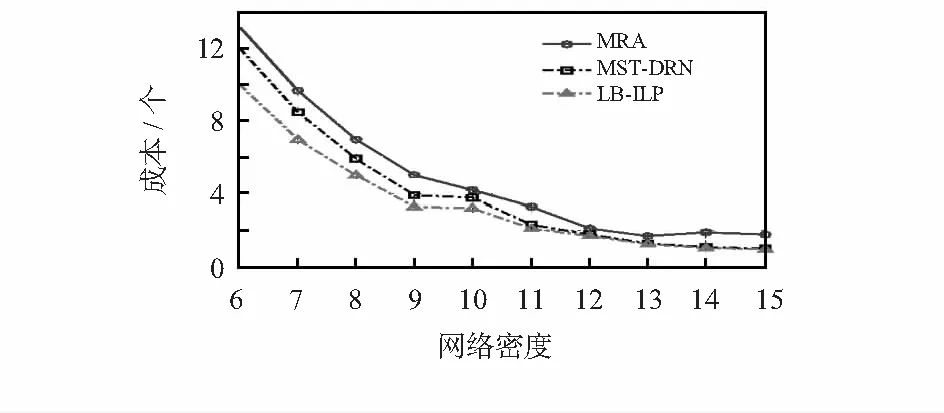
图7 成本随网络密度的变化曲线
可知,成本随网络密度的增加而下降,原因在于:网络密度越大,节点拥有的数据传输支路越多,低能量的节点越少,相应的成本越低。在整个网络密度变化区间,MST-DRN的成本均低于MBA。与图6类似,仍与LBILP的成本存在差异。
数据包传递的性能,如图8所示可知,通过建立最小MST树,构成数据传输的最佳路径,有效地降低了数据包传输时延。此外,通过部署RNs,提高网络连通率,也有利于数据传输效率。
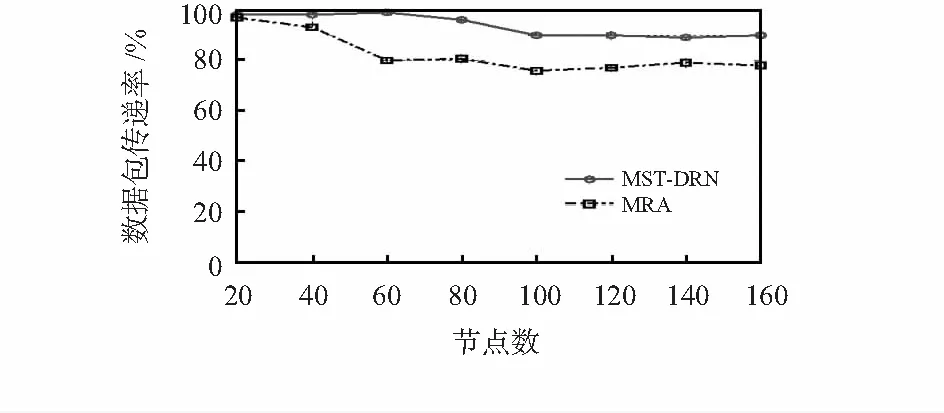
图8 数据包传递率随节点数的变化情况
4 结 论
实验数据表明,提出的MST-DRN算法能以最小成本维持网络连通率,并提高了数据包传输成功率。
