热电偶分数阶传递函数阶次和参数估计

2018-09-26李文军王潇楠郑永军

兵工学报 2018年9期

李文军，王潇楠，郑永军

(中国计量大学计量测试工程学院, 浙江杭州 310018)

0 引言

热电偶被广泛应用于工业测量领域。随着工业测量技术水平的提高，测量瞬态温度的需求也日益迫切和广泛[1-2]。在已有的测量瞬态温度方法中，常用的方法是利用多偶组合实现补偿式瞬态测温，以及利用实验建模技术近似得到系统模型实现瞬态测温。

Enrico等[3]从理论和实验两个角度，对3个温度传感器组合测量瞬态温度和进行动态校准做了对比，讨论了产生精确温度梯度的问题以及保持均匀稳定温度场的问题。吴朋等[4]对于铠装热电偶传感器测量瞬态温度问题，采用支持向量机方法辨识建模，结合量子遗传算法对核函数参数进行优化以减小建模误差，对铠装热电偶传感器测量瞬态温度做精度补偿。Villafae等[5]借助计算流体动力学，用数值实验方法描述了热电偶内部热扩散的演化过程，分析了外部特定测量环境下动态测量误差的产生原因。Doghmane等[6]采用激光器对K型热电偶测量接点产生激励并获得热电偶的响应，分别利用Yag激光器加热获得热电偶在单位脉冲激励下的响应，利用Argon激光器加热获得热电偶在周期性激励下的响应。郝晓剑等[7]针对铠装K型热电偶动态响应误差补偿，采用CO2激光器加热产生激励，并引入红外探测器做辅助测量，获得热电偶的频率特性对热电偶进行补偿。杨庆涛等[8]针对高超声速飞行器地面试验中测量壁面温度的需求，建立了热电偶传感器有限元数值模型，通过传感器内部传热计算，考虑温差项和储能项，分析了热电偶响应特性。上述工作在分析热电偶动态特性时，都采用了1阶或2阶整数阶传热模型，而整数阶导热模型中的时间导数由局部极限定义，表示温度在某时刻的变化，无法表征整个温度的变化历史。

从热电偶与被测介质之间的传热过程看，由于热电偶测量接点存在热惯性，且接点与被测介质之间存在接触热阻和复杂换热[9]，测量接点与热电偶偶丝之间也存在热量传递[10]，故热电偶测量瞬态温度的过程构成了一个物理上的延迟过程或者叫做遗传过程[11]。根据分数阶微积分理论，分数阶微积分具有记忆特点[12]，采用分数阶微积分建立模型能更准确地描述过程的动态特性[13-14]。

本文利用分数阶微积分建立了热电偶偶丝的时间分数阶导热模型，描述了露端式热电偶测量接点与被测介质之间的换热过程。给出了测量固体介质表面的瞬态温度时模型参数的理论值，利用实验系统采集了热电偶输入和输出。最后通过实验数据建模，用改进随机数直接搜索法对传递函数的参数以及阶次进行了估计。

1 热电偶时间分数阶热传导模型

1.1 分数阶微积分定义和分数阶拉普拉斯变换

(1)

式中：f(t)为t的函数；Γ(·)为Γ函数；n为大于μ的最小整数；τ为被积变量。

设算子下限a=0，对于零初始状态，Riemann-Liouville分数阶微积分对应的拉普拉斯变换为

(2)

式中：L表示拉普拉斯变换；s为拉普拉斯算子；F(·)为s的函数。

(3)

(1)式、(2)式和(3)式给出了分数阶微积分算子和对应的拉普拉斯变换。

1.2 热电偶半无限固体传热模型

热电偶由一对有共同接点的材料互异的热电偶偶丝组成，如图1所示。图1中，热电偶偶丝的直径为d，热电偶偶丝1与热电偶偶丝2之间存在一个夹角[16]。

由于热电偶偶丝长度相对于其直径而言很长，且两根热电偶偶丝之间相互绝热，单根热电偶偶丝导热可以视为半无限固体导热问题[17]。热电偶偶丝的半无限固体导热模型如图2所示，图2中：q(t)为热流密度(W/m2)；x为发生热传导方向上的长度(m)；Ts(t)为半无限固体温度分布函数T(t,x)在x=0处的特例。

热电偶偶丝的导热视为半无限固体导热，其热传导方程为

(4)

式中：c为热电偶偶丝材料比热(J/(kg·K))；ρ为热电偶偶丝材料密度(kg/m3)；k为导热系数(W/(m·K))；T0为初始状态温度(K)。

引入过余温度θ(t,x)=T(t,x)-T0，并代入(4)式，得到：

(5)

(6)

当x→-∞， (6)式的边值解为

(7)

(7)式对x微分并取x=0，有

(8)

根据(2)式和(3)式，对(8)式做分数阶拉普拉斯反变换，得到时间分数阶微分形式的关系式为

(9)

根据所定义的过余温度，有

θ(t,0)=T(t,0)-T0=Ts(t)-T0.

(10)

将(10)式代入(9)式并整理得到：

(11)

(11)式等号左侧即热流密度q(t)：

(12)

再定义热扩散系数α(m2·s)：

(13)

并记热电偶测量接点温度与初始状态温度的差Tb(t)=Ts(t)-T0，则(11)式化为

(14)

(14)式给出了半无限固体传热模型下热电偶偶丝热流密度与温度的时间分数阶微分关系式。

1.3 露端式热电偶测量接点的传热方程

当利用露端式热电偶测量介质温度时，传热过程如图3所示，图3中：Tg(t)为被测介质温度与初始状态温度的差；Qi(t)为被测介质到露端式热电偶测量接点的热流量；Q1(t)和Q2(t)分别为热电偶偶丝1、热电偶偶丝2的热流量；A1、k1、α1分别为热电偶偶丝1的截面积、导热系数和热扩散系数；A2、k2、α2分别为热电偶偶丝2的截面积、导热系数和热扩散系数。

根据(14)式，分别有

(15)

(16)

露端式热电偶测量接点的换热方程表示[18]为

(17)

式中：h为热电偶测量接点与被测流体之间的换热系数(被测介质为流体)或者接触系数(被测介质为固体)(W/(m2·K))；A为热电偶测量接点与被测物体之间的接触面积(m2)；m为热电偶测量接点质量(kg)。

(17)式做拉普拉斯变换并整理，得到：

(18)

(18)式给出了热电偶时间分数阶模型下的传递函数，其中s的阶次μ1、μ2分别为1.0和0.5，它是一种固定阶次的分数阶传递函数。由于热电偶在到达稳态温度过程中，并不是一个严格的绝热过程，s的阶次μ1、μ2之间并不一定存在严格比例关系[19]，传递函数可表示为更一般的形式：

(19)

式中：参数a1为瞬态传热过程中测量接点热惯性引起的延迟；a2为瞬态传热过程中温度激励引起的热扩散中单相延迟[20]，也就是热流梯度相比温度梯度的延迟；a3为常数项。

2 传递函数参数的理论区间

2.1 热电偶的热物性参数和几何参数

对于(19)式，在μ1=1.0和μ2=0.5时，参数a1、a2的理论值可表示为

(20)

(21)

在被测介质温度变化幅值较小时，测量接点的导热系数、密度和比热k、ρ、c都可近似视为常数[21]。以一种常用的镍铬- 镍硅热电偶为例，表1给出了热电偶偶丝的热物性参数。

表1 热电偶偶丝的热物性参数

表2 热电偶测量接点的等效热物性参数

表3 热电偶偶丝的几何参数

表4 热电偶测量接点的等效几何参数

2.2 固定阶次分数阶模型参数的理论区间

热电偶测量接点与被测固体表面的接触可以简化为常压下间隙介质为空气的金属表面间接触[24]，其接触系数h理论值介于1 000 W/(m2·K)与5 000 W/(m2·K)之间[25]。根据(20)式，并代入表2中热电偶测量接点热物性等效参数和表4中热电偶测量接点几何等效参数以及接触系数理论值，得到a1的理论值区间。根据(21)式并代入表1中热物性参数和表3中几何参数以及接触系数理论值，得到a2的理论值区间。计算结果见表5.

表5 参数的理论值

虽然理论值存在误差，但是当利用改进随机数直接搜索法等方法估计参数时，上述理论值仍然提供了计算所必须的初始值取值区间。

3 实验系统和实验数据

3.1 实验系统

为了获得热电偶在温度激励下的动态响应，建立了一种实验系统，结构如图4所示，主要包括计算机、美国Measurement Computing公司生产的MCC-USB-2408数据采集卡、日本欧姆龙公司生产的CPM1A可编程控制器、机械往复运动机构以及宁波元创机电公司生产的M12 NPN激光对射开关和日本安立公司生产的ACSⅡ-2000温度标准源恒温面。

实验原理是将热电偶固定在运动机构上，由可编程控制器控制运动机构，驱动热电偶进入定位点，使得热电偶测量接点与恒温面接触并保持，热电偶与恒温面的接触时间用激光对射开关采集，热电偶输出信号由数据采集卡采集和记录。实验中先对热电偶做静态响应标定，再参考温度传感器动态响应校准规程，最后用实验系统获得热电偶在激励下的输出。

3.2 实验数据

实验设定的激励温度区间设定为300～400 K之间，表6给出了实验时的3组实验配置数据。

表6 实验配置

表6的实验配置对应实验数据集散点图如图5所示。数据集时间步长为0.25 s.

对3组数据做归一化处理并平均，取激励发生时间点为起始时间，截取后的数据集长度为101，测量值平均值的散点图如图6所示。

上述测量值的平均值可作为待辨识数据集。为了简便，以下讨论中测量值的平均值仍用测量值指代。

4 热电偶分数阶传递函数辨识

4.1 分数阶传递函数的辨识方法

分数阶传递函数的辨识方法有多种，其中改进Luus-Jaakola算法是Luus-Jaakola算法的优化，它是一种基于随机搜索的优化方法[26]。采用这种方法，首先在参数搜索区间内采用随机搜索的方式获取区间次优值；然后在次优值的基础上自适应改变搜索区间，做下一步随机搜索，最终达到最优结果。这种方法的关键步骤是采用一个可变收缩系数，在每次迭代后，用收缩系数缩小搜索空间以减少搜索时间并达到搜索目标。改进Luus-Jaakola算法的步骤如下：

1)输入要搜索的向量β(模型参数和阶次)；

2)确定评估函数J；

3)产生随机搜索向量初始值β0；

4)迭代计算，直到误差满足要求或者迭代次数达到限定值；

5)选择收缩系数φ，将搜索区间乘以收缩系数；

6)反复迭代到满足评估函数J所确定的性能指标；

在本文算例中，评估函数J采用输出误差平方和形式[27]为

(22)

式中：M为数据集长度；y为预报值；y0为测量值；i为离散时间变量，i=0，1，2，…，M.

4.2 改进Luss-Jaakola算法的验证

为了验证改进Luss-Jaakola算法，首先对于已知的模型结构进行辨识。假设已知模型为

(23)

根据文献[28]提出的Luss-Jaakola算法验证方法，首先由(23)式生成真实值数据集，并增加高斯分布的随机噪声，得到一组模拟测量值数据集；然后根据模拟测量值数据集，用改进Luss-Jaakola算法进行辨识，得到参数和阶次的辨识结果。

上述验证算例中，生成的模拟测量值数据集离散时间步长为0.125 s，数据集长度为201. 定义待搜索参数a1、a2、a3和阶次μ1、μ2构成的向量为

β=[a1a2a3μ1μ2],

向量真实值为

β=[1.20 1.30 1.00 2.10 0.50],

辨识结果如表7所示。表7中真实值为已知模型给出的参数和阶次，估计值为通过模拟测量值辨识得到的参数和阶次。

表7 参数真实值和估计值

输出的模拟测量值、分数阶模型估计值和真实值的比较如图7所示，评估函数J为0.041.

从表7和图7可以看到，Luaas-Jaakola算法的辨识结果较好地逼近了真实值，表明方法有效。

4.3 固定阶次分数阶传递函数参数的辨识

图7所示的测量值数据集，其时间步长为0.25 s，数据集长度为101. 根据(19)式，模型阶次已经确定，是一种呈比例阶次的分数阶结构，其形式为

(24)

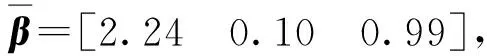
(25)

式中：参数a1为2.24，位于理论值区间[0.48, 2.38]内，表明在固定阶次模型下，引入的测量接点热惯性项与理论估计较为一致，能够刻画热惯性引起的延迟；参数a2为0.10，偏离了理论值区间[0.14, 0.72]，小于理论值区间的最小值0.14，表明在固定阶次模型下，引入的热电偶丝热扩散项与理论估计不一致，虽然表征了热电偶丝热扩散引起的延迟，但是只是延迟的一种弱化表示。输出测量值和固定阶次模型估计值的比较如图8所示。

从图8可以看出，固定阶次分数阶模型在时间轴0～4 s区间时与实验数据不能很好地吻合。从物理过程分析，0～4 s区间内，激励温度与环境温度差较大，热电偶测量接点热物性参数和几何参数本身也在随温度变化而变化，因此参数a1和a2并不是定值，这使得分数阶模型在这个时间区间内与测量值之间仍存在较大误差。

4.4 变阶次分数阶传递函数参数和阶次的辨识

(26)

式中：参数a1和μ1组成项即0.86s2.13项，以及参数a2和μ2组成项即2.28s0.92项，组合表示了测量接点热惯性和热电偶偶丝热扩散所引起的延迟。输出测量值和变阶次模型估计值的比较如图9所示。

从图9可以看出，变阶次分数阶模型在时间轴0～4 s区间与实验数据能较好地吻合。

4.5 固定阶次模型和变阶次模型拟合结果比较

图10是输出测量值、固定阶次模型估计值与变阶次模型估计值的比较，其中固定阶次模型的评估函数J为0.043，变阶次模型的评估函数J为0.020.

从图10可以看到，变阶次分数阶模型克服了固定阶次分数阶模型在时间轴0～4 s区间与实验数据不能很好吻合的缺点，又能反映热电偶整体温度响应的变化特征。由于分数阶算子可视为传统算子微积分阶数在相邻整数值之间的插值，变阶次分数阶模型表达了分数阶微分算子的阶数插值性质。分数阶微积分运算可以被视为幂函数和算子作用函数的卷积，因而更好地描述了热电偶温度分布特征的全局相关性，以及温度分布的记忆和延迟性质。