周期性阵风流作用下通气超空泡的仿真研究

王威, 王聪, 杜严锋, 李聪慧

(哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)

0 引言

自Reichard[1]在1946年首次提出可以采用人工通气的方式生成超空泡以来，对通气超空泡的研究始终是各国学者关注的热点问题。航行体在水中的摩擦阻力约为空气中的850倍，水下航行体借助通气超空泡的包裹，使得航行体表面阻力大幅度减小，航速可以得到突破性提高[2]。

航行体在通气超空泡内部的姿态影响着航行体的沾湿区域，进而改变了它的流体动力。目前相关研究多数是在稳定水流中进行的，通过航行体周期的改变攻角来实现，例如：Lee等[3]设计了可以让模型在水洞试验工作段中摆动的机构，利用试验方法研究了航行体俯仰运动时的通气空泡与航行体尾部的相互作用。Pan等[4]在文献[3]基础上，利用数值模拟方法研究了水洞中的通气超空泡航行体俯仰运动过程中泡内压力变化规律。Yu等[5]研究了航行体以固定频率进行俯仰运动时的流体动力变化特点。当航行体遇到前方不稳定的来流或者航行体靠近海面附近运动时，波浪的作用往往会导致超空泡形态发生变化，在航行体表面形成沾湿区域而增加阻力，严重时甚至导致空泡溃灭。

针对这种问题，Koptiva等[6]通过在水洞中安装由两片水翼组成的阵风发生器，研究了阵风流作用下局部通气空化水翼的升阻比性能。Arndt等[7]通过水洞试验研究了稳定流和阵风流作用下的通气空泡生成和保持机制，给出了所需通气量的大致范围。Lee等[8-9]研究了周期性阵风流扰动下通气超空泡的形态特征，发现阵发生器的频率增大到一定程度时将影响超空泡长度，但对超空泡直径的影响不大；比较了不同支撑方式(前支撑和后支撑)给通气超空泡带来的影响，指出采用前支撑方式容易在超空泡来流方向造成扰动，使空泡表面变得不光滑，后支撑方式对空泡变形有一定的抑制作用，并干扰超空泡尾部的闭合方式。Sanabria等[10]通过试验研究了超空泡航行体的动力学建模及控制，结果表明在阵风发生器作用下，航行体的空化器受到扰动而产生的力和力矩可以忽略，可航行体尾翼受到流动扰动不可忽略。Karn等[11-12]试验研究了通气超空泡尾部的不同闭合模式，并根据试验结果分析了这些模式之间的转变因素，进而分析了水洞阻塞比对闭合模式的影响，指出大阻塞比会导致通气超空泡的尾部以双涡管模式闭合；并研究了阵风流动对空泡尾部闭合模式的影响，发现空泡尾部内外压力的波动变化是导致空化数波动的原因，并影响着空泡尾部以回射流和双涡管这两种模式之间的交替变化。Karn等[13]利用阵风发生器的扰动研究了通气超空泡产生和溃灭中的通气流量，指出形成超空泡所需的通气量与流场速度、空化器尺度、流动不稳定性的因素相关，阵风流动降低了气泡的凝结效率，导致形成超空泡所需的通气量增加。

以上研究多数是采用水洞试验方式对阵风流作用下通气超空泡的形态变化和空泡内外压力进行分析，由于受到试验条件限制，试验研究阵风流作用下的流场垂向速度变化采用单点测量的方式进行，难以捕捉到整个流场的垂直速度变化特点，并且试验中模型的支撑方式对阵风流中超空泡形态的变化也有一定影响。而采用数值模拟方法有利于研究阵风流作用下整个流场的垂直速度变化，并且通气超空泡形态不受支撑结构影响。

本文首先建立周期性阵风流作用下的计算网格模型，利用试验结果对计算方法的有效性进行验证，然后研究阵风发生器产生的阵风流动在整个流场的垂直速度分布，分析周期性阵风流作用下通气超空泡形态变化特点，并利用阵风流作用下的空化数周期波动规律，分析通气超空泡尾部闭合方式的变化原因。

1 数学模型及验证

1.1 数学模型

本文研究中的来流速度较低，自然空化现象较弱，忽略了自然空化影响[14]，采用主动通气形成的超空泡内部基本被空气填满[15]，参照文献[16-17]对通气空泡流动的计算经验，本文采用流体体积函数(VOF)两相流模型对通气超空泡进行数值模拟研究。

1)连续性方程

(1)

式中：ρm=αlρl+αgρg为混合介质的密度，αl为液体体体积分数，αg为气体体积分数，αl+αg=1，ρl为液体密度，ρg为气体密度；ui为混合介质在笛卡尔坐标轴i方向上的速度分量；xi为i轴方向的坐标，i=1，2，3；t为时间。

2)动量方程

(2)

3)体积分数方程

(3)

如果网格单元充满水，则αg=0；如果网格单元充满气体，则αg=1；如果网格单元中包含气体和水的分界面，则0<αg<1.

4)湍流方程。根据文献[18-19]对通气空化流动的计算方法，本文选择RNGk-ε湍流模型进行数值模拟研究。该模型由Yakhot和Orzag提出，可以很好地处理高应变率和流线弯曲程度较大的流动，湍动能k和湍动能耗散率ε的输运方程如下：

(4)

(5)

1.2 数值求解方法及边界条件

1.3 模型验证

本文数值模拟所得监测点K的垂直速度变化结果和水洞试验[8]结果对比如图3所示。从图3可以看出，在f=20 Hz和θ0=±6°的周期性阵风流动条件下，监测点K的垂直速度产生了三角函数变化，数值模拟和水洞试验监测点垂直速度变化结果有很好的一致性。进一步分析数值模拟阵风流作用下的通气超空泡形态变化和水洞试验[8]结果对比如表1所示。由表1可见，数值模拟得到的通气超空泡形态和试验中空泡形态的变化规律一致，充分表明本文数值模拟方法的有效性。

2 模拟结果分析与讨论

2.1 波长及波幅

使用阵风发生器可以模拟不同的海况条件，通过垂直速度监测点得到的最大垂直速度和阵风发生器频率可以计算不同海况条件下的波长和周期[8]。但是试验中的这个单点监测不足以显示整个流场垂直速度的变化，并且监测方法受水洞试验条件的影响较大，因此利用数值模拟方法研究上游的阵风发生器摆动对下游流域垂直速度的影响就成为本文关心的问题。

在阵风发生器下游，从空化器的所在位置到流域尾部布置一条监测直线，在阵风发生器最大摆动角度不变条件下，经过几个周期后水翼摆动到平衡位置时，比较不同频率f和来流速度v∞对流域垂直速度的影响，具体计算结果如图4和图5所示。

从图4可以看出，来流速度v∞相同时，阵风发生器频率f越大，下游流场中形成的波长越短、波幅越大；从图5可以看出，阵风发生器频率相同时，来流速度v∞越大，在下游流场中形成的波长越长、波幅越大。由于流域波长λ等于来流速度除以阵风发生器频率，即λ=v∞/f，波幅随着阵风发生器摆动角度的增大而增大。从图4和图5发现波幅向下游不断衰减，来流速度越小、衰减越快。因为来流速度较大时可以迅速地将阵风发生器产生的扰动能量传递到下游流域，从而产生较大的波幅，而来流速度较小情况下，阵风发生器的扰动能量还没有及时传递到下游就已在流动介质内部因摩擦阻力的影响而损失。

提取v∞=8.34 m/s时流域中距离中心线不同距离的径向位置上垂直速度分布，如图6所示，从中可以看出垂直速度的幅值随着远离流域中心而衰减。综合图5和图6的速度分布可知，在进行超空泡流动问题研究时，要尽量将模型和空泡的位置安排在流域中垂直速度衰减不大的区域。

2.2 空泡形态演化过程

在阵风流作用下，水洞模型的支撑方式对通气超空泡存在影响，研究结果表明支撑方式对通气超空泡最大直径的影响较小，但对空泡长度的影响较大，空泡长度随着阵风发生器频率的升高而变短[8-9]。采用支撑结构在模型下游的后支撑方式，下游支撑结构对通气超空泡的尾部闭合存在一定影响，而采用支撑结构在模型上游的前支撑方式，虽然空泡形态不受模型后部的支撑结构影响，但是模型前部的支撑结构仍然会在上游造成一定扰动，使空泡形态变得不够清晰。利用单独空化模型数值模拟研究周期性阵风流作用下的通气空泡多相流问题，可避免支撑结构的不利影响。流域的具体布置如图7所示。

由于空泡长度受长波的影响较小，受短波的影响较大，水洞试验[8]中波长的改变是通过改变阵风发生器频率f实现的，但是试验并没有研究来流速度对波长及波幅的影响，研究不同来流速度造成的阵风流波长对下游通气超空泡形态的影响还没有相关文献涉及，在阵风发生器频率f=20 Hz、最大摆动角度θ0=6°条件下，数值计算所得单独空化器在不同波长条件下的超空泡形态如表2所示。

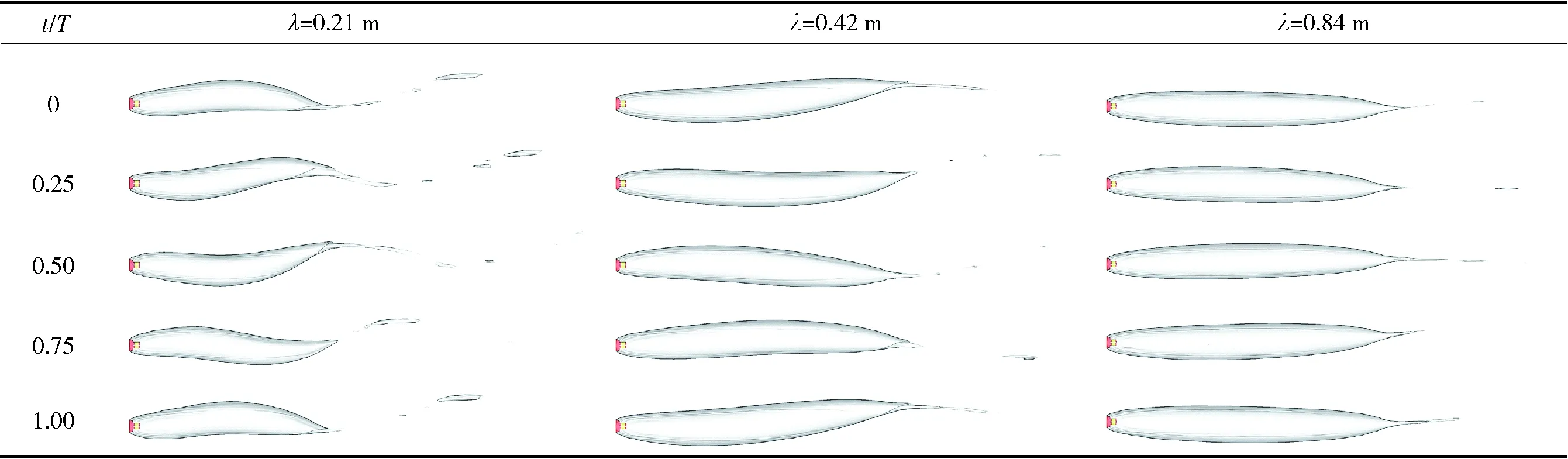
表2 不同波长条件下一个周期中各个时刻的超空泡形态

从表2可以看出：随着波长λ增加，阵风流动对超空泡形态的波动影响减弱，λ=0.21 m时，超空泡长度占整个波长的71%，空泡形态受到来自垂直速度方向的扰动范围大，空泡表面上下相对运动的趋势较大，空泡波动明显；λ=0.42 m时，超空泡长度占整个波长的52%，空泡形态受到垂直速度方向的扰动范围减少，空泡表面上下相对运动的趋势减少，空泡波动现象减弱；λ=0.84 m时，超空泡长度占整个波长的27%，空泡形态受到垂直速度方向的扰动进一步减少，空泡表面上下相对运动的趋势大幅减少，空泡波动现象不明显。即在阵风流作用下，空泡长度占有波长的比例越小，整个空泡表面的整体运动趋势越趋于一致，空泡形态的波动越弱。由此可知，通气超空泡形态在来流速度较高的环境中更稳定。

2.3 空化数对超空泡尾部闭合方式的影响

由图8可见，通气空化数在阵风流作用下出现了周期性波动现象，且一个周期内该空化数的最大波峰值和最小波谷值并不相同，这是因为重力作用致使阵风发生器的水翼向上和向下摆动，对流域造成的压力扰动效果不同。超空泡尾部的双涡管泄气现象在空化数增大时变得微弱，而在空化数减小时变得明显，这种空泡尾部的涡管泄气现象随着空化数的波动变化。空泡尾部闭合方式如图9所示，图9中：A为流域截面面积；An为空化器截面面积；Ac为空泡尾部控制体V左侧的空泡截面面积；ui为通过Ac面进入控制体V的空气速度；pRJ为双涡管间的回射流动量；Ao为双涡管的截面面积；uo为通过Ao的气体速度；ARJ是进入控制体V右侧液体回射流截面面积；uRJ是回射流速度；po是空泡尾部的压力。

根据流体力学的动量方程

(6)

(7)

即在单位时间内净流出控制体V的动量之和等于外界作用在控制体上的合外力，流出的动量取+号，流入的动量取-号。

结合图9所示的通气超空泡闭合示意图，根据Nesteruk[20]的方法，假设通气超空泡内部的压力pc相同，根据(7)式对空泡尾部闭合区域的控制体V给出动量方程如下：

(8)

由于此时刻的空泡形态相对稳定，进入空泡尾部控制体的气体动量与液体动量相比可以忽略[11]，(8)式可简化为

(9)

同理，对图9的整个控制体给出动量方程如下：

(10)

整理得

(11)

式中：FD为空化器阻力；CD为空化器阻力系数。

将(11)式代入(9)式，整理得

(12)

(13)

在来流速度v∞和通气率Cq恒定情况下，若远场压力p∞和空泡内部压力pc相对稳定，则通气空化数相对稳定。但由于阵风发生器的摆动，引起了压力p∞和pc的波动变化，进而导致通气空化数的波动。由于阵风流对超空泡直径影响较小[8]，可认为此刻(13)式中空泡截面Ac的变化不大，空化数σ变化导致了回射流动量pRJ的波动，pRJ随着空化数σ的增加而增加，回射流波动使得空泡尾部的双涡管泄气方式形成周期性改变。

3 结论

本文建立了周期性阵风流作用下的流场数值计算模型，得到了阵风流作用下的通气超空泡形态，并通过与文献[8]试验数据对比，验证了所建立模型的正确性。基于所建立的模型，数值模拟研究了阵风流作用下流场垂直速度分布及通气超空泡的变化特点。所得主要结论如下：

1)阵风发生器频率越小、来流速度越大时，流场波长越大，波长λ大小等于来流速度v∞和阵风发生器频率f的比值；阵风发生器的摆动角度越大、频率越高，在下游产生垂直速度波动的幅度越大，并且这个波动幅度沿下游减少，来流速度越小，减小得越快。

2)流场下游的通气超空泡受到阵风发生器的影响产生波动，超空泡长度占有波长的比例越小，空泡波动变形越小，阵风发生器作用下，来流速度越高，通气超空泡的形态越稳定。

3)空化数受到阵风流的影响而出现周期性变化，超空泡尾部的涡管泄气方式也出现交替性变化。空化数变大时，超空泡尾部回射流的动量增大，双涡管泄气方式消失；空化数变小时，超空泡尾部回射流的动量减小，双涡管泄气方式出现。