在习题教学中渗透物理思想方法
2018-09-22周鹏
周 鹏
(江苏省扬州中学 225009)
当今社会十分强调教育对于人的科学素养的培养,国内教育界普遍认为,科学素养架构应该包括如下三个基本维度: 科学知识与技能; 科学探究过程、方法与能力; 科学态度、情感与价值观.细化到具体学科的层面,物理学科核心素养主要包括以下四个方面:形成物理基本观念;掌握科学探究方法;形成良好科学思维;培养正确科学态度.不管从哪个层面上讲,科学的思想方法对于生活、学习或研究都属于核心层次的基本素养,是今后独立学习和研究的基础.所以,在平时的物理教学中,我们应当特别重视对学生进行物理思想方法的适时渗透,培养学生自主的思维意识和良好的思维习惯.常见的物理思想方法主要有:图形/图像图解法、极限思维法、平均思想法、等效转化法、猜想与假设法、整体与隔离法、临界问题分析法、对称法、寻找等/恒量法、理想模型法、估算法、微元法、解析法、类比法、比例法、逆向思维法等等.
现以一道常见的几何光学题来说明在习题教学中如何有效地进行物理思想方法的渗透.
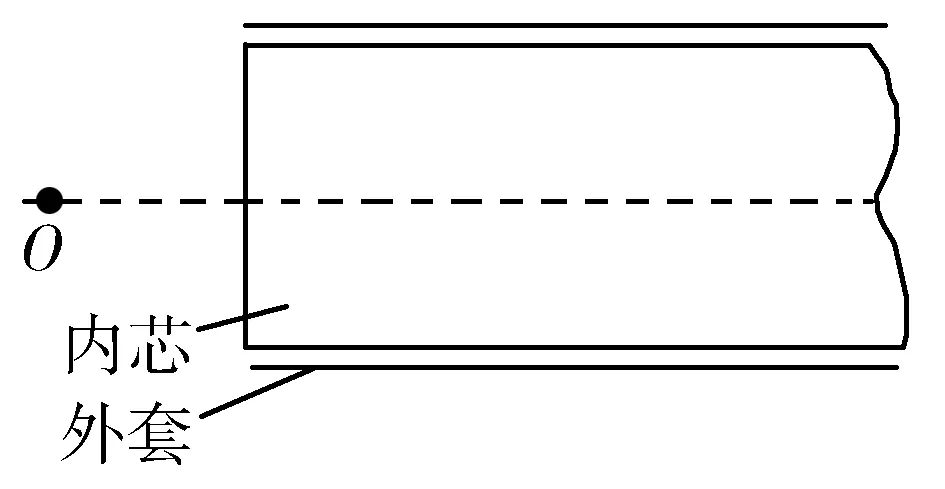
图1
例题光纤通信的主要优点是容量大、衰减小、抗干扰性强,载有声音、图象以及各种数字信号的激光从光纤的一端输入,就可沿着光纤传到千里之外的另一端,实现光纤通信.某光纤内芯半径为a,内芯的折射率为n,传递的信号是从光纤的轴线上O点射向光纤,如图1.
(1)若该长直光纤长为L,求光在该光纤中传播的最短时间;
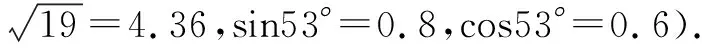
解析(1)由于光在介质中的传播速度由介质和光的频率决定,故本题中的光速为定值,从而当光的传播的路径最短时,传播的时间就最短.通过简单的光路分析可知,当光垂直于左端面射入时,传播的路径最短.
平直空间里两点间直线距离最短,所以在题目中的第一问中,必须加上“长直光纤”这一条件,否则仅由题中条件无法求得最短时间.而这一条件在很多的参考资料中都被忽视了,不过这样就为做题和讲解时的“图解法”思维引导训练提供了机会.该问题可以在教师的提醒下由学生自行分析完成,提醒的目的则是在引导学生用图形分析法使自己的思维更严谨.
光在介质中传播的速度v=c/n,传播的最短路径为L短=L,则最短时间t短=L短/v=nL/c.
(2)就单纯解题而言,因为题目中要求要发生全反射,所以我们可以通过光信号在光纤内芯中传输时相对外套的临界角,得出光在左端面上射入光纤时的折射角,再根据折射定律得出相应的入射角,最终再利用几何关系求出O点到光纤端面距离的最小值.过程如下:

同时,为保护辖区人民群众“舌尖上的安全”,他带领全体干部落实好“治理餐桌污染、建设食品放心工程”“食品放心工程三年行动”方案和“全国文明城市”创建等工作任务,深入排查整治食品药品安全隐患,严厉查处食品药品违法违规行为,守住了涵江不发生食品药品安全事故的底线。2014年组建以来,分局共开展食品药品安全执法检查100多次,抽检各类食品药品1500多批次,查处各类食品药品案件290余件,罚没金额360余万元,办案成效得到福建省食品药品监管局的通报表扬。
但如果就这样讲一下,题目的作用根本不能有效地发挥出来.这里还有一个思维引导很关键,就是为什么会存在一个最短距离.这需要学生充分利用图形分析的直观优势,通过改变O点的位置,来发现距离x对光线的影响,从而才能真正体会到上面解题过程中为什么要从临界角开始算起.
为了使该题目的效能最大化,我们还需要作进一步的拓展.
拓展1 若光纤的外套材料用空气替代,那么内芯的折射率n满足什么条件时,光源O可以放在任意位置,都不会造成光线从侧面泄漏?
解析对于该问题的处理,可以看出学生对光源O离左端面的最短距离是否真正理解了,同时可以引导学生充分运用临界和极限分析法来处理光学问题.
利用图解法和极限分析法,结合上面的分析可知,若光源O紧贴着光纤的左端面,可以认为光从空气中以90°的入射角掠射到左端上,则折射角最大,为临界角C,再入射到侧面上时的入射角达到最小,为i2小= 90°-C.
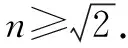
拓展2 若光纤的外套材料用空气替代,内芯的折射率n,则光信号在不会发生侧漏的前提下,从其左端面传到右端面所需的最长时间为多少?
解析根据前面的分析,学生很容易通过图形法分析得到:光在光纤中反射的次数越多,其通过的路径越长,所需的时间也就越长.而且,要使光信号在不会发生侧漏,则在侧面上的入射、反射角最小应等于临界角C.但接下来的处理思路则会有多种情况,涉及到的物理方法也就会有所不同.典型方法如下.

图2
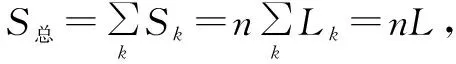
方法二等效法.依照图2所示,根据对称性及几何关系可知,光在光纤中的实际传播光路ABCDEFG的长度,可以等效处理成线段AH的长度,且∠AHG=C,则光在光纤中的总路程S总=AH=L/sinC=nL,亦可得t总=S总/v=n2L/c.
方法三速度分解法.由于光在光纤中来回反射时速度大小不变,时间最长时任意一段光线跟侧面间的夹角恒为临界角C,可以发现,光在任意一段传播时,其速度沿光纤轴线方向的分量v∥≡vsinC=c/n2,所以t总=L/v∥=n2L/c.
拓展3 以上各种解法都是建立在光在侧面上恰好发生全反射的基础上的.而通过[拓展1]的讨论可知,光纤内芯的折射率越大,左端面处的折射角越小(在时间最长的要求下,该处的折射角应等于C),在侧面处的入射角θ=90°-C就越大.可见,折射率较大时,光在侧面处的入射角θ就有可能始终大于临界角C,则上述三种解法中的“sinC”因子就都应换成“sinθ”.
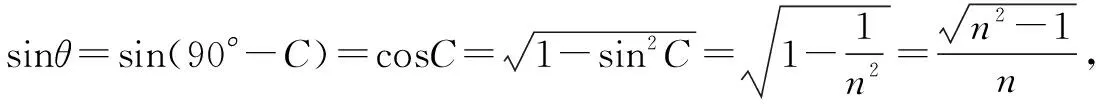
科学素养的的核心就在于能够自主地、有目的地进行科学探究,并能够在探究过程中充分展开科学思维,灵活运用各种科学的方法.当知识用来解决问题时,知识将发挥它的思维训练价值.从物理学科角度讲,我们不仅要处理好物理概念和规律的教学过程,还应当充分重视在习题教学中充分发挥知识的价值,适时地进行物理思想和方法的渗透,这是培养学生科学思维,强化学生核心素养的最有效途径之一.
