基于原始振动信号的往复压缩机卷积神经网络故障诊断
2018-09-22杨洪柏张江安张宏利刘树林
杨洪柏,聂 昂 ,张江安,张宏利,刘树林
(1.上海开放大学理工学院,上海 200433) (2.上海大学机械工程与自动化学院,上海 200072) (3.上海工程技术大学高职学院,上海 200437)
智能故障诊断一般包括特征提取和模式识别两个步骤。常用的特征提取技术包括时域统计分析、小波变换、经验模态分解(EMD)和傅立叶频谱分析等。常用的模式识别分类器包括k-最近邻分类器(KNN)、人工神经网络(ANN)或称多层感知器(MLP)、支持向量机(SVM)。对于往复压缩机的智能故障诊断,不少学者在上述技术基础上做了许多探索研究[1-4]。但由于往复压缩机结构复杂,冲击激励源较多,振动信号表现出复杂的随机特性和非线性,有效的特征提取相对困难,故障诊断效果还不够理想,在线故障诊断也很难实施。
深度网络和深度学习的概念被正式提出后,迅速成为研究的热点,依靠强大的学习性能,其在语音识别、图像识别和人工智能等方面取得重要进展[5]。一些研究者尝试使用卷积神经网络(convolutional neural network, CNN)来诊断机械零件的故障[6-12]。CNN最早应用于图像识别并取得较大的成功,它非常适合于输入是2D(二维)数据的计算机视觉应用。在故障诊断问题中,CNN的输入有2D信号(例如频谱图像),也有1D(一维)信号(例如时间序列信号或频谱系数)。Abdeljaber等[6]提出的模型使用1D振动信号作为输入,它可以执行实时损坏检测。Guo等[7]提出一个分层自适应深度CNN模型,该模型具有两个分层排列的组件:故障确定层和故障大小评估层。Janssens等[8]提出了用于旋转机械状态识别的CNN模型,其输入是所采集信号的快速傅立叶变换(FFT)图谱。Zhang等[9]提出了一个采用原始数据作为输入的CNN模型,用于轴承故障诊断。文献[10]使用短时傅立叶变换将信号转换为时频图,然后用CNN模型进行故障诊断。文献[11]提出了具有两个softmax分类器的CNN网络结构,用一个网络解决两个非独立分类问题。Ince等[12]提出了用于电机故障检测的CNN模型,其输入为1D原始时间序列数据。
上述研究在各自应用领域中都取得了不错的成绩,然而目前还未有用于往复压缩机故障诊断的CNN模型。从上述研究可以看出,应用原始信号输入有其独特的优势:1)直接应用原始振动信号可以避开耗时的特征提取过程;2)对于复杂系统的信号处理,选择合适的特征函数需要大量的机械专业知识和丰富的数学知识,相对很难提取出有效的特征。CNN深度学习模型能够直接从原始信号中提取特征并进行数据分类,而不需要特征提取或手动选择。往复压缩机由于其结构复杂,冲击激励源较多,难以提取有效的特征,故障诊断效果还不够理想,本文拟构造基于原始振动信号的CNN模型(convolutional neural network with raw vibration signal,RVCNN)对往复压缩机进行故障诊断。
1 CNN结构与原理
CNN是典型的深度学习模型框架之一。它是一个典型的前馈神经网络, 其实质是构建多个能够提取输入数据特征的滤波器,通过这些滤波器对输入数据进行逐层卷积及池化,逐级提取隐藏在数据之中的拓扑结构特征,随着网络结构层层深入,提取的特征也逐渐变得抽象,最终获得输入数据的平移、旋转及缩放不变的特征表示。
CNN的典型拓扑结构如图1所示。网络输入为2D的特征图,通过卷积核(神经元的权值矩阵)卷积运算映射到隐层,隐层主要由多组的卷积层(C层)与池化层(P层)组成,C层与P层交替重复,本层的输出作为下一层的输入,如此往复循环[11]。
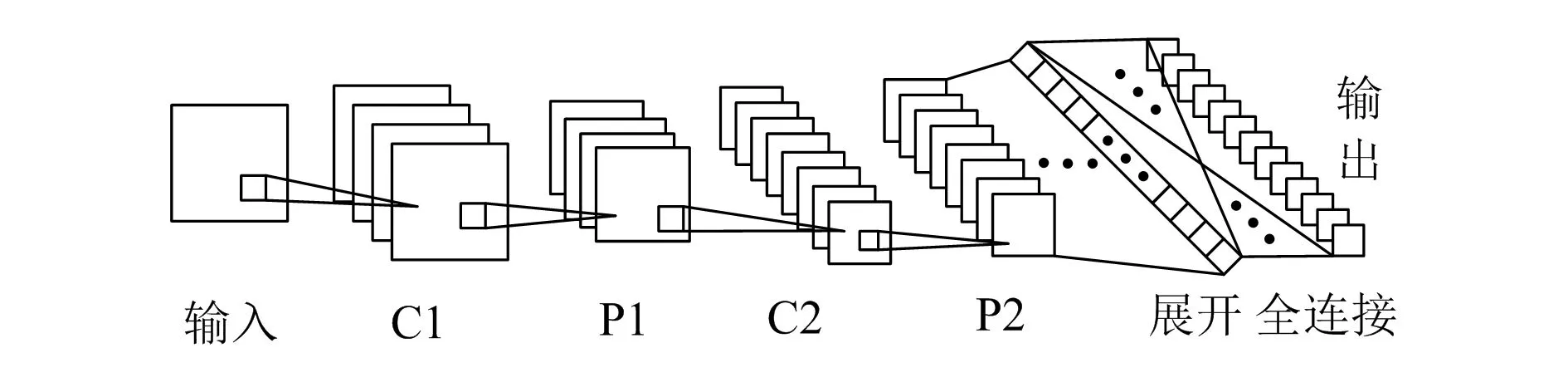
图1 CNN的典型拓扑结构
CNN的卷积层用来提取输入神经元数据的局部特征。每个卷积层均由多个特征矩阵组成,每个特征矩阵为一个平面,同一平面上对应的卷积核相同,具有旋转、位移不变和权值共享的特性,可以并行学习特征,极大减少了自由参数的数目[5,12]。不同平面所对应的卷积核不同,多卷积核使得特征提取更为充分。卷积操作的数学模型可表达为:
(1)
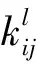
池化层(P层)也被称为下采样层,其作用是对上一层数据图进行缩放映射,以达到减少数据维度的目的。P层提取的特征具有缩放不变性,同时还可以防止过拟合。P层神经元的计算方法如下:
(2)
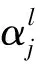
CNN 的输出层采用上一层级特征图进行线性全连接,一般采用softmax分类器,可以解决多分类问题。
目前CNN多为一种有监督的深度模型架构,网络的训练类似于传统的人工神经网络训练方法,采用反向传播算法(BP)将误差逐层反向传递,使用梯度下降法调整各层之间的参数。
CNN的主要特征是结合稀疏连接、权重共享、空间或时间上的降采样共同实现数据的分类处理。稀疏连接通过拓扑结构建立层与层之间非全连接空间关系来降低训练参数的数目;权值共享能够有效地避免算法过拟合;下采样充分利用数据本身包含的局部性等特征,减少数据维度,优化网络结构,且能保证在一定程度上的位移不变性。CNN非常适合海量数据的处理和学习,通过逐层抽取特征,可有效实现故障诊断与识别[5,11]。
2 基于原始振动信号的RVCNN模型
针对往复压缩机故障诊断,提出如图2所示的RVCNN模型,该模型利用1D原始振动信号作为输入,不需要先提取特征,利用CNN自身所具有的学习能力对往复压缩机振动信号进行特征提取和故障诊断。

图2 基于1D原始振动信号的RVCNN模型
经过多次试验调整,基于原始振动往复压缩机的CNN故障诊断模型采用如表1所示的网络模型结构。Dropout概念是Hintion于2012年提出的[9],在每个训练批次中,通过忽略一定比例的特征检测器(让相应隐层节点值为0),从而大大减少过拟合现象,这种方式可以减少特征检测器间的相互作用。第一个全连接层采用ReLU激活函数,它能克服梯度消失问题,大大加快训练速度。第二个全连接层采用softmax分类器进行分类。

表1 RVCNN网络模型结构
3 试验验证
为了探讨RVCNN模型对往复压缩机故障诊断的效果,设计了两个实验:一是应用构造的RVCNN模型对1D原始振动信号进行特征提取和故障诊断,并与常用的功率谱能量(BP)模型和小波包能量(BP)模型进行对比;二是研究RVCNN模型对噪声的鲁棒性,采用不加噪的原始数据对RVCNN模型进行训练,用不同信噪比的数据进行诊断测试,并与小波包能量(BP)模型进行对比。
3.1 试验数据采集
往复压缩机振动实验数据从大庆天然气公司南区压气站1号工作机组上采集而来。为得到不同状态下的往复压缩机振动试验数据样本,在南区压气站1号工作机组的二级气缸上依次安装了正常、阀片断裂、弹簧损坏及阀片有缺口4种状态的气阀进行故障模拟试验,二级气体出口压力1 040kPa,进口压力310kPa,出口温度104℃,进口温度32℃,气体流量3 611m3/h,加速度传感器布置在气阀的阀盖上,采集系统选用INV306U-6660 智能数据采集处理分析仪与北京东方振动和噪声技术研究所的 INV-1021程控多功能信号调理器,采样频率为 20kHz,正常状态采集了120 000个点,其他3种气阀状态各采集了80 000个点。
3.2 训练样本与测试样本库生成
为了获得大量的训练和测试样本,数据采集采用部分重叠切取方式,如图3所示。从仿真实验可知,训练数据的多少也会影响训练的正确率,训练样本越多,准确率越高,本文选取每隔10个数据采集1个样本,每个样本长1 024个数据点,共采集5 382个样本,随机抽取其中的70%作为训练样本,30%作为测试样本。
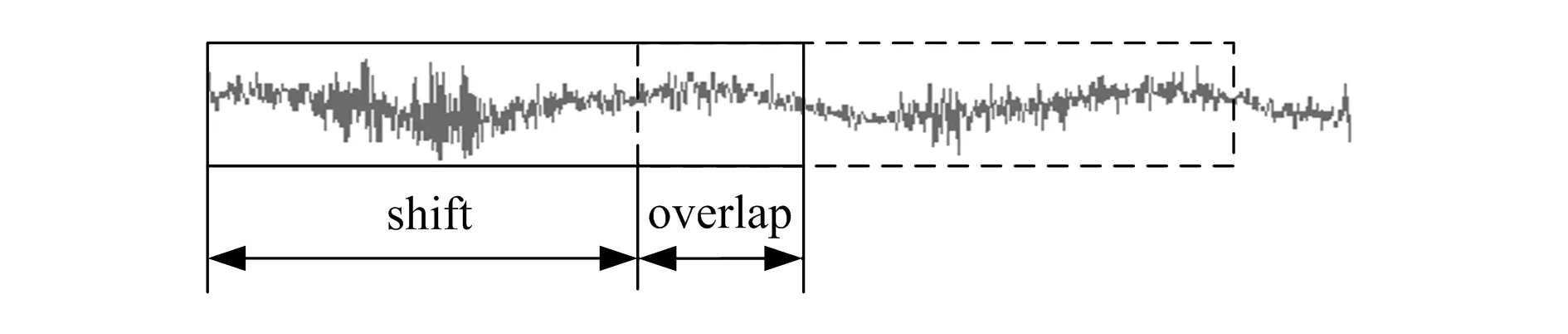
图3 RVCNN样本采集方式
对于功率谱能量(BP)和小波包能量(BP)模型,分别取阀片正常、阀片断裂、弹簧损坏及阀片有缺口4种状态的工作样本各78个,每个样本长度为1 024个数据点。任意选取原始数据下每种状态的40个样本构成故障训练样本(共160个),其余的样本构成模型的测试样本(共152个)。
为了测试不同噪声情况下的模型识别率,在测试样本添加不同信噪比高斯噪声,然后进行测试以获得相应的识别率。
3.3 试验结果对比分析
在未添加噪声的情况下,分别用功率谱能量(BP)模型、小波包能量(BP)模型与RVCNN模型对往复压缩机气阀故障进行诊断对比,功率谱能量(BP)模型识别率只能达到60%,小波包能量(BP)模型识别率达到93.75%,而RVCNN模型识别率可达100%,可以有效地对往复压缩机气阀故障进行识别诊断。
表2是RVCNN模型和三层小波包能量(BP)模型在不同信噪比测试样本下的识别率对比结果,由表可知, RVCNN模型对加不同信噪比噪声的故障信号具有相当高的识别率,无噪声、信噪比分别为50dB和20dB的情况下仍能得到100%的故障识别率,只有在信噪比为10dB的情况下有所下降,但也有90.20%的识别率。而相对的,小波包能量(BP)模型在无噪声情况下的测试识别率也能达到 93.75%,在噪声含量较少的情况下(信噪比为50dB)识别率下降较少,能达到 87.50%,但是信噪比达到 20dB 后,识别率大为降低,无法进行有效识别。
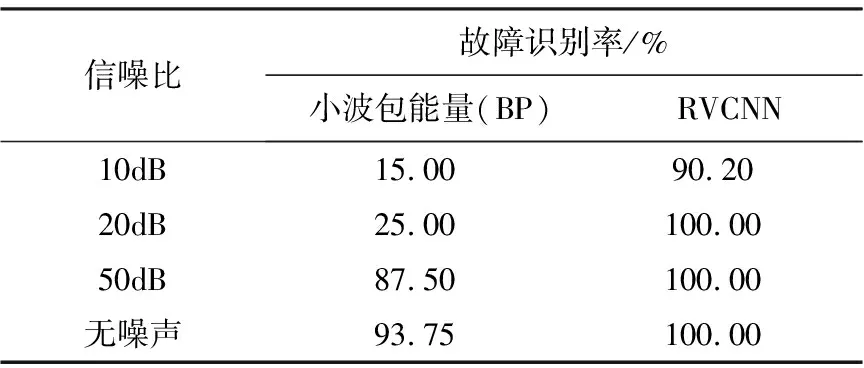
表2 不同噪声强度下故障识别率对比
4 结束语
本文直接应用未加工的1D振动信号作为输入,构造RVCNN模型进行往复压缩机故障诊断。使用从试验台获得的压缩机气阀故障数据样本进行实验,并与小波包能量(BP)模型方法进行比较。用不同信噪比的加噪故障信号进行测试,结果表明,在不同信噪比情况下RVCNN模型识别率均具有较大的优势。这说明RVCNN模型不仅具有较高的识别效果,而且具有一定的抗噪性能。
目前本文只是用1D数据进行尝试,构造模型的层数及各个参数都是基于实验进行调整,未来期望通过进一步研究找出其中的固有规律以供模型优化。
