跨坐式单轨弹性车体和转向架耦合振动分析

成金娜，周劲松，王超冉

(同济大学铁道与城市轨道交通研究院，上海 201804)

跨坐式单轨具有造价低、弯道半径小及车辆运行噪声低等特点，已广泛应用于国内外许多城市。对跨坐式单轨车辆车体进行轻量化设计，在降低车体承载结构质量的同时，导致车体刚度大幅下降。车体刚度过低会导致车体垂向弯曲，可能会引起车体与转向架产生共振。随着车体轻量化，在进行车辆稳定性和舒适性分析时必须考虑部件的弹性，这也成为国内外学者近年来研究的热点。宫岛等[1]对高速列车弹性车体和转向架耦合振动进行了分析；李丽和王瑞卿等[2-3]建立了刚柔耦合动力学模型，对地铁车辆的耦合振动进行了分析。也有一些学者研究了如何抑制车体弹性振动，宫岛[4]、周劲松等[5～6]通过加装吸振器、采用最优控制以及被动控制的方法，较好地抑制了车体一阶弯曲模态的结构振动；黄彩虹等[7]研究了牵引拉杆纵向刚度对高速客车车体弹性振动的影响。以上研究针对的均是铁道车辆弹性车体，尚未有学者对跨坐式单轨弹性车体和转向架的耦合振动进行研究。跨坐式单轨采用胶轮走行，为改善弯道通过性能，部分车型采用单轴转向架，其转向架点头和浮沉运动较为明显。基于上述调研，本文建立了车体弹性振动的刚柔耦合系统动力学模型，研究了车体低阶振动与转向架耦合振动对车辆运行平稳性的影响，分析了弹性车体与转向架的垂向耦合振动，探究跨坐式单轨车辆弹性共振的原因。

1 车辆运行平稳性指标

本文采用Sperling指标评价跨坐式单轨车辆的运行平稳性。根据GB/T 5599—1985标准，运行平稳性Sperling指标的计算式为：

(1)

式中：W为平稳性指标；A为振动加速度，g；f为振动频率，Hz；F(f)为频率修正系数。

根据平稳性指标确定车辆运行平稳性的等级，具体见表1，垂向和横向采用相同的评定等级。

表1 客车Sperling运行平稳性指标

2 车辆系统模型

为了建立车体刚柔耦合动力学模型，运用HyperWorks建立车体有限元模型，计算生成包含车体结构及模态信息的fem文件，并将该文件通过相关接口导入动力学软件Simpack中，完成弹性车体-刚性转向架的刚柔耦合多体动力学模型的建立。

2.1 弹性车体缩聚

针对某跨坐式单轨拖车车体，运用有限元软件Hypermesh划分其模型网格，进行模态计算(如图1)，然后将计算结果导入动力学软件Simpack中。为了减少刚柔耦合系统运算量，同时尽可能保留原弹性车体信息，需要对弹性车体进行缩聚。Guyan[8]提出了在静态结构分析中可以对研究对象的刚度矩阵进行缩减的理论，通过矩阵运算保留系统的主要自由度，消除[9]影响小的从自由度，从而减少计算量。缩聚是将弹性车体看作有限元模型节点的集合，列出节点坐标方程、动能矩阵T、势能矩阵W及能量耗散矩阵Γ，应用拉格朗日方法得到该节点的动力学方程，通过矩阵组装法得到整个弹性体的动力学方程：

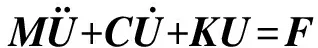
(2)

式中：U为节点状态向量；F为载荷矩阵;M为质量矩阵；C为阻尼矩阵；K为刚度矩阵。

图1 跨坐式单轨车体模态图

车体缩聚后的模型如图2所示，图中的圆点是缩聚选用的重要节点。Guyan缩聚法可保留原模型车体的大部分信息，尤其是弹性变形信息。为了校核模型的准确性，对缩聚前后的模型进行模态对比分析，见表2。与车体平稳性关系最大的典型模态是垂向一阶弯曲，由缩聚前后车体主要典型模态值可以看出，缩聚计算前后，典型振型的模态频率相差较小，垂向一阶弯曲模态频率基本一致(误差仅为0.43%)，表明缩聚后的模型是准确的。

图2 车体缩聚后的模型

典型振型缩聚前频率/Hz缩聚后频率/Hz误差/%1阶菱形7.397.311.081阶扭转12.2412.461.801阶呼吸14.7314.283.011阶横弯15.0014.920.531阶垂弯12.4112.460.43

2.2 车辆动力学建模

跨坐式单轨单节车辆的刚柔耦合动力学模型如图3所示，包括1个车体、2个构架、8个走行轮、8个导向轮和4个稳定轮刚体。与车体相比构架弹性变形相对较小，因此考虑将其视为刚性；空气弹簧的垂向、横向和纵向刚度简化为线性弹簧，走行轮和水平轮视为各向同性的线性弹簧，抗点头装置等效为转向架和车体之间的扭转弹簧，布置在转向架两侧。在模型中考虑以下非线性因素：弹性止档刚度、垂向液压减振器阻尼系数等。根据GB/T 5599—1985标准，在Simpack后处理中设置车体振动测点Sensor1和Sensor2，分别布置在转向架中心左右1m处(对应车体坐标系坐标分别为(6,1,0.5)、(-6,-1,0.5))。

图3 单轨车辆动力学模型

3 弹性车体对运行平稳性的影响

轨道激励采用ISO8608标准A级公路谱，系数取为0.5。基于刚柔耦合动力学模型，通过仿真分析车辆在不同运行速度下弹性车体和刚性车体的垂向振动加速度(图4)和运行平稳性，根据式(1)求出车体垂向和横向运行平稳性Sperling指标，如图5所示。

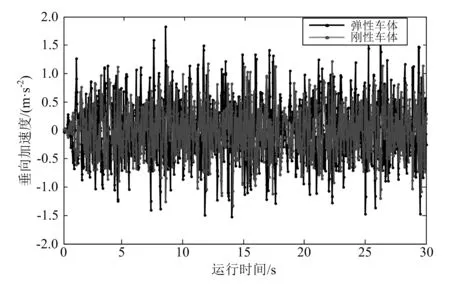
图4 车体垂向振动加速度

分析可知：相同工况下，弹性车体的振动加速度大于刚性车体的振动加速度；相同速度下，弹性车体的垂向和横向Sperling指标大于刚性车体，即刚性车体运行平稳性优于弹性车体；刚性车体和弹性车体的运行平稳性均随着速度的增加而减小，但在单轨最高限速90km/h内均满足运营要求，平稳性等级为“优”；弹性车体的平稳性曲线波动较大。因此，在寻求车体轻量化的同时，不可过分强调降低车体质量，以免车体刚度太小，运行平稳性变差。

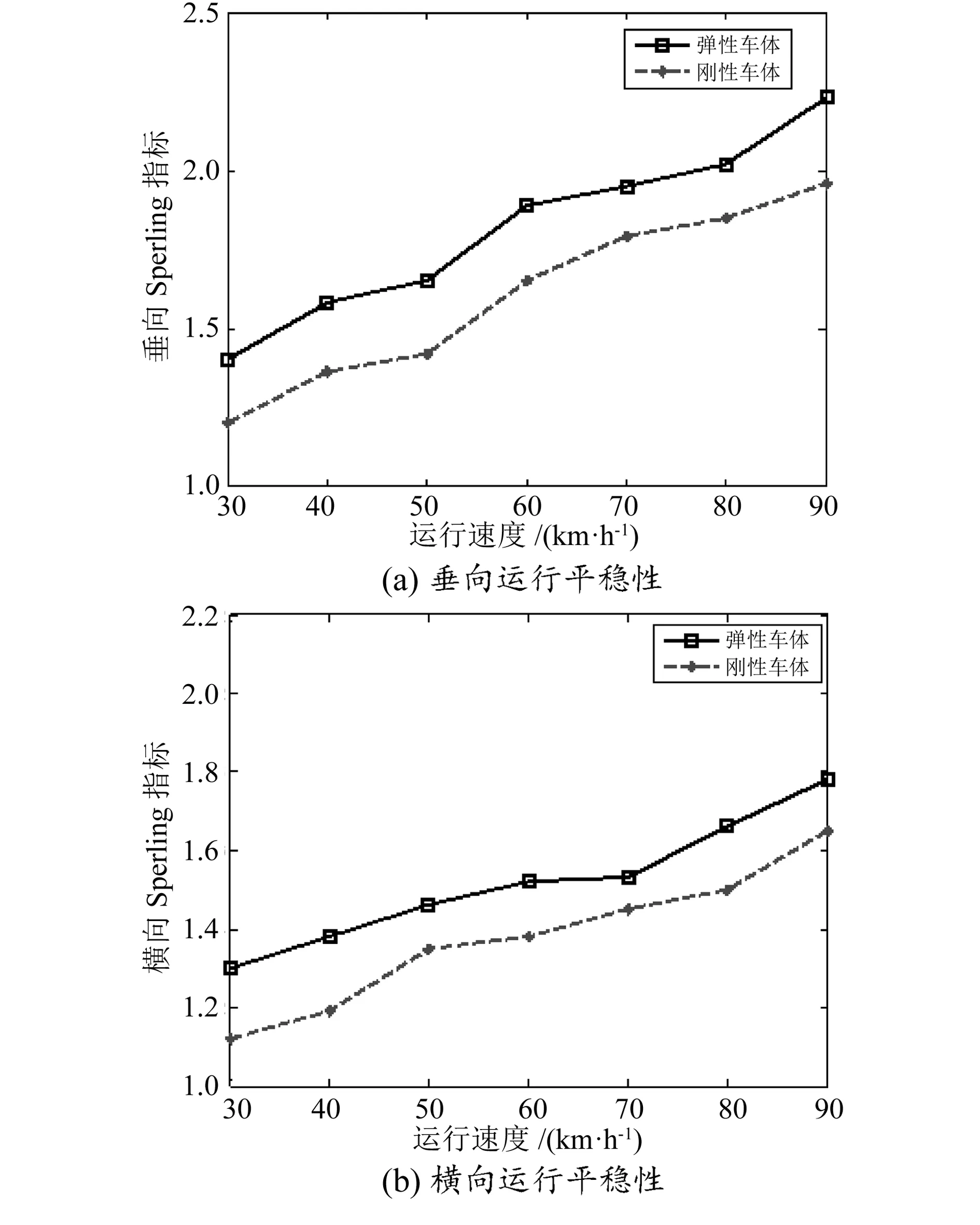
图5 不同运行速度下车辆运行平稳性

4 转向架与弹性车体垂向耦合振动分析

车体的弹性振动主要由转向架振动经二系悬挂装置传递产生，要确保车体运行的垂向动力学性能，必须考虑转向架与弹性车体的垂向耦合振动的运行特性，此时需要分析转向架浮沉与点头频率随一系悬挂垂向刚度变化的情况，研究转向架浮沉及点头频率对弹性车体运行平稳性的影响。因跨坐式单轨车体轴距较小或为单轴设计，转向架的点头和浮沉运动较铁道车辆更为明显，因此研究转向架浮沉及点头频率对弹性车体运行平稳性的影响至关重要。单轨转向架须安装抗点头装置，抑制构架的点头运动。抗点头装置的刚度对前后转向架同相和异相点头振动的影响如图6所示。随着抗点头装置刚度的增加，转向架的点头频率呈线性增大，阻尼比呈减小趋势；前后转向架同相点头时的频率大于异相点头频率，阻尼比呈大致相反趋势。

基于车辆刚柔耦合系统动力学模型，仿真分析在不同构架点头频率下车体的运行平稳性变化，如图7所示。

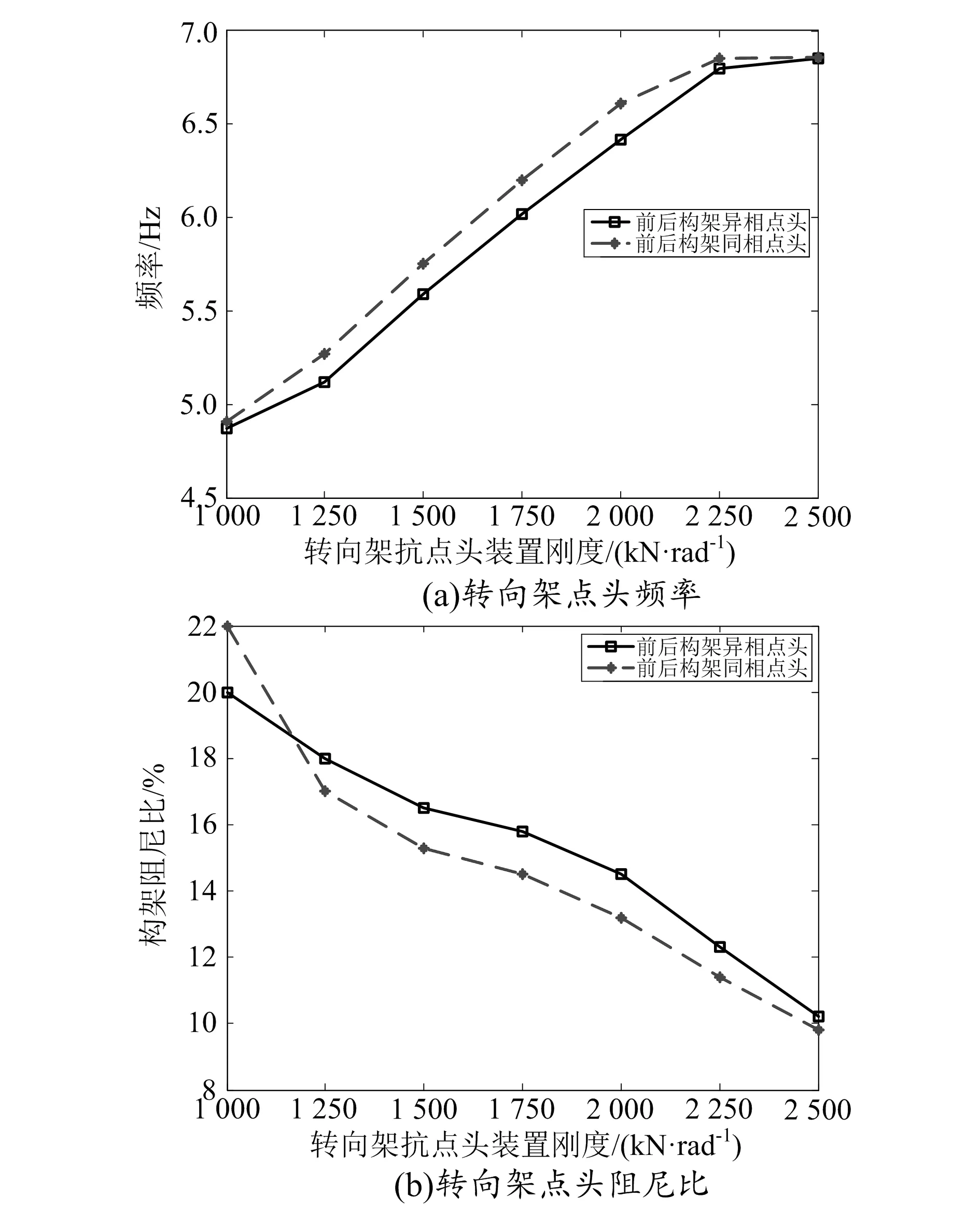
图6 前后转向架点头频率及阻尼比

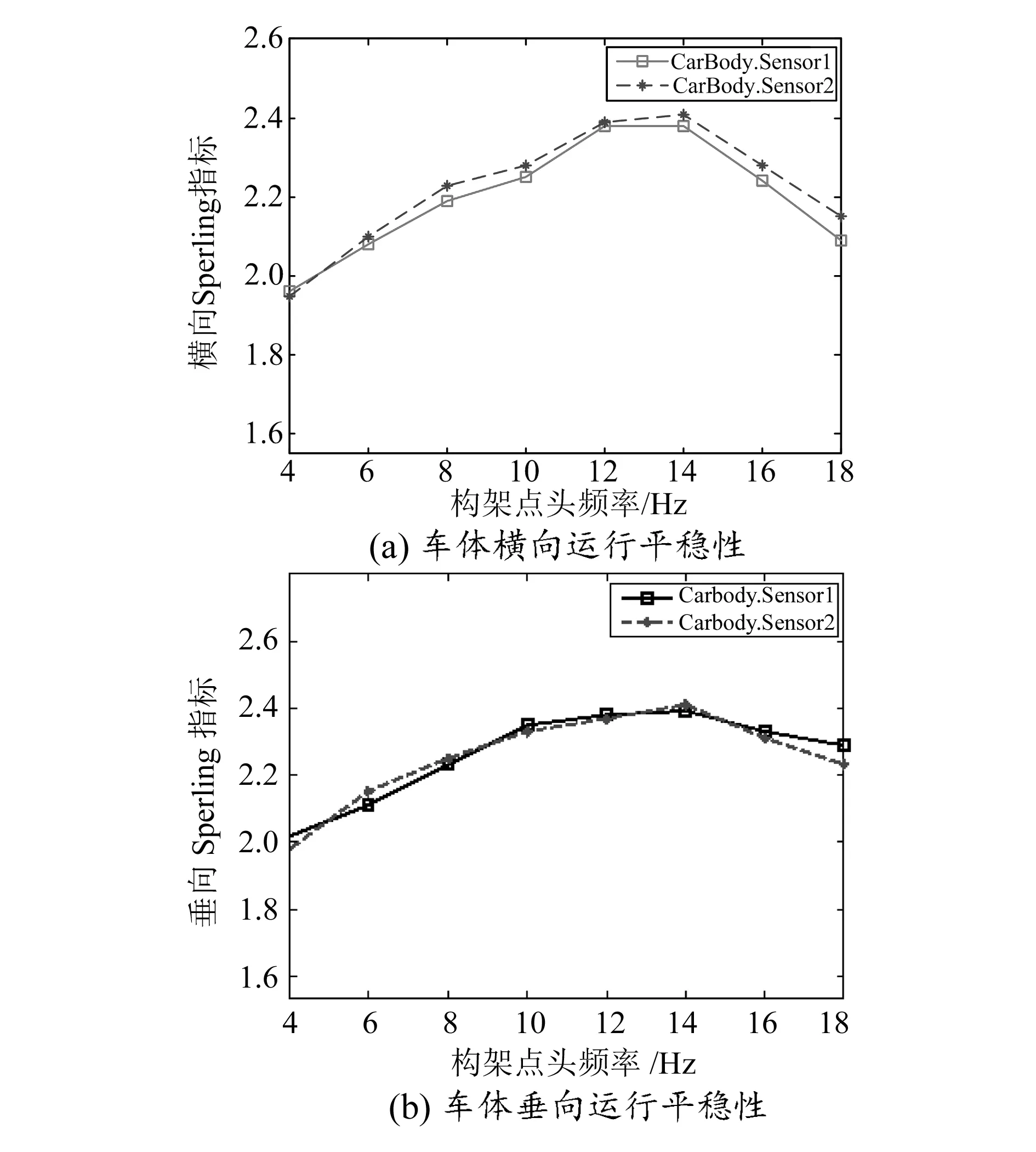
图7 不同构架点头频率下车体运行平稳性

由图7可知，转向架和弹性车体的耦合振动对车辆运行平稳性产生了不利影响。随着转向架点头频率(4～18Hz)的增加，垂向和横向平稳性的变化曲线均呈抛物线型，在转向架点头频率为12～14Hz时Sperling指数值达到最大，但最大值小于2.5，等级为“优”。 弹性车体模态计算中得到车体一阶垂弯频率为12.4Hz，此时转向架和弹性车体的耦合振动最为剧烈，车辆平稳性最低，但由于车辆悬挂系统参数的合理配置和阻尼力共同作用的效果，并未发生共振现象。空气弹簧和减振器安装在车体和构架间，是二系垂向悬挂装置，其作用是支撑车体和衰减振动。当转向架振动频率与车体的一阶垂弯频率一致时，垂向减振器阻尼系数和空气弹簧垂向刚度对车辆平稳性的影响如图8、图9所示。从图中可以看出，随着减振器阻尼系数增大，车辆平稳性迅速改善后又缓慢变差，阻尼系数在6 000N/(m·s-1)时车辆平稳性达到最优；车体平稳性随着空气弹簧刚度的减小而变好，即空气弹簧越“软”，车辆的平稳性越好。

图8 减振器阻尼值的影响

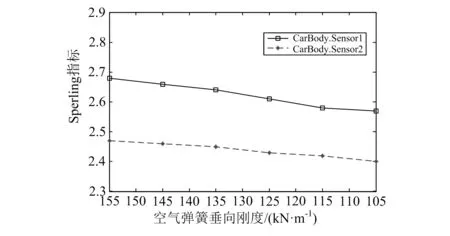
图9 空气弹簧刚度的影响

5 结论

本文对跨座式单轨弹性车体与转向架的耦合振动进行分析，得出以下结论：

1)相同运行速度下弹性车体比刚性车体运行平稳性差，波动更明显；随着速度增加，运行平稳性指标单调递增。

2)对于单轨车体车辆，随抗点头装置刚度的增加，转向架的点头频率呈线性增大，阻尼比呈减小趋势；前后转向架同相点头时的频率大于异相点头频率，阻尼比呈大致相反趋势。

3)只要跨座式单轨抗点头扭杆刚度、减振器阻尼系数和空气弹簧刚度与车体一阶弯曲频率匹配恰当，即使转向架点头频率和车体一阶弯曲频率相近，也不会发生弹性车体与转向架的共振。

4)随着减振器阻尼系数的增大，车辆的运行平稳性迅速改善后又缓慢变差，在阻尼系数为6 000N/(m·s-1)时平稳性达到最优。车体平稳性随着空气弹簧刚度减小而变好，即空气弹簧越“软”，车辆运行的平稳性越好。